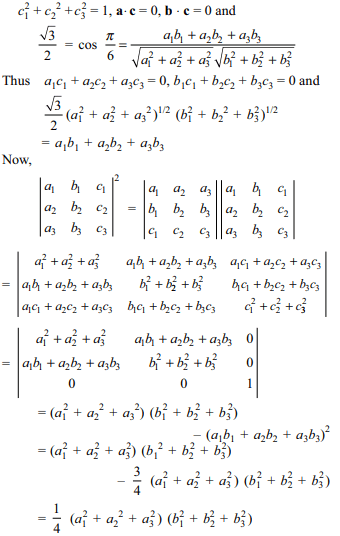1. Let A, B be two distinct points other than
the origin on the curve \[y=\frac{1}{2}x^{2}\] . Least value of area of \[\triangle OAB\] when OA . OB is minimum is
a) \[\sqrt{2}\]
b) 1
c) 2
d) \[\sqrt{3}\]
Explanation:
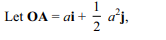
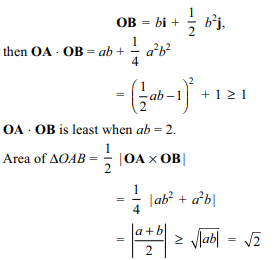
2. If a, b, c are three non-zero vectors, such
that
\[a \times b = b \times c = c \times a\] (1)
then
a) \[a=\frac{1}{2}\left(b+c\right)\]
b) a + b + c = 0
c) one of a, b, c must be unit vector
d) all three a, b, c must be unit vectors
Explanation: From (1), to get a, b, c are perpendicular to the same vector.
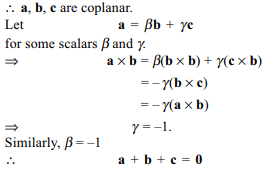
3. A vector c, directed along the internal bisector
of the angle between the vectors a = 7i – 4j – 4k and
b = –2i – j + 2k, with \[\mid c\mid=5\sqrt{6}\] , is
a) \[\frac{5}{3}\left(i-7j+2k\right)\]
b) \[\frac{5}{3}\left(5i+5j+2k\right)\]
c) \[\frac{5}{3}\left(i+7j+2k\right)\]
d) \[\frac{5}{3}\left(-5i+5j+2k\right)\]
Explanation: The required vector c is given by
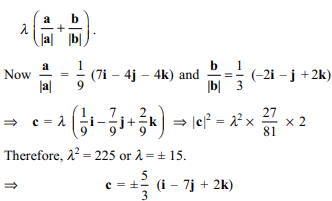
4. If \[d=a\times \left(b\times c \right)+b\times\left(c\times a\right)+c \times \left(a\times b\right)\] , then
a) d is a unit vector
b) d = a + b + c
c) d = 0
d) a, b c and d are coplanar
Explanation:
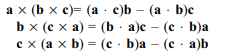
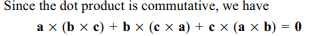
5. Let a = i + j + k, b = i – j + k and c = i –
j – k be three vectors. A vectors v in the plane of a and b,
whose projection on c is \[\frac{1}{\sqrt{3}}\] , is given by
a) i – 3j + 3k
b) – 3i – 3j – k
c) 3i – j + 3k
d) i + 3j – 3k
Explanation: As v lies in the plane of a and b, let v = \[\alpha\] a + \[\beta\] b, where \[\alpha\] , \[\beta\] \[\epsilon\] R
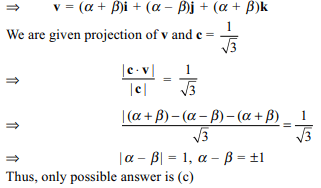
6. If p, q, r are three mutually perpendicular
vectors of the same magnitude and if a vector x
satisfied the equation \[p\times\left(\left(x-q\right)\times p\right)+q\times\left(\left(x-r\right)\times q\right)+r\times \left(\left(x-p\right)\times r\right)=0\]
then vector the x is
a) (1/2) (p + q – 2r)
b) (1/2) (p + q + r)
c) (1/3) (p + q + r)
d) (1/3) (2 p + q– r).
Explanation:
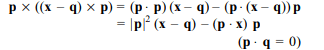
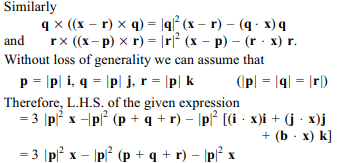
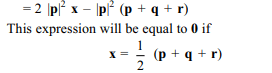
7. If a and b are two unit vectors, then the
vector \[\left(a+b\right)\times\left(a\times b\right)\] is parallel to the vector
a) a – b
b) a + b
c) 2a – b
d) 2a + b
Explanation:
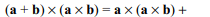
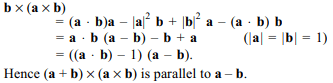
8. Let a = i + 2j + k, b = i – j + k and c =
i + j – k. A vector in the plane of a and b whose projection
on c is \[\frac{1}{\sqrt{3}}\] is
a) – 4i + j – 4k
b) 3i + j – 3k
c) i + j – 2k
d) 4i + j – 4k
Explanation: A vector d in the plane of a and b is of the form
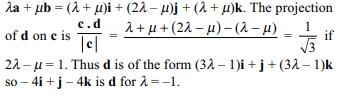
9. If \[a=\gamma\left(i+j-k\right), b=\mu\left(i-j+k\right)\] , and c
are unit vectors perpendicular to the vector a and coplanar
with a and b, then a unit vector d perpendicular to both a
and c is
a) \[\frac{1}{\sqrt{6}}\left(2i-j+k\right)\]
b) \[\frac{1}{\sqrt{2}}\left(j+k\right)\]
c) \[\frac{1}{\sqrt{6}}\left(i-2j+k\right)\]
d) \[\frac{1}{\sqrt{2}}\left(j-k\right)\]
Explanation: Let c = xi + yj + zk. Since a, b, c are coplanar
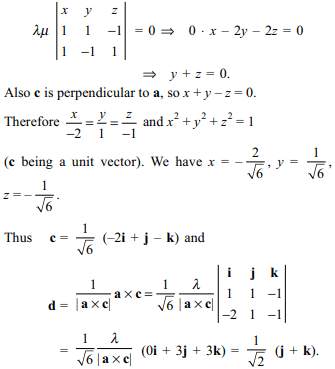
10. Let \[a=a_{1}i+a_{2}j+a_{3}k, b=b_{1}i+b_{2}j+b_{3}k\] and \[c=c_{1}i+c_{2}j+c_{3}k\] be three non-zero vectors such
that c is a unit vector perpendicular to both a and b. If the
angle between a and b is \[\pi/6\] , then \[\begin{bmatrix}a_{1} & a_{2} & a_{3}\\b_{1} & b_{2} & b_{3} \\c_{1} & c_{2} & c_{3} \end{bmatrix}^{2}\]
is equal to
a) 0
b) 1
c) \[\frac{1}{4}\left(a_1^2+a_2^2+a_3^2\right)\left(b_1^2+b_2^2+b_3^2\right)\]
d) \[\frac{3}{4}\left(a_1^2+a_2^2+a_3^2\right)\left(b_1^2+b_2^2+b_3^2\right)\left(c_1^2+c_2^2+c_3^2\right)\]
Explanation: