1. The apparent coefficient of expansion of a liquid when heated in a copper vessel is C and when heated in a silver vessel is S. If A is the linear coefficient of expansion of copper, then the linear
coefficient of expansion of silver is
a) \[\frac{C+S -3A}{3}\]
b) \[\frac{C+3A -S}{3}\]
c) \[\frac{S+3A -C}{3}\]
d) \[\frac{C+S +3A}{3}\]
Explanation:
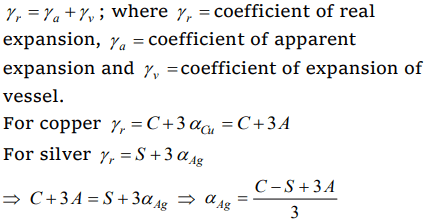
2. A uniform metal rod is used as a bar pendulum. If the room temperature rises by 10°C, and the coefficient of linear expansion of the metal of the rod is \[2\times10^{-6}\] per °C, the period of the pendulum
will have percentage increase of
a) \[-2\times10^{-3}\]
b) \[-1\times10^{-3}\]
c) \[2\times10^{-3}\]
d) \[1\times10^{-3}\]
Explanation:
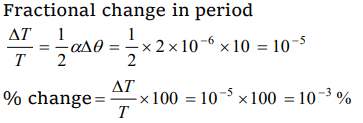
3. A bar of iron is 10 cm at 20°C. At 19°C it will be ( \[\alpha\] of iron= \[11\times10^{-6} \diagup ^{\circ} C\] )
a) \[11\times10^{-6}\] cm longer
b) \[11\times10^{-6}\] cm shorter
c) \[11\times10^{-5}\] cm shorter
d) \[11\times10^{-5}\] cm longer
Explanation:
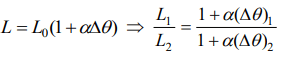
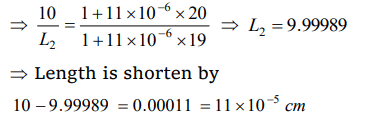
4. When a rod is heated but prevented from expanding, the stress developed is independent of
a) Material of the rod
b) Rise in temperature
c) Length of rod
d) None of above
Explanation: Stress = \[Y\alpha\triangle\theta\] ; hence it is independent of length.
5. Expansion during heating
a) Occurs only in solids
b) Increases the weight of a material
c) Decreases the density of a material
d) Occurs at the same rate for all liquids and solids
Explanation: Solids, liquids and gases all expand on being heated as result density (= mass/volume) decreases.
6. On heating a liquid of coefficient of cubical expansion \[\gamma\] in a container having coefficient of linear expansion \[\gamma\diagup3\], the level of liquid in the
container will
a) Rise
b) Fall
c) Will remain almost stationary
d) It is difficult to say
Explanation: As coefficient of cubical expansion of liquid equals coefficient of cubical expansion of vessel, the level of liquid will not change on heating
7. A pendulum clock keeps correct time at 0°C. Its mean coefficient of linear expansions is \[\alpha\diagup^{\circ}C\] , then the loss in seconds per day by the clock if the
temperature rises by t°C is
a) \[\frac{\frac{1}{2}\alpha t\times 864000}{1-\frac{\alpha t}{2}}\]
b) \[\frac{1}{2}\alpha t\times 864000\]
c) \[\frac{\frac{1}{2}\alpha t\times 864000}{\left(1-\frac{\alpha t}{2}\right)^{2}}\]
d) \[\frac{\frac{1}{2}\alpha t\times 864000}{1+\frac{\alpha t}{2}}\]
Explanation: Loss in time per second \[\frac{\triangle T}{T} = \frac{1}{2}\alpha\triangle \theta = \frac{1}{2}\alpha(t-0)\]
\[\Rightarrow\] loss in time per day
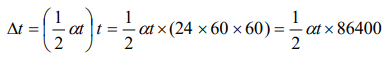
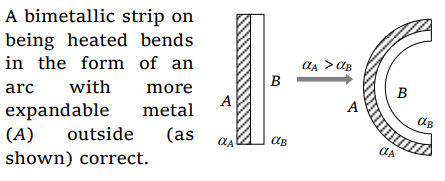
8. When a bimetallic strip is heated, it
a) Does not bend at all
b) Gets twisted in the form of an helix
c) Bend in the form of an arc with the more expandable metal outside
d) Bends in the form of an arc with the more expandable metal inside
Explanation:
9. A solid ball of metal has a concentric spherical cavity within it. If the ball is heated, the volume
of the cavity will
a) Increase
b) Decrease
c) Remain unaffected
d) None of these
Explanation: When the ball is heated, expansion of ball and cavity both occurs, hence volume of cavity increases
10. A litre of alcohol weighs
a) Less in winter than in summer
b) Less in summer than in winter
c) Some both in summer and winter
d) None of the above
Explanation: In summer alcohol expands, density decreases, so 1 litre of alcohol will weigh less in summer than in winter