1. A mercury drop of 1 cm radius is broken into 106 small drops. The energy used will be (surface tension of mercury is \[35\times10^{-3}N\diagup cm\] )
a) \[4.4 \times10^{-3}J\]
b) \[2.2 \times10^{-4}J\]
c) \[8.8 \times10^{-4}J\]
d) \[10^{4}J\]
Explanation:
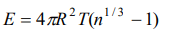
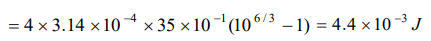
2. The surface tension of a liquid at its boiling point
a) Becomes zero
b) Becomes infinity
c) is equal to the value at room temperature
d) is half to the value at the room temperature
Explanation: Becomes zero
3. Surface tension of a soap solution is \[1.9\times10^{-2}N\diagup cm\] . Work done in blowing a bubble of 2.0 cm diameter will be
a) \[7.6\times10^{-6}joule\]
b) \[15.2\times10^{-6}joule\]
c) \[1.9\times10^{-6}joule\]
d) \[1\times10^{-4}joule\]
Explanation:
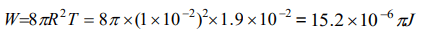
4. The surface tension of liquid is 0.5 N/m. If a film is held on a ring of area \[0.02 m^{2}\] , its surface energy is
a) \[5\times10^{-2}joule\]
b) \[2.0\times10^{-2}joule\]
c) \[4\times10^{-4}joule\]
d) \[0.8\times10^{-1}joule\]
Explanation:
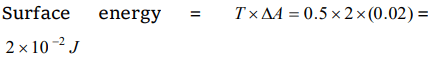
5. What is ratio of surface energy of 1 small drop and 1 large drop, if 1000 small drops combined to form 1 large drop
a) 100 : 1
b) 1000 : 1
c) 10 : 1
d) 1 : 100
Explanation:
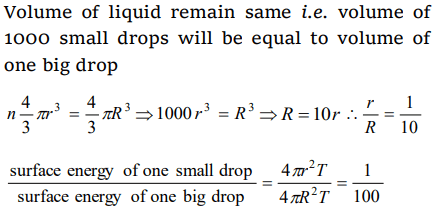
6. The work done in blowing a soap bubble of 10 cm radius is (Surface tension of the soap solution is \[\frac{3}{100} N\diagup m\] )
a) \[75.36\times10^{-4}joule\]
b) \[37.68\times10^{-4}joule\]
c) \[150.72\times10^{-4}joule\]
d) 75.36 joule
Explanation:
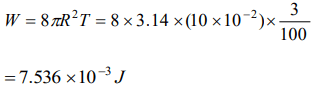
7. A liquid drop of diameter D breaks upto into 27 small drops of equal size. If the surface tension of the liquid is \[\sigma\], then change in surface energy is
a) \[\pi D^{2}\sigma\]
b) \[2\pi D^{2}\sigma\]
c) \[3\pi D^{2}\sigma\]
d) \[4\pi D^{2}\sigma\]
Explanation:
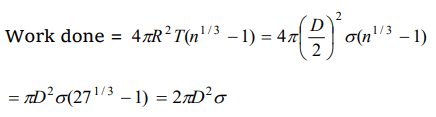
8.One thousand small water drops of equal radii combine to form a big drop. The ratio of final surface energy to the total initial surface energy
is
a) 1000 : 1
b) 1 : 1000
c) 10 : 1
d) 1 : 10
Explanation:
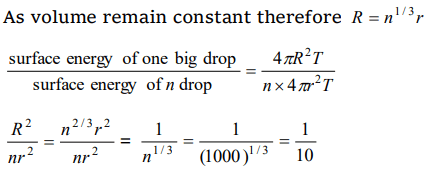
9. The work done in increasing the size of a soap film from 10 cm× 6 cm to 10 cm × 11 cm is \[3\times 10^{-4}joule\] . The surface tension of the film is
a) \[1.5\times 10^{-2}N\diagup m\]
b) \[3.0\times 10^{-2}N\diagup m\]
c) \[6.0\times 10^{-2}N\diagup m\]
d) \[11.0\times 10^{-2}N\diagup m\]
Explanation:
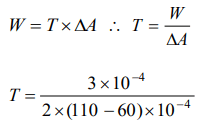
10. If \[\sigma\] be the surface tension, the work done in breaking a big drop of radius R in n drops of equal
radius is
a) \[Rn^{2/3}\sigma\]
b) \[\left(n^{2/3}-1\right)R\sigma\]
c) \[\left(n^{1/3}-1\right)R\sigma\]
d) \[4\pi R ^{2}\left(n^{1/3}-1\right)\sigma\]
Explanation: \[4\pi R ^{2}\left(n^{1/3}-1\right)\sigma\]