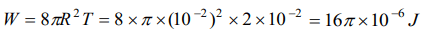1. Work done in splitting a drop of water of 1 mm radius into 106 droplets is (Surface tension of
water = \[72\times10^{-3} J\diagup m^{2}\] )
a) \[9.58\times10^{-5} J\]
b) \[8.95\times10^{-5} J\]
c) \[5.89\times10^{-5} J\]
d) \[5.98\times10^{-6} J\]
Explanation:
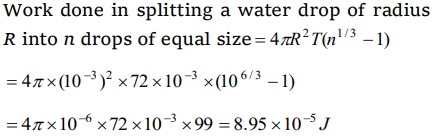
2. A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be
a) \[2\pi R^{2} T\]
b) \[3\pi R^{2} T\]
c) \[4\pi R^{2} T\]
d) \[2\pi R T^{2}\]
Explanation:
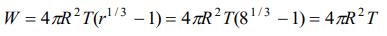
3. If T is the surface tension of soap solution, the amount of work done in blowing a soap bubble from a diameter D to 2D is
a) \[2\pi D^{2} T\]
b) \[4\pi D^{2} T\]
c) \[6\pi D^{2} T\]
d) \[8\pi D^{2} T\]
Explanation: Work done to increase the diameter of bubble from d to D
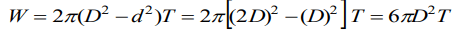
4. The radius of a soap bubble is increased from \[\frac{1}{\sqrt{\pi}} cm\] to \[\frac{2}{\sqrt{\pi}} cm\] . If the surface tension of water
is 30 dynes per cm, then the work done will be
a) 180 ergs
b) 360 ergs
c) 720 ergs
d) 960 ergs
Explanation:
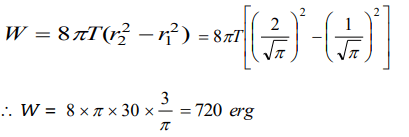
5. If work W is done in blowing a bubble of radius R from a soap solution, then the work done in blowing a bubble of radius 2R from the same
solution is
a) W/2
b) 2W
c) 4W
d) \[2\frac{1}{3} W\]
Explanation:
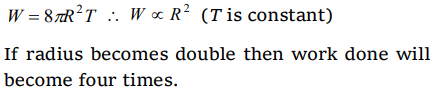
6. A spherical drop of oil of radius 1 cm is broken into 1000 droplets of equal radii. If the surface tension of oil is 50 dynes/cm, the work done is
a) \[18\pi\] ergs
b) \[180\pi\] ergs
c) \[1800\pi\] ergs
d) \[8000\pi\] ergs
Explanation:
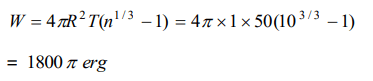
7. The work done in blowing a soap bubble of radius r of the solution of surface tension T will be
a) \[8\pi r^{2} T\]
b) \[2\pi r^{2} T\]
c) \[4\pi r^{2} T\]
d) \[\frac{4}{3}\pi r^{2} T\]
Explanation: \[8\pi r^{2} T\]
8. If two identical mercury drops are combined to form a single drop, then its temperature will
a) Decrease
b) Increase
c) Remains the same
d) None of the above
Explanation: Surface energy of combined drop will be lowered, so excess surface energy will raise the temperature of the drop
9.If the surface tension of a liquid is T, the gain in surface energy for an increase in liquid surface by A is
a) \[AT^{-1}\]
b) \[AT\]
c) \[A^{2}T\]
d) \[A^{2}T^{2}\]
Explanation: Surface energy = surface tension × increment in area
= T × A
10. The surface tension of a soap solution is \[2\times10^{-2}N\diagup m\] . To blow a bubble of radius 1 cm,
the work done is
a) \[4\pi\times10^{-6}J\]
b) \[8\pi\times10^{-6}J\]
c) \[12\pi\times10^{-6}J\]
d) \[16\pi\times10^{-6}J\]
Explanation: