1. A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?
a) 8 min 17 second
b) 10 min 57 second
c) 14 min 34 second
d) 12 min 23 second
Explanation:
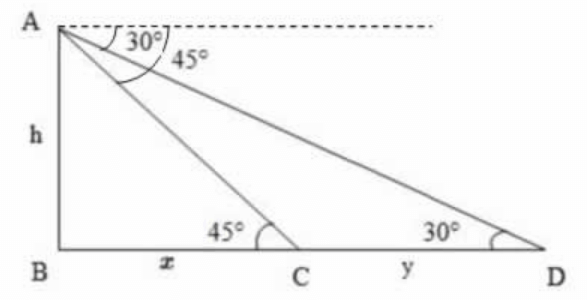
Consider the diagram shown above. Let AB be the tower. Let D and C be the positions of the car.
Then, ∠ ADC = 30° , ∠ ACB = 45°
Let AB = h, BC = x, CD = y
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{BC}} = \frac{h}{x} \cr & \Rightarrow 1 = \frac{h}{x} \cr & \Rightarrow h = x\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{AB}}{{\left( {BC + CD} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{h}{{x + y}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{{x + y}} \cr & x + y = \sqrt 3 \,h \cr & y = \sqrt 3 \,h - x \cr} $$
$$ y = \sqrt 3 \,h - h$$ ( Substituted the value of x from equation 1 )
$$ y = h\left( {\sqrt 3 - 1} \right)$$
Given that distance y is covered in 8 minutes.
i.e, distance $$h\left( {\sqrt 3 - 1} \right)$$ is covered in 8 minutes.
Time to travel distance x
= Time to travel distance h (∵ Since x = h as per equation 1).
Let distance h is covered in t minutes.
since distance is proportional to the time when the speed is constant, we have
$$\eqalign{ & h\left( {\sqrt 3 - 1} \right) \propto 8\,......\left( {\text{A}} \right) \cr & h \propto t\,..............\left( {\text{B}} \right) \cr & \frac{{\left( {\text{A}} \right)}}{{\left( {\text{B}} \right)}} \Rightarrow \frac{{h\left( {\sqrt 3 - 1} \right)}}{h} = \frac{8}{t} \cr & \Rightarrow \left( {\sqrt 3 - 1} \right) = \frac{8}{t} \cr & \Rightarrow t = \frac{8}{{\left( {\sqrt 3 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{\left( {1.73 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{.73}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{{800}}{{73}}\,{\text{minutes}} \cr & \,\,\,\,\,\,\,\,\,\,\, = 10\frac{{70}}{{73}}\,{\text{minutes}} \cr & \approx {\text{10}}\,{\text{minutes}}\,{\text{57}}\,{\text{seconds}} \cr} $$
2. Two vertical poles are 200 m apart and the height of one is double that of the other. From the middle point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary. Find the heights of the poles.
a) 141 m and 282 m
b) 70.5 m and 141 m
c) 65 m and 130 m
d) 130 m and 260 m
Explanation:
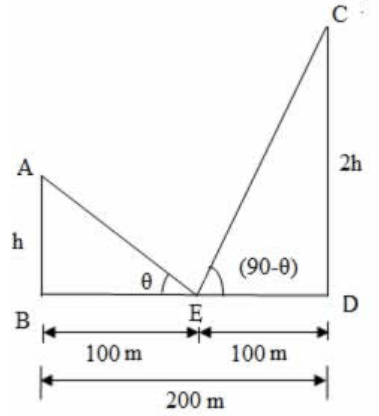
Let AB and CD be the poles with heights h and 2h respectively.
Given that distance between the poles, BD = 200 m
Let E be the middle point of BD,
∠ AEB = $$\theta $$
∠ CED = (90 - $$\theta $$) ( given that angular elevations are complementary)
Since E is the middle point of BD, we have BE = ED = 100 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \theta = \frac{{AB}}{{BE}} \cr & \tan \theta = \frac{h}{{100}} \cr & h = 100\tan \theta \,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta EDC, \cr & \tan\left( {90 - \theta } \right) = \frac{{CD}}{{ED}} \cr} $$
$$\cot \theta = \frac{{2h}}{{100}}$$ $$\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right]$$
$$\eqalign{ & 2h = 100\cot \theta \,......\left( 2 \right) \cr & \left( 1 \right) \times \left( 2 \right) \cr} $$
$$ \Rightarrow 2{h^2} = {100^2}$$ $$\left[ {\because \tan \theta \times \cot\theta = \tan\theta \times \frac{1}{{\tan \theta }} = 1} \right]$$
$$\eqalign{ & \Rightarrow \sqrt 2 \,h = 100 \cr & \Rightarrow h = \frac{{100}}{{\sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100 \times \sqrt 2 }}{{\sqrt 2 \times \sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50\sqrt 2 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50 \times 1.41 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 70.5 \cr & \Rightarrow 2h = 2 \times 70.5 = 141 \cr} $$
i.e. the height of the poles are 70.5 m and 141 m.
3. From the foot and the top of a building of height 230 m, a person observes the top of a tower with angles of elevation of b and a respectively. What is the distance between the top of these buildings if tan a = $$\frac{5}{{12}}$$ and tan b = $$\frac{4}{{5}}$$
a) 400 m
b) 250 m
c) 600 m
d) 650 m
Explanation:
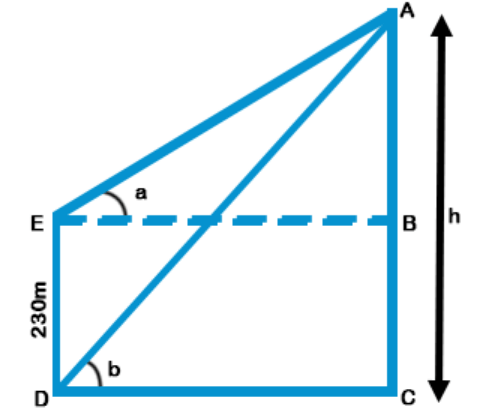
Let ED be the building and AC be the tower.
Given that ED = 230 m, ∠ADC = b, ∠AEB = a
Also given that tan a = $$\frac{5}{{12}}$$ and tan b = $$\frac{4}{{5}}$$
Let AC = h
Required Distance = Distance between the top of these buildings = AE
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \left( a \right) = \frac{{AB}}{{BE}} \cr} $$
$$ \Rightarrow \frac{5}{{12}} = \frac{{\left( {h - 230} \right)}}{{BE}}$$ [ tan(a) = $$\frac{5}{{12}}$$ (given), AB = (AC - BC) = (AC - ED) = (h - 230)]
$$\eqalign{ & \Rightarrow BE = \frac{{12\left( {h - 230} \right)}}{5}\,.....\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ACD, \cr & \tan \left( b \right) = \frac{{AC}}{{CD}} \cr} $$
$$ \Rightarrow \frac{4}{5} = \frac{h}{{CD}}$$ [ tan(b) = $$\frac{4}{5}$$ (given), AC = h]
$$\eqalign{ & \Rightarrow CD = \frac{{5h}}{4}\,.....\left( 2 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{diagram,}}\,BE = CD \cr} $$
$$ \Rightarrow \frac{{12\left( {h - 230} \right)}}{5} = \frac{{5h}}{4}$$ (from equation 1 & 2)
$$\eqalign{ & \Rightarrow 48h - \left( {4 \times 12 \times 230} \right) = 25h \cr & \Rightarrow 23h = \left( {4 \times 12 \times 230} \right) \cr & \Rightarrow h = \frac{{\left( {4 \times 12 \times 230} \right)}}{{23}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 480\,{\text{m}}\,......\left( 3 \right) \cr & AB = \left( {AC - BC} \right) \cr} $$
$$\,\,\,\,\,\,\,\,\,\,\,\, = \left( {480 - 230} \right)$$ [ Since AC = h = 480 (from 3) and BC = ED = 230 m(given)]
$$\,\,\,\,\,\,\,\,\,\,\,\, = 250\,{\text{m}}$$
In the triangle ABE, tan(a) =$$\frac{5}{{12}}$$ . Let's figure out the value of sin(a) now.
Consider a triangle with opposite side = 5 and adjacent side = 12 such that tan(a) = $$\frac{5}{{12}}$$
$$\eqalign{ & {\text{hypotenuse}} = \sqrt {{5^2} + {{12}^2}} = 13 \cr & {\text{i}}{\text{.e}}{\text{.,}} \cr & \sin \left( a \right) = \frac{{{\text{opposite}}\,{\text{side}}}}{{{\text{hypotenuse}}}} = \frac{5}{{13}} \cr} $$
We have seen that $$\sin \left( a \right) = \frac{5}{{13}}$$
$$\eqalign{ & \frac{{AB}}{{AE}} = \frac{5}{{13}} \cr & AE = AB \times \frac{{13}}{5} \cr & = 250 \times \frac{{13}}{5} \cr & = 650\,{\text{m}} \cr} $$
i.e., Distance between the top of the buildings = 650 m
4. From a tower of 80 m high, the angle of depression of a bus is 30°. How far is the bus from the tower?
a) 40 m
b) 138.4 m
c) 46.24 m
d) 160 m
Explanation:
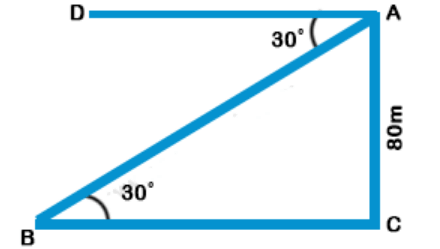
Let AC be the tower and B be the position of the bus.
Then BC = the distance of the bus from the foot of the tower.
Given that height of the tower, AC = 80 m and the angle of depression, ∠DAB = 30°
∠ABC = ∠DAB = 30° (because DA || BC)
$$\eqalign{ & \tan {30^ \circ } = \frac{{AC}}{{BC}} \cr & \tan {30^ \circ } = \frac{{80}}{{BC}} \cr & BC = \frac{{80}}{{\tan {{30}^ \circ }}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{80}}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}} \cr & = 80 \times 1.73 = 138.4\,{\text{m}} \cr} $$
i.e., Distance of the bus from the foot of the tower = 138.4 m
5. The elevation of the summit of a mountain from its foot is 45°. After ascending 2 km towards the mountain upon an incline of 30°,the elevation changes to 60°. What is the approximate height of the mountain?
a) 1.2 km
b) 0.6 km
c) 1.4 km
d) 2.7 km
Explanation:
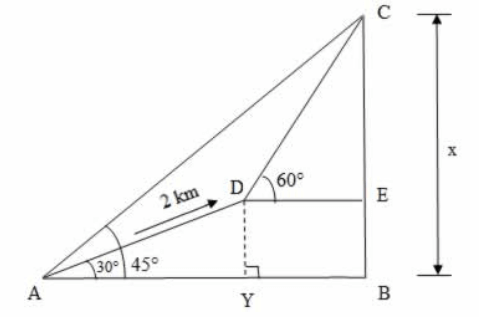
Let A be the foot and C be the summit of a mountain.
Given that ∠CAB = 45°
From the diagram, CB is the height of the mountain. Let CB = x
Let D be the point after ascending 2 km towards the mountain such that AD = 2 km and given that ∠DAY = 30°
It is also given that from the point D, the elevation is 60°
i.e., ∠CDE = 60°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC, \cr & \tan {45^ \circ } = \frac{{CB}}{{AB}} \cr} $$
$$ \Rightarrow 1 = \frac{x}{{AB}}$$ [ CB = x(the height of the mountain)]
$$\eqalign{ & \Rightarrow AB = x\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta AYD, \cr & \sin {30^ \circ } = \frac{{DY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{1}{2} = \frac{{DY}}{2}$$ ( Given that AD = 2)
$$\eqalign{ & \Rightarrow DY = 1\,.......\left( 2 \right) \cr & \cos {30^ \circ } = \frac{{AY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{AY}}{2}$$ ( Given that AD = 2)
$$\eqalign{ & \Rightarrow AY = \sqrt 3 \,......\left( 3 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta CED, \cr & \tan {60^ \circ } = \frac{{CE}}{{DE}} \cr} $$
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - EB} \right)}}{{YB}}$$ [ CE = (CB - EB) and DE = YB)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - DY} \right)}}{{AB - AY}}$$ [ EB = DY and YB = (AB - AY)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}}$$
[ CB = x, DY = 1(eq:2), AB = x(eq:1) and AY = $${\sqrt 3 }$$ (eq:3)]
$$\eqalign{ & \sqrt 3 = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}} \cr & x\sqrt 3 - 3 = x - 1 \cr & x\left( {\sqrt 3 - 1} \right) = 2 \cr & 0.73x = 2 \cr & x = \frac{2}{{0.73}} = 2.7 \cr} $$
6. If the height of a vertical pole is $$\sqrt 3 $$ times the length of its shadow on the ground, then the angle of elevation of the sun at that time is
a) 30°
b) 60°
c) 45°
d) 75°
Explanation: Let AB be a vertical pole and let its shadow be BC
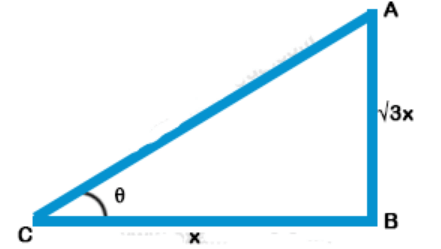
Let BC = x m, then length of pole = $$\sqrt 3 $$ x,
$$\theta $$ be the angle of elevation
$$\eqalign{ & {\text{tan}}\theta = \frac{{AB}}{{BC}} = \frac{{\sqrt 3 \,x}}{x} = \sqrt 3 \cr & = \tan {60^ \circ } \cr & \theta = {60^ \circ } \cr} $$
7. Two persons are 'a' meters apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is
a) $$\frac{a}{4}$$
b) $$\frac{a}{{\sqrt 2 }}$$
c) $$a\sqrt 2 $$
d) $$\frac{a}{{2\sqrt 2 }}$$
Explanation: Let AB and CD are two persons standing ‘a’ meters apart P is the mid-point of BD and from M, the angles of elevation of A and C are complementary
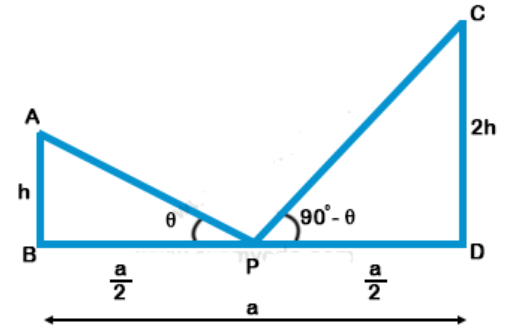
$$\eqalign{ & {\text{In}}\,\,\Delta {\text{APB,}} \cr & \tan \theta = \frac{{AB}}{{BP}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a} \cr & {\text{In}}\,\,\Delta {\text{CDP,}} \cr & \cot (90 - \theta ) = \frac{{PD}}{{CD}} = \frac{{\frac{a}{2}}}{{2h}} = \frac{a}{{4h}} \cr & {\text{We}}\,\,{\text{Know}}\,\,{\text{that,}} \cr & \tan \theta = \cot (90 - \theta ). \cr & \frac{{2h}}{a} = \frac{a}{{4h}} \cr & 8{h^2} = {a^2} \cr & h = \frac{a}{{2\sqrt 2 }} \cr} $$
8.If the angle of elevation of a tower from a distance of 100 metres from its foot is 60?, the height of the tower is
a) $$100\sqrt 3 \,m$$
b) $$\frac{{100}}{{\sqrt 3 }}\,m$$
c) $$50\sqrt 3 \,m$$
d) $$\frac{{200}}{{\sqrt 3 }}\,m$$
Explanation: Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°
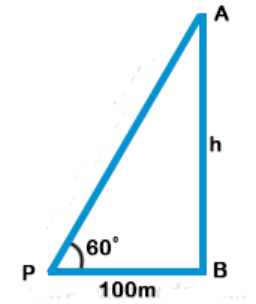
Let height of the tower = h
$$\eqalign{ & {\text{Then in right }}\Delta ABP \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {60^ \circ } = \frac{h}{{100}} \Rightarrow \sqrt 3 = \frac{h}{{100}} \cr & h = 100\sqrt 3 \cr & {\text{Height}}\,{\text{of}}\,{\text{tower}} = 100\sqrt 3 \cr} $$
9. The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart, the height of the light house is
a) $$\frac{{50}}{{\sqrt 3 + 1}}m$$
b) $$\frac{{50}}{{\sqrt 3 - 1}}m$$
c) $$50\left( {\sqrt 3 - 1} \right)m$$
d) $$50\left( {\sqrt 3 + 1} \right)m$$
Explanation: Let AB be the light house C and D are two ships whose angles of depression on A are 30° and 45° respectively
∠ACB = ∠XAC = 30° , ∠ADB = ∠YAD = 45° and
CD = 100m
Let AB =h and CB = x then BC = (100 - x)m
$$\eqalign{ & {\text{Now in }}\,\Delta ACB, \cr & \tan \theta = \frac{{AB}}{{CB}} \cr & \tan {30^ \circ } = \frac{h}{x} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{x} \cr & \Rightarrow x = \sqrt 3 h ......{\text{(i)}} \cr & {\text{Similarly in }}\,\Delta ADB \cr & \tan {45^ \circ } = \frac{{AB}}{{BD}} \cr & 1 = \frac{h}{{100 - x}} \cr & x = 100 - h \,......{\text{(ii)}} \cr & {\text{From (i) and (ii)}} \cr & \sqrt 3 h = 100 - h \cr & \Rightarrow (\sqrt 3 - 1)h = 100 \cr & h = \frac{{100}}{{\sqrt 3 + 1}} \cr & \,\,\,\,\,\, = \frac{{100\left( {\sqrt 3 - 1} \right)}}{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 - 1} \right)}} \cr & \,\,\,\,\,\, = \frac{{100\left( {\sqrt 3 - 1} \right)}}{{3 - 1}} \cr & \,\,\,\,\,\, = \frac{{100\left( {\sqrt 3 - 1} \right)}}{2} \cr & \,\,\,\,\,\, = 50\left( {\sqrt 3 - 1} \right) \cr} $$
height of light house $$ = 50\left( {\sqrt 3 - 1} \right)m$$
10. The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
a) 25 $$\sqrt 3 $$
b) 50 $$\sqrt 3 $$
c) 75 $$\sqrt 3 $$
d) 150
Explanation: AB is a tower and AB = 75 m
From A, the angle of depression of a car C
on the ground is 30°
$$\eqalign{ & {\text{Let distance }}BC = x \cr & {\text{Now in right }}\Delta ACB, \cr & \tan \theta = \frac{{AB}}{{BC}} \cr & \Rightarrow \tan {30^ \circ } = \frac{{75}}{x} \cr & \frac{1}{{\sqrt 3 }} = \frac{{75}}{x} \cr & x = 75\sqrt 3 \,m \cr & BC = 75\sqrt 3 \,m \cr} $$