1.A flagstaff is placed on top of a building. The flagstaff and building subtend equal angles at a point on level ground which is 200 m away from the foot of the building. If the height of the flagstaff is 50 m and the height of the building is h, which of the following is true?
a) h3 - 50h2 + (200)2h + (200)250 = 0
b) h3 - 50h2 - (200)2h + (200)250 = 0
c) h3 + 50h2 + (200)2h - (200)250 = 0
d) None of these
Explanation:
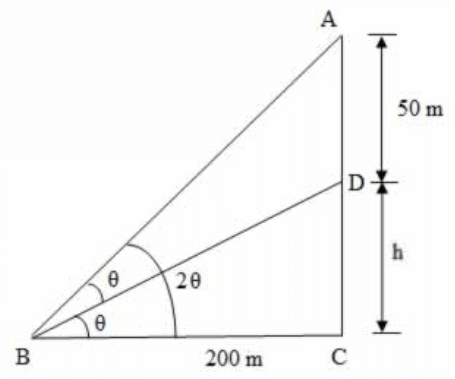
Let AD be the flagstaff and CD be the building.
Assume that the flagstaff and building subtend equal angles at point B.
Given that AD = 50 m, CD = h and BC = 200 m
Let ∠ABD = $$\theta $$, ∠DBC = $$\theta $$ ( flagstaff and building subtend equal angles at a point on level ground).
Then, ∠ABC = 2$$\theta $$
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta BCD, \cr & \tan \theta = \frac{{DC}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{h}{{200}}\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta BCA, \cr & \tan 2\theta = \frac{{AC}}{{BC}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{AD + DC}}{{200}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50 + h}}{{200}} \cr} $$
$$ \Rightarrow \frac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }} = \frac{{50 + h}}{{200}}$$ $$\left( {\because \tan \left( {2\theta } \right) = \frac{{2\tan \theta }}{{1 - {{\tan }^2}\theta }}} \right)$$
$$\frac{{2\left( {\frac{h}{{200}}} \right)}}{{1 - \frac{{{h^2}}}{{{{200}^2}}}}} = \frac{{50 + h}}{{200}}$$ ( substituted value of tan $$\theta $$ from eq:1)
$$\eqalign{ & 2h = \left( {1 - \frac{{{h^2}}}{{{{200}^2}}}} \right)\,\left( {50 + h} \right) \cr & 2h = 50 + h - \frac{{50{h^2}}}{{{{200}^2}}} - \frac{{{h^3}}}{{{{200}^2}}} \cr} $$
$$ 2\left( {{{200}^2}} \right)h = 50{\left( {200} \right)^2} + $$ $$h{\left( {200} \right)^2} - $$ $$50{h^2} - {h^3}$$
( multiplied LHS and RHS by $${{{200}^2}}$$ )
h3 + 50h2 + (200)2h - (200)250 = 0
2. From the top of a hill 100 m high, the angles of depression of the top and bottom of a pole are 30° and 60° respectively. What is the height of the pole
a) 52 m
b) 50 m
c) 66.67 m
d) 33.33 m
Explanation:
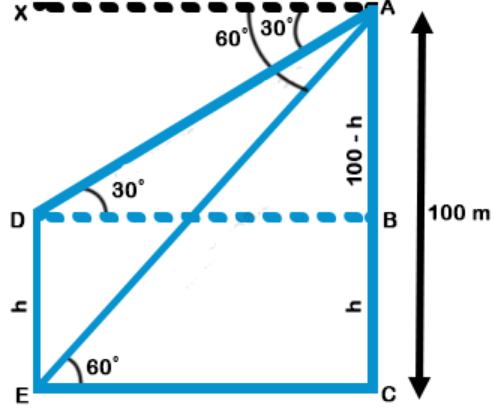
Consider the diagram shown above. AC represents the hill and DE represents the pole
Given that AC = 100 m
∠XAD = ∠ADB = 30° ( AX || BD )
∠XAE = ∠AEC = 60° ( AX || CE)
Let DE = h
Then, BC = DE = h,
AB = (100 - h) (∵ AC = 100 and BC = h),
BD = CE
$$\eqalign{ & \tan {60^ \circ } = \frac{{AC}}{{CE}} \cr & \sqrt 3 = \frac{{100}}{{CE}} \cr & CE = \frac{{100}}{{\sqrt 3 }}\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{BD}} \cr} $$
$$ \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{\left( {\frac{{100}}{{\sqrt 3 }}} \right)}}$$ ( BD = CE and substituted the value of CE from eq. 1)
$$\eqalign{ & \Rightarrow \left( {100 - h} \right) = \frac{1}{{\sqrt 3 }} \times \frac{{100}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100}}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 33.33 \cr & \Rightarrow h = 100 - 33.33 = 66.67\,{\text{m}} \cr} $$
i.e., the height of the pole = 66.67 m
3.A poster is on top of a building. Rajesh is standing on the ground at a distance of 50 m from the building. The angles of elevation to the top of the poster and bottom of the poster are 45° and 30° respectively. What is the height of the poster?
a) $$\frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right)$$
b) $$10\sqrt 3 \,{\text{m}}$$
c) $$50\sqrt 3 \,{\text{m}}$$
d) None of these
Explanation:
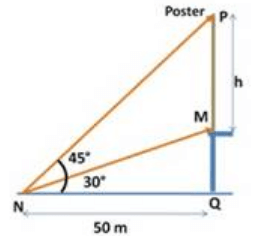
$$\eqalign{ & {\text{in}}\,\Delta PNQ,\,\tan {45^ \circ } = \frac{{PQ}}{{NQ}} \cr & PQ = NQ = 50{\text{m}} \cr & {\text{in}}\,\Delta MNQ,\,\tan {30^ \circ } = \frac{{MQ}}{{NQ}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{MQ}}{{50}} \cr & MQ = \frac{{50}}{{\sqrt 3 }} \cr & h = PM \cr & \,\,\,\,\,\,\,\,\,\, = PQ - MQ \cr & \,\,\,\,\,\,\,\,\,\, = 50 - \frac{{50}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right) \cr} $$
Poster height = $$\frac{{50}}{{\sqrt 3 }}\left( {\sqrt 3 - 1} \right)$$
4. Angles of elevation of pole are 60° and 45° from points at distances m and n on ground respectively. Here m, when measured from base of pole is less than n. What is the height of the pole?
a) $$\sqrt {mn\sqrt 3 } \,{\text{units}}$$
b) $$\sqrt {mn\root 4 \of 3 } \,{\text{units}}$$
c) $$\sqrt {3mn} \,{\text{units}}$$
d) $$\sqrt {mn} \,{\text{units}}$$
Explanation:
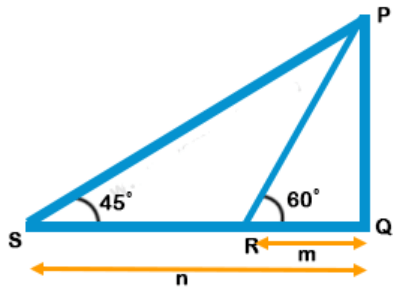
$$\eqalign{ & {\text{Height}}\,{\text{of}}\,{\text{pole}} = PQ \cr & \tan {60^ \circ } = \sqrt 3 = \frac{{PQ}}{m} \cr & \tan {45^ \circ } = 1 = \frac{{PQ}}{n} \cr & {\text{Multiply}}\,{\text{both}}\,{\text{equations}} \cr & \sqrt 3 \times 1 = \frac{{PQ}}{m} \times \frac{{PQ}}{n} \cr & PQ = \sqrt {mn\sqrt 3 } \,{\text{units}} \cr} $$
5. A tree is cut partially and made to fall on ground. The tree however does not fall completely and is still attached to its cut part. The tree top touches the ground at a point 10m from foot of the tree making an angle of 30°. What is the length of the tree?
a) $$10\sqrt 3 \,{\text{m}}$$
b) $$\frac{{10}}{{\sqrt 3 }}\,{\text{m}}$$
c) $$\frac{{\left( {\sqrt 2 - 1} \right)}}{{10}}\,{\text{m}}$$
d) $$\frac{{10}}{{\sqrt 2 }}\,{\text{m}}$$
Explanation:
$$\eqalign{ & {\text{in}}\,\Delta MNQ,\tan {30^ \circ } = \frac{{MQ}}{{NQ}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{MQ}}{{10}} \cr & MQ = \frac{{10}}{{\sqrt 3 }} \cr & {\text{Also}}\,{\text{by}}\,{\text{Pythagoras}}\,{\text{theorem}} \cr & M{N^2} = M{Q^2} + N{Q^2} \cr & {L^2} = \frac{{100}}{3} + 100 \cr & L = \frac{{20}}{{\sqrt 3 }} \cr & {\text{Height}}\,{\text{of}}\,{\text{tree}} = L + MQ \cr & = \frac{{20}}{{\sqrt 3 }} + \frac{{10}}{{\sqrt 3 }} \cr & = \frac{{30}}{{\sqrt 3 }} \cr & = \frac{{3 \times 10}}{{\sqrt 3 }} \cr & = 10\sqrt 3 \,{\text{m}} \cr} $$
6. The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electric pole and angle of elevation of 30° with the top of the pole. What is the height of electric pole ?
a) 5 meters
b) 8 meters
c) 10 meters
d) 12 meters
Explanation: Let AB be the tower and CD be the electric pole.
Then, $$\angle ACB = {60^ \circ },$$ $$\angle EDB = {30^ \circ }$$ and AB = 15 m
Let CD = h
Then, BE = (AB - AE) = (AB - CD) = (15 - h)
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan {60^ \circ } = \sqrt 3 \cr & \Rightarrow AC = \frac{{AB}}{{\sqrt 3 }} = \frac{{15}}{{\sqrt 3 }} \cr & {\text{And, }}\frac{{BE}}{{DE}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & DE = \left( {BE \times \sqrt 3 } \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt 3 \left( {15 - h} \right) \cr & {\text{So, }}AC = DE \cr & \frac{{15}}{{\sqrt 3 }} = \sqrt 3 \left( {15 - h} \right) \cr & 3h = \left( {45 - 15} \right) \cr & h = 10{\text{ m}} \cr} $$
7. TF is a tower with F on the ground. The angle of elevation of T from A is x° such that tan x°= $$\frac{2}{5}$$ and AF = 200 m. The angle of elevation of T from a nearer point B is y° with BF = 80 m. The value of y° is-
a) 75°
b) 45°
c) 60°
d) 30°
Explanation: $${\text{Given tan }}{x^ \circ } = \frac{2}{5}$$ and AF = 200 meter
$$\eqalign{ & \frac{2}{5} = \frac{{TF}}{{AF}} \cr & TF = \frac{{2 \times 200}}{5} \cr & TF = 80{\text{ m}} \cr & {\text{We have, BF = 80 m}} \cr & \tan {\text{ }}{y^ \circ } = \frac{{TF}}{{BF}} \cr & \tan {\text{ }}{y^ \circ } = \frac{{80}}{{80}} \cr & \tan {\text{ }}{y^ \circ } = 1 = \tan {45^ \circ } \cr & {y^ \circ } = {45^ \circ } \cr} $$
8. From the top of a tower, the angles of depression of two objects P and Q (situated on the ground on the same side of the tower) separated at a distance of 100$${\left( {3 - \sqrt 3 } \right)}$$ m are 45° and 60 ° respectively. The height of the tower is-
a) 200 m
b) 250 m
c) 300 m
d) None of these
Explanation:
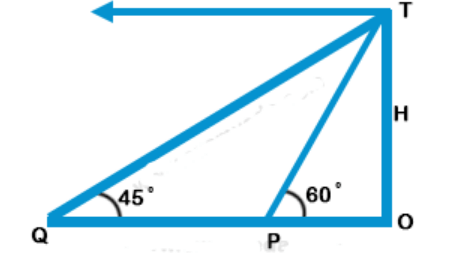
$$\eqalign{ & {\text{Let, }}OP = {\text{ }}a \cr & {\text{tan }}{60^ \circ } = \frac{H}{a} \cr & H = \sqrt 3 a \cr & \frac{H}{{\sqrt 3 }} = a.....(i) \cr} $$
$$tan{45^ \circ } = 1$$ $$ = \frac{H}{{a + 100\left( {3 - \sqrt 3 } \right)}}$$
$$ a + 100\left( {3 - \sqrt 3 } \right) = H$$
From (i) $$\frac{H}{{\sqrt 3 }} + $$ $$100\left( {3 - \sqrt 3 } \right)$$ = H
$$\eqalign{ & H + 300\sqrt 3 - 300 = \sqrt 3 H \cr & 300\sqrt 3 - 300 = \sqrt 3 H - H \cr & \left( {\sqrt 3 - 1} \right)H = 300\left( {\sqrt 3 - 1} \right) \cr & H = 300{\text{ m}} \cr} $$
9. From a lighthouse the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the lighthouse is h metres, the distance between the ships is
a) $$\left( {\sqrt 3 + 1} \right)\,h\,{\text{metres}}$$
b) $$\left( {\sqrt 3 - 1} \right)\,h\,{\text{metres}}$$
c) $$\sqrt 3 \,h\,{\text{metres}}$$
d) $${\text{1 + }}\left( {1 + \frac{1}{{\sqrt 3 }}} \right)\,h\,{\text{metres}}$$
Explanation: Let AB be lighthouse and P and Q are two ships on its opposite sides which form angle of elevation of A as 45° and 30° respectively AB = h
Let PB = x and QB = y
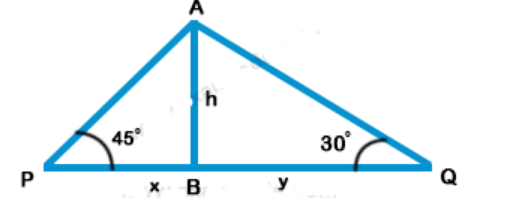
$$\eqalign{ & {\text{Now in right }}\Delta APB \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {45^ \circ } = \frac{h}{x} \Rightarrow 1 = \frac{h}{x} \cr & \Rightarrow x = h\,............(i) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan {30^ \circ } = \frac{{AP}}{{QB}} = \frac{h}{y} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{y} \cr & y = \sqrt 3 \,h\,..............(ii) \cr & {\text{Adding (i) and (ii)}} \cr & PQ = x + y \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = h + \sqrt 3 \,h \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {\sqrt 3 + 1} \right)\,h \cr} $$
10. If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
a) 1.5 m
b) 2 m
c) 2.5 m
d) 2.8 m
Explanation: Let AB is girls and CD is lamp-post AB = 1.5 which casts her shadow EB
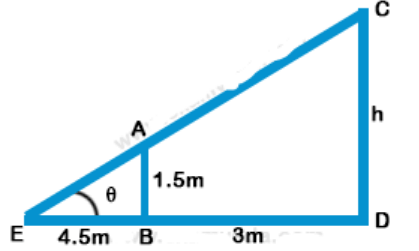
$$\eqalign{ & EB = 4.5\,m,\,BD = 3\,m \cr & {\text{Now in }}\Delta AEB \cr & \tan \theta = \frac{{AB}}{{BE}} = \frac{{1.5}}{{4.5}} = \frac{1}{3} \cr & {\text{and in }}\Delta CED \cr & \tan \theta = \frac{{CD}}{{ED}} \Rightarrow \frac{1}{3} = \frac{h}{{4.5 + 3}} \cr & \Rightarrow \frac{1}{3} = \frac{h}{{7.5}} \cr & \Rightarrow h = \frac{{7.5}}{3} - 2.5\,m \cr & {\text{Height of lamp - post}} = {\text{2}}{\text{.5}}\,m \cr} $$