1. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is: ages is:
a) 173 m
b) 200 m
c) 273 m
d) 300 m
Explanation: Let AB be the lighthouse and C and D be the positions of the ships.
Then, AB = 100m, ∠ACB = 30° and ∠ADB = 45°
$$\frac{{AB}}{{AC}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
$$ \Rightarrow AC = AB \times \sqrt 3 =100 \sqrt 3{\text{m}}$$
$$\frac{{AB}}{{AD}} = \tan {45^ \circ } = 1$$
$$ \Rightarrow AD = AB = 100{\text{m}}$$
CD = (AC+AD) = (100√3 +100)
= 100(√3 +1) = 100(1.73+1) =100 × 2.73 = 273m
2. A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?
a) 4 √3 units
b) 8 units
c) 12 units
d) Data inadequate
Explanation: One of AB, AD and CD must have given.
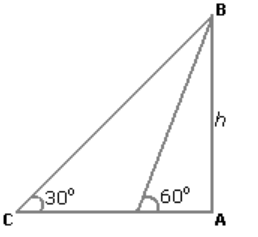
So, the data is inadequate.
3. The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:
a) 2.3 m
b) 4.6 m
c) 7.8 m
d) 9.2 m
Explanation: Let AB be the wall and BC be the ladder.
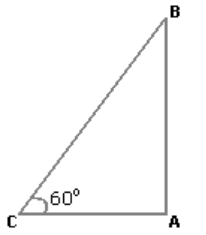
Then, ∠ACB = 60° = AC = 4.6m
$$\frac{{AC}}{{BC}} = \cos {60^ \circ } = \frac{1}{2}$$
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m
4. An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:
a) 21.6 m
b) 23.2 m
c) 24.72 m
d) None of these
Explanation: Let AB be the observer and CD be the tower.
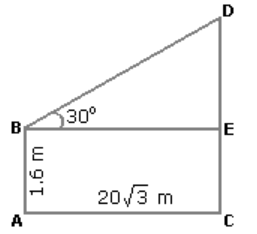
Draw BE ⊥ CD
Then CE = AB = 1.6m
BE = AC = 20√3m
$$\frac{{DE}}{{BE}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
$$ \Rightarrow DE = \frac{{BE}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{{\sqrt 3 }} = 20$$
CD = CE + DE = (1.6 + 20) m = 21.6 m
5.From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:
a) 149 m
b) 156 m
c) 173 m
d) 200 m
Explanation: Let AB be the tower
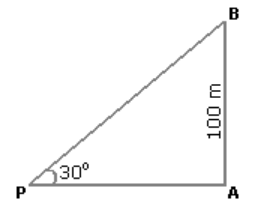
Then, ∠APB = 30° and AB = 100m
$$\frac{{AB}}{{AP}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
⇒ AP = AB × √3 = 100 × √3
AP = 100 × 1.73 = 173m
6. If the angles of elevation of a tower from two points distance a and b (a > b) from its foot and in the same straight line from it are 30° and 60°, then the height of the tower is?
a) $$\sqrt {a + b} $$
b) $$\sqrt {ab} $$
c) $$\sqrt {a - b} $$
d) $$\sqrt {\frac{a}{b}} $$
Explanation: Let AB be the tower and P and Q are such points that PB = a, QB = b and angles of elevation at P and Q are 30° and 60° respectively
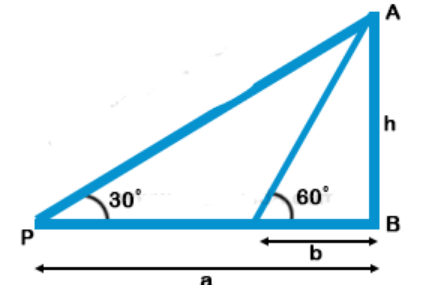
$$\eqalign{ & {\text{Let }}AB = h \cr & {\text{Now in right }}\Delta APB, \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {30^ \circ } = \frac{h}{a} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{a}\,...........(i) \cr & {\text{Similarly in right }}\Delta AQB, \cr & \tan {60^ \circ } = \frac{{AB}}{{QB}} \cr & \Rightarrow \sqrt 3 = \frac{h}{b}\,...........(ii) \cr & {\text{Multiplying (i) and (ii)}} \cr & \frac{1}{{\sqrt 3 }} \times \sqrt 3 = \frac{h}{a} \times \frac{h}{b} \cr & 1 = \frac{{{h^2}}}{{ab}} \cr & {h^2} = ab \cr & h = \sqrt {ab} \cr & {\text{Height of the tower}} = \sqrt {ab} \cr} $$
7. A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
a) $$15\sqrt 3 \,m$$
b) $$\frac{{15\sqrt 3 }}{2}\,m$$
c) $$\frac{{15}}{2}\,m$$
d) $$15\,m$$
Explanation: Let AB is a wall and AC is the ladder 15 m long which makes an angle of 60° with the ground
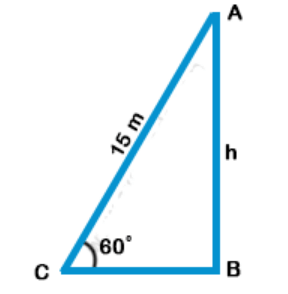
In ∆ABC, ∠B = 90°
Let height of wall AB = h
Then
$$\sin \theta = \frac{{AB}}{{AC}} \Rightarrow \sin {60^ \circ } = \frac{h}{{15}}$$
$$\eqalign{ & \frac{{\sqrt 3 }}{2} = \frac{h}{{15}} \cr & h = \frac{{15\sqrt 3 }}{2}\,m \cr} $$
Height of the wall $$ = \frac{{15\sqrt 3 }}{2}\,m $$
8. Two poles are ‘a’ metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
a) $$\sqrt {2a} \,{\text{metres}}$$
b) $$\frac{a}{{2\sqrt 2 }}\,{\text{metres}}$$
c) $$\frac{a}{{\sqrt 2 }}\,{\text{metres}}$$
d) $$2a\,{\text{metres}}$$
Explanation: Let height of pole CD = h
and AB = 2h, BD = a
M is mid-point of BD
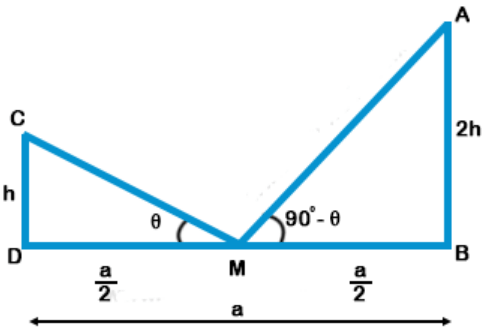
$$ DM = MB = \frac{a}{2}$$
$${\text{Let }}\angle CMD = \theta ,$$ $${\text{then }}\angle AMB = $$ $${90^ \circ } - \theta $$
$$\eqalign{ & \tan \theta = \frac{{CD}}{{DM}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a}\,......({\text{i}}) \cr & {\text{and}} \cr & tan\left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{MB}} = \frac{{2h}}{{\frac{a}{2}}} = \frac{{4h}}{a} \cr & \Rightarrow \cot \theta = \frac{{4h}}{a}\,..........({\text{ii}}) \cr & {\text{Multiplying (i) and (ii)}} \cr & {\text{tan}}\theta \times {\text{cot}}\theta = \frac{{2h}}{a} \times \frac{{4h}}{a} \cr & 1 = \frac{{8{h^2}}}{{{a^2}}} = {h^2} = \frac{{{a^2}}}{8}\,m \cr & h = \sqrt {\frac{{{a^2}}}{8}} = \frac{a}{{\sqrt 8 }} = \frac{a}{{2\sqrt 2 }}\,m \cr} $$
9. From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
a) 25 m
b) 50 m
c) 75 m
d) 100 m
Explanation: Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m
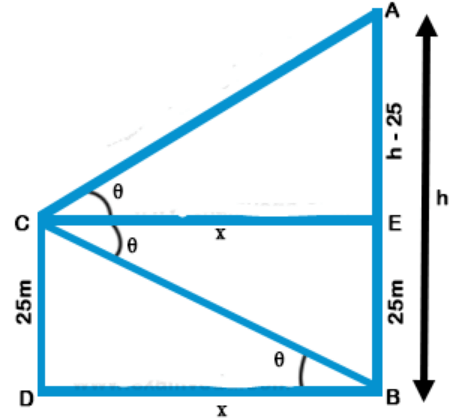
$$\eqalign{ & {\text{Let}}\,AB = h \cr & CE \,\, || \,\, DB \cr & EC = DB = x{\text{ }}\left( {{\text{suppose}}} \right) \cr & EB = CD = 25 \cr & AE = h - 25 \cr & {\text{Now in right }}\Delta CDB, \cr & \tan \theta = \frac{{CD}}{{DB}} = \frac{{25}}{x}\,......\left( {\text{i}} \right) \cr & {\text{and in right }}\Delta CAE \cr & \tan \theta = \frac{{AE}}{{CE}} = \frac{{h - 25}}{x}\,......\left( {{\text{ii}}} \right) \cr & {\text{From}}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) \cr & \frac{{25}}{x} = \frac{{h - 25}}{x} \cr & 25 = h - 25 \cr & h = 25 + 25 = 50 \cr & {\text{Height of tower}} = 50\,m \cr} $$
10. The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45°. Then the height of the tower (in metres) is
a) $$50\sqrt 3 $$
b) $$50$$
c) $$\frac{{50}}{{\sqrt 2 }}$$
d) $$\frac{{50}}{{\sqrt 3 }}$$
Explanation: Let AB be tower and C is a point on the ground 50 m away
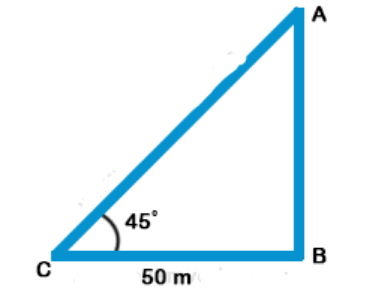
From foot of tower B
Angle of elevation is 45°
Let h be height of tower = x m
$$\eqalign{ & \tan \theta = \frac{{AB}}{{BC}} \cr & \tan {45^ \circ } = \frac{{AB}}{50} \cr & 1 = \frac{{AB}}{{50}} \Rightarrow AB = 50\,m \cr} $$