1.The ratio of the length of a rod and its shadow is 1 : $$\sqrt 3 $$ The angle of elevation of the sum is
a) 30°
b) 45°
c) 60°
d) 90°
Explanation: Let AB be rod and BC be its shadow
So that AB : BC = 1 : $$\sqrt 3 $$
Let $$\theta $$ be the angle of elevation
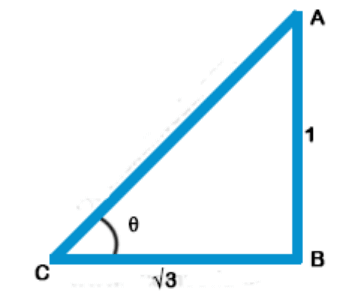
$$\eqalign{ & \tan \theta = \frac{{AB}}{{BC}} = \frac{1}{{\sqrt 3 }} = \tan {30^ \circ } \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {\because \tan {{30}^ \circ } = \frac{1}{{\sqrt 3 }}} \right) \cr & \theta = {30^ \circ } \cr} $$
Hence angle of elevation $$ = {30^ \circ }$$
2. It is found that on walking x metres towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60° . The height of the chimney is
a) $$3\sqrt 2 \,x$$
b) $$2\sqrt 3 \,x$$
c) $$\frac{{\sqrt 3 }}{2}\,x$$
d) $$\frac{2}{{\sqrt 3 }}\,x$$
Explanation: In the figure, AB is chimney and CB and DB are its shadow
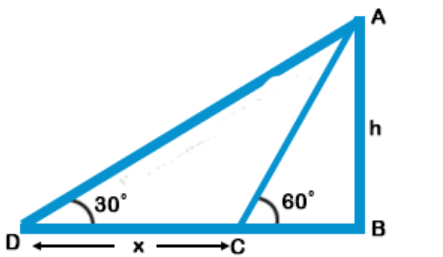
$$\eqalign{ & \tan {60^ \circ } = \frac{{AB}}{{BC}} = \frac{h}{{BC}} \cr & \sqrt 3 = \frac{h}{{BC}} \cr & \Rightarrow BC = \frac{h}{{\sqrt 3 }}\,.......\,\left( {\text{i}} \right) \cr & {\text{and}} \cr & \tan {30^ \circ } = \frac{h}{{DB}} = \frac{h}{{DB + BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{x + BC}} \cr & x + BC = h\sqrt 3 \cr & \Rightarrow BC = h\sqrt 3 - x\,.......\,\left( {{\text{ii}}} \right) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & \frac{h}{{\sqrt 3 }} = h\sqrt 3 - x \cr & \Rightarrow \frac{h}{{\sqrt 3 }} - h\sqrt 3 = - x \cr & x = h\sqrt 3 - \frac{h}{{\sqrt 3 }} \cr & x = h\left( {\sqrt 3 - \frac{1}{{\sqrt 3 }}} \right) \cr & x = h\frac{{3 - 1}}{{\sqrt 3 }} \cr & x = \frac{{2h}}{{\sqrt 3 }} \cr & h = \frac{{\sqrt 3 }}{2}x \cr} $$
3. A ladder makes an angle of 60° with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
a) $$\frac{4}{{\sqrt 3 }}$$
b) $$4\sqrt 3 $$
c) $$2\sqrt 2 $$
d) $$4$$
Explanation: Suppose AB is the ladder of length x m
OA = 2m, ∠OAB = 60°
$$\eqalign{ & {\text{In right }}\Delta AOB,\,\sec {60^ \circ } = \frac{x}{2} \cr & \Rightarrow 2 = \frac{x}{2} \cr & x = 4\,m \cr} $$
4. The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
a) 12 m
b) 10 m
c) 8 m
d) 6 m
Explanation: Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L
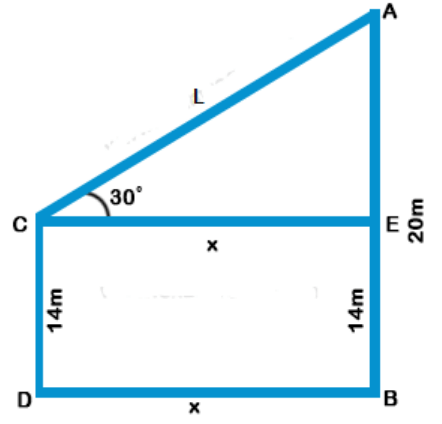
Now AE = AB - EB = AB - CD = 20 - 14 = 6 m
$$\eqalign{ & {\text{Now in right }}\Delta ACE, \cr & \sin \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} = \frac{{AE}}{{AC}} \cr & \sin {30^ \circ } = \frac{6}{{AC}} \cr & \frac{1}{2} = \frac{6}{{AC}} \cr & \Rightarrow AC = 2 \times 6 = 12 \cr & {\text{Length of AC}} = 12\,m \cr} $$
5. A lower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
a) $$\frac{h}{2}\,m$$
b) $$\sqrt 3 \,h\,m$$
c) $$\frac{h}{3}\,m$$
d) $$\frac{h}{{\sqrt 3 }}\,m$$
Explanation: Let CD is the tower and A is a point such that the angle of elevation of C is 30°
B is and their point h m high of A and angle of depression of D is 60°
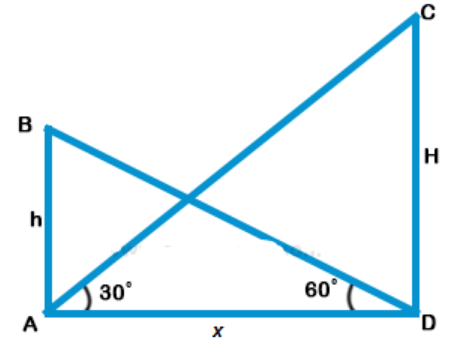
$$\eqalign{ & {\text{The}}\,AB = h\,m \cr & {\text{Let}}\,CD = H\,m\,\,\,{\text{and }}\,AD\, = x \cr & {\text{Now}}\,{\text{in}}\,{\text{right}}\,\Delta ABD, \cr & \tan \theta = \frac{{AB}}{{AD}} \cr & \tan {60^ \circ } = \frac{h}{x} \cr & \sqrt 3 = \frac{h}{x} \cr & \Rightarrow x = \frac{h}{{\sqrt 3 }}\,.......({\text{i}}) \cr & {\text{Similarly in right }}\Delta ACB, \cr & \tan {30^ \circ } = \frac{{CD}}{{AD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{H}{x} \cr & x = \sqrt 3 \,H\,.......\left( {{\text{ii}}} \right) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & \sqrt 3 \,H = \frac{h}{{\sqrt 3 }} \cr & H = \frac{h}{{\sqrt 3 \times \sqrt 3 }} = \frac{h}{3} \cr & {\text{Height of tower}} = \frac{h}{3} \cr} $$
6. An observer 2 m tall is $$10\sqrt 3 $$ m away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The height of the tower is:
a) 14 m
b) 12 m
c) 10 m
d) None of these
Explanation:
$$\eqalign{ & SR = PQ = 2\,m \cr & PS = QR = 10\sqrt 3 \,m \cr & \tan {30^ \circ } = \frac{{TS}}{{PS}} \cr & \frac{1}{{\sqrt 3 }} = \frac{{TS}}{{10\sqrt 3 }} \cr & TS = \frac{{10\sqrt 3 }}{{\sqrt 3 }} = 10\,m \cr & TR = TS + SR = 10 + 2 = 12\,m \cr} $$
7. A person, standing exactly midway between two towers, observes the top of the two towers at angle of elevation of 22.5° and 67.5°. What is the ratio of the height of the taller tower to the height of the shorter tower? (Given that tan 22.5° = $$\sqrt 2 - 1$$ )
a) $$1 - 2\sqrt 2 :1$$
b) $$1 + 2\sqrt 2 :1$$
c) $$3 + 2\sqrt 2 :1$$
d) $$3 - 2\sqrt 2 :1$$
Explanation:
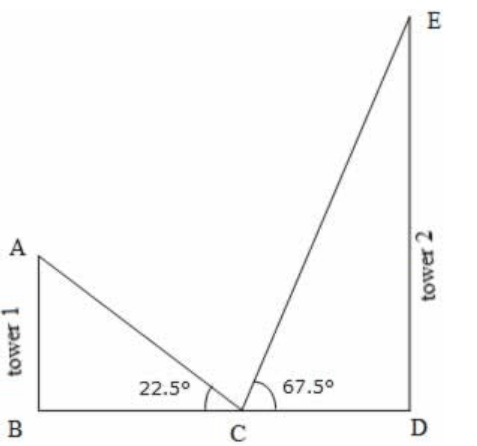
Let ED be the taller tower and AB be the shorter tower.
Let C be the point of observation
Given that ∠ ACB = 22.5° and ∠ DCE = 67.5°
Given that C is the midpoint of BD
Hence, BC = CD
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,ABC, \cr & \tan{22.5^ \circ } = \frac{{AB}}{{BC}}\,.....\left( {eq:1} \right)\, \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,CDE, \cr & \tan {67.5^ \circ } = \frac{{ED}}{{CD}}\,.....\left( {eq:2} \right) \cr & \frac{{\left( {eq:2} \right)}}{{\left( {eq:1} \right)}} \Rightarrow \frac{{\tan {{67.5}^ \circ }}}{{\tan{{22.5}^ \circ }}} = \frac{{\left( {\frac{{ED}}{{CD}}} \right)}}{{\left( {\frac{{AB}}{{BC}}\,} \right)}} \cr & = \frac{{ED}}{{AB}}\,\,\,\,\,\left( { CD = BC} \right) \cr & \Rightarrow \frac{{\tan \left( {{{90}^ \circ } - {{22.5}^ \circ }} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \Rightarrow \frac{{\cot {{22.5}^ \circ }}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right] \cr & \Rightarrow \frac{{\left( {\frac{1}{{\tan {{22.5}^ \circ }}}} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\,\left[ {\because \cot \theta = \frac{1}{{\tan \theta }}} \right] \cr & \Rightarrow \frac{{ED}}{{AB}} = \frac{1}{{{{\left( {\tan {{22.5}^ \circ }} \right)}^2}}} \cr & = \frac{1}{{{{\left( {\sqrt 2 - 1} \right)}^2}}} \cr & = {\left( {\frac{1}{{\sqrt 2 - 1}}} \right)^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {2 - 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{1}} \right]^2} \cr & = {\left( {\sqrt 2 + 1} \right)^2} \cr & = \left( {2 + 2\sqrt 2 + 1} \right) \cr & = \left( {3 + 2\sqrt 2 } \right) \cr & {\text{Required}}\,{\text{Ratio}} \cr & = ED:AB \cr & = \left( {3 + 2\sqrt 2 } \right):1 \cr} $$
8. A vertical tower stands on ground and is surmounted by a vertical flagpole of height 18 m. At a point on the ground, the angle of elevation of the bottom and the top of the flagpole are 30° and 60° respectively. What is the height of the tower
a) 9 m
b) 10.40 m
c) 15.57 m
d) 12 m
Explanation:
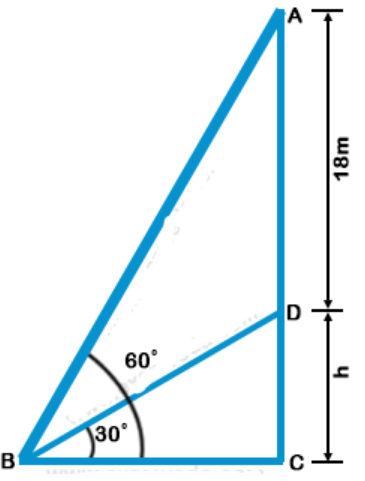
Let DC be the vertical tower and AD be the vertical flagpole. Let B be the point of observation.
Given that AD = 18 m, ∠ ABC = 60°, ∠ DBC = 30°
Let DC be h
$$\eqalign{ & \tan {30^ \circ } = \frac{{DC}}{{BC}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{BC}} \cr & h = \frac{{BC}}{{\sqrt 3 }}\,......\left( eq : 1 \right) \cr & \tan {60^ \circ } = \frac{{AC}}{{BC}} \cr & \sqrt 3 = \frac{{18 + h}}{{BC}} \cr & 18 + h = BC \times \sqrt 3 \,......\left( eq: 2 \right) \cr & \frac{eq : 1}{eq : 2} \Rightarrow \frac{h}{{18 + h}} = \frac{{\left( {\frac{{BC}}{{\sqrt 3 }}} \right)}}{{\left( {BC \times \sqrt 3 } \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{3} \cr & 3h = 18 + h \cr & 2h = 18 \cr & h = 9\,{\text{m}} \cr} $$
i.e., the height of the tower = 9 m
9. To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and he is 5 m away from the wall, what is the length of the window?
a) 8.65 m
b) 2 m
c) 2.5 m
d) 3.65 m
Explanation:
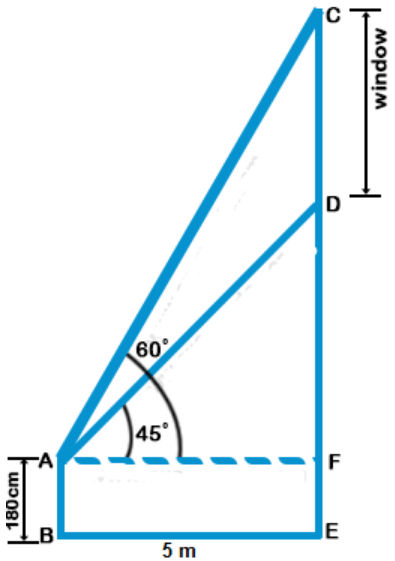
Let AB be the man and CD be the window
Given that the height of the man, AB = 180 cm, the distance between the man and the wall, BE = 5 m,
∠ DAF = 45°, ∠ CAF = 60°
From the diagram, AF = BE = 5 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFD, \cr & \tan {45^ \circ } = \frac{{DF}}{{AF}} \cr & 1 = \frac{{DF}}{5} \cr & DF = 5\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFC, \cr & \tan {60^ \circ } = \frac{{CF}}{{AF}} \cr & \sqrt 3 = \frac{{CF}}{5} \cr & CF = 5\sqrt 3 \,......\,\left( 2 \right) \cr & {\text{Length}}\,{\text{of}}\,{\text{the}}\,{\text{window}} \cr & = CD = \left( {CF - DF} \right) \cr} $$
$$ = 5\sqrt 3 - 5$$ [ Substituted the value of CF and DF from (1) and (2)]
$$\eqalign{ & = 5\left( {\sqrt 3 - 1} \right) \cr & = 5\left( {1.73 - 1} \right) \cr & = 5 \times 0.73 \cr & = 3.65\,{\text{m}} \cr} $$
10. When the sun's altitude changes from 30° to 60°, the length of the shadow of a tower decreases by 70m. What is the height of the tower?
a) 35 m
b) 140 m
c) 60.6 m
d) 20.2 m
Explanation:
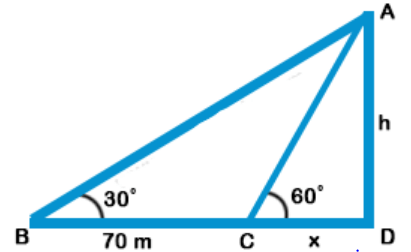
Let AD be the tower, BD be the initial shadow and CD be the final shadow.
Given that BC = 70 m, ∠ ABD = 30°, ∠ ACD = 60°,
Let CD = x, AD = h
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,CDA \cr & \tan {60^ \circ } = \frac{{AD}}{{CD}} \cr & \sqrt 3 = \frac{h}{x}\,......\left( {eq:1} \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,BDA \cr & \tan {30^ \circ } = \frac{{AD}}{{BD}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{70 + x}}\,......\left( {eq:2} \right) \cr & \frac{{eq:1}}{{eq:2}} \Rightarrow \frac{{\sqrt 3 }}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}} = \frac{{\left( {\frac{h}{x}} \right)}}{{\left( {\frac{h}{{70 + x}}} \right)}} \cr & \Rightarrow 3 = \frac{{70 + x}}{x} \cr & \Rightarrow 2x = 70 \cr & \Rightarrow x = 35 \cr} $$
Substituting this value of x in eq : 1, we have
$$\eqalign{ & \sqrt 3 = \frac{h}{{35}} \cr & \Rightarrow h = 35\sqrt 3 = 35 \times 1.73 \cr & = 60.55 \approx 60.6 \cr} $$