1. The dimension of quantity \[\left(L\diagup RCV\right)\] is
a) \[\left[A\right]\]
b) \[\left[A^{2}\right]\]
c) \[\left[A^{-1}\right]\]
d) None of these
Explanation:
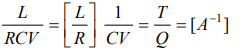
2. The dimension of the ratio of angular to linear momentum is
a) \[M^{0}L^{1}T^{0}\]
b) \[M^{1}L^{1}T^{-1}\]
c) \[M^{1}L^{2}T^{-1}\]
d) \[M^{-1}L^{-1}T^{-1}\]
Explanation:
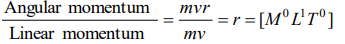
3. The pair having the same dimensions is
a) Angular momentum, work
b) Work, torque
c) Potential energy, linear momentum
d) Kinetic energy, velocity
Explanation: Dimension of work and torque = [ML2T-2]
4. The dimensions of surface tension are
a) \[ML^{-1}T^{-2}\]
b) \[MLT^{-2}\]
c) \[ML^{-1}T^{-1}\]
d) \[MT^{-2}\]
Explanation:
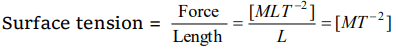
5. In the following list, the only pair which have different dimensions, is
a) Linear momentum and moment of a force
b) Planck's constant and angular momentum
c) Pressure and modulus of elasticity
d) Torque and potential energy
Explanation: Linear momentum = Mass * Velocity =[MLT-1]
Moment of a force = Force * Distance = [ML2T-2]
6. If R and L represent respectively resistance and self inductance, which of the following combinations has the dimensions of frequency:
a) \[\frac{R}{L}\]
b)\[\frac{L}{R}\]
c) \[\sqrt{\frac{R}{L}}\]
d) \[\sqrt{\frac{L}{R}}\]
Explanation:
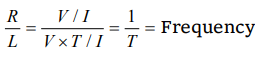
7. If velocity v , acceleration A and force F are chosen as fundamental quantities, then the dimensional formula of angular momentum in
terms of v, A and F would be
a) \[FA^{-1}v\]
b) \[Fv^{3}A^{-2}\]
c) \[Fv^{2}A^{-1}\]
d) \[F^{2}v^{2}A^{-1}\]
Explanation:
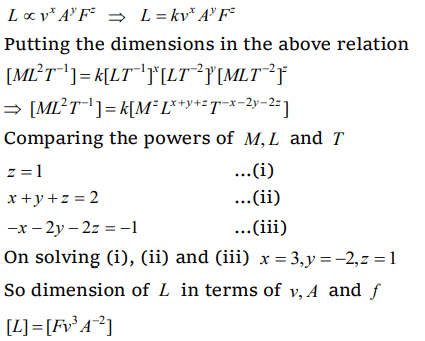
8. The dimensions of permittivity \[\epsilon_{0}\] are
a) \[A^{2}T^{2}M^{-1}L^{-3}\]
b) \[A^{2}T^{4}M^{-1}L^{-3}\]
c) \[A^{-2}T^{-4}ML^{3}\]
d) \[A^{2}T^{-4}M^{-1}L^{-3}\]
Explanation:
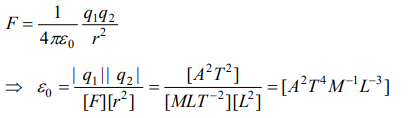
9. Dimensions of the following three quantities are
the same
a) Work, energy, force
b) Velocity, momentum, impulse
c) Potential energy, kinetic energy, momentum
d) Pressure, stress, coefficient of elasticity
Explanation: [Pressure] = [Stress] = [coefficient of elasticity] = [ML-1T-2]
10. The dimensions of Planck's constant and angular momentum are respectively
a) \[ML^{2}T^{-1}\] and \[MLT^{-1} \]
b) \[ML^{2}T^{-1}\] and \[ML^{2}T^{-1} \]
c) \[MLT^{-1}\] and \[ML^{2}T^{-1} \]
d) \[MLT^{-1}\] and \[ML^{2}T^{-2} \]
Explanation: \[ML^{2}T^{-1}\] and \[ML^{2}T^{-1} \]