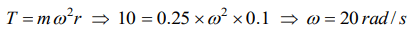1. A particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance 'r' . The speed of the
particle is
a) Proportional to \[r^{2}\]
b) Independent of r
c) Proportional to r
d) Proportional to\[\frac{1}{r}\]
Explanation:
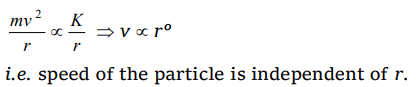
2. Two masses M and m are attached to a vertical axis by weightless threads of combined length l . They are set in rotational motion in a horizontal
plane about this axis with constant angular velocity \[\omega\] . If the tensions in the threads are the same during motion, the distance of M from the axis is
a) \[\frac{Ml}{M+m}\]
b) \[\frac{ml}{M+m}\]
c) \[\frac{M+m}{M}l\]
d) \[\frac{M+m}{m}l\]
Explanation:
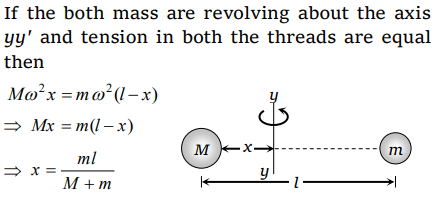
3. A boy on a cycle pedals around a circle of 20 metres radius at a speed of 20 metres/sec. The combined mass of the boy and the cycle is 90 kg.
The angle that the cycle makes with the vertical so that it may not fall is \[\left(g=9.8 m\diagup sec^{2}\right)\]
a) \[60.25^{\circ}\]
b) \[63.90^{\circ}\]
c) \[26.12^{\circ}\]
d) \[30.00^{\circ}\]
Explanation:
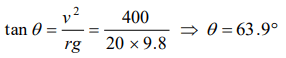
4. The average acceleration vector for a particle having a uniform circular motion is
a) A constant vector of magnitud\[\frac{v^{2}}{r}\]
b) A vector of magnitude \[\frac{v^{2}}{r}\] directed normal to the plane of the given uniform circular motion
c) Equal to the instantaneous acceleration vector at the start of the motion
d) A null vector
Explanation: In complete revolution change in velocity becomes zero so average acceleration will be zero
5. Radius of the curved road on national highway is R . Width of the road is b . The outer edge of the road is raised by h with respect to inner edge so
that a car with velocity v can pass safe over it. The value of h is
a) \[\frac{v^{2}b}{Rg}\]
b) \[\frac{v}{Rgb}\]
c) \[\frac{v^{2}R}{g}\]
d) \[\frac{v^{2}b}{R}\]
Explanation:
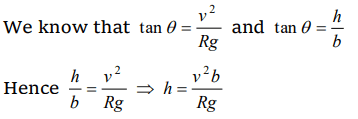
6. When a particle moves in a uniform circular motion. It has
a) Radial velocity and radial acceleration
b) Tangential velocity and radial acceleration
c) Tangential velocity and tangential acceleration
d) Radial velocity and tangential acceleration
Explanation: Tangential velocity and radial acceleration
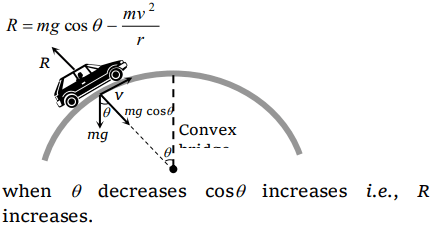
7. A motorcycle is going on an overbridge of radius R . The driver maintains a constant speed. As the motorcycle is ascending on the overbridge, the
normal force on it
a) Increases
b) Decreases
c) Remains the same
d) Fluctuates
Explanation:
8. A mass of 2 kg is whirled in a horizontal circle by means of a string at an initial speed of 5 revolutions per minute. Keeping the radius constant the tension in the string is doubled. The new speed is nearly
a) 14 rpm
b) 10 rpm
c) 2.25 rpm
d) 7 rpm
Explanation:
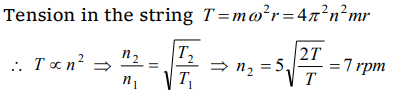
9. The magnitude of the centripetal force acting on a body of mass m executing uniform motion in a circle of radius r with speed v is
a) mvr
b) \[mv^{2}\diagup r\]
c) \[v\diagup r^{2}m\]
d) \[v\diagup r m\]
Explanation: \[mv^{2}\diagup r\]
10. A string breaks if its tension exceeds 10 newtons.
A stone of mass 250 gm tied to this string of
length 10 cm is rotated in a horizontal circle. The
maximum angular velocity of rotation can be
a) 20 rad/s
b) 40 rad/s
c) 100 rad/s
d) 200 rad/s
Explanation: