1. A car is moving with high velocity when it has a turn. A force acts on it outwardly because of
a) Centripetal force
b) Centrifugal force
c) Gravitational force
d) All the above
Explanation: Centrifugal force
2. A motor cycle driver doubles its velocity when he is having a turn. The force exerted outwardly will be
a) Double
b) Half
c) 4 times
d) \[\frac{1}{4} times\]
Explanation:
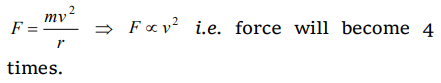
3. The coefficient of friction between the tyres and the road is 0.25. The maximum speed with which a car can be driven round a curve of radius 40 m
without skidding is \[\left(g =10ms^{-2}\right)\]
a) \[40ms^{-1}\]
b) \[20ms^{-1}\]
c) \[15ms^{-1}\]
d) \[10ms^{-1}\]
Explanation:
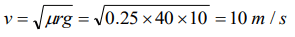
4. An athlete completes one round of a circular track of radius 10 m in 40 sec. The distance covered by him in 2 min 20 sec is
a) 70 m
b) 140 m
c) 110 m
d) 220 m
Explanation:
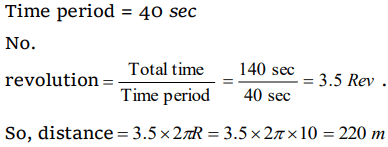
5. A proton of mass \[1.6\times10^{-27}kg\] goes round in a circular orbit of radius 0.10 m under a centripetal force of \[4\times10^{-13}N\] . then the frequency of
revolution of the proton is about
a) \[0.08\times10^{8}\] cycles per sec
b) \[4\times10^{8}\] cycles per sec
c) \[8\times10^{8}\] cycles per sec
d) \[12\times10^{8}\] cycles per sec
Explanation:
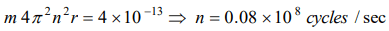
6. A particle is moving in a circle with uniform speed v. In moving from a point to another diametrically opposite point
a) The momentum changes by mv
b) The momentum changes by 2mv
c) The kinetic energy changes by \[\left(1\diagup 2\right)mv^{2}\]
d) The kinetic energy changes by \[mv^{2}\]
Explanation: Momentum changes by 2mv but kinetic energy remains same
7. In uniform circular motion
a) Both the angular velocity and the angular momentum vary
b) The angular velocity varies but the angular momentum remains constant
c) Both the angular velocity and the angular momentum stay constant
d) The angular momentum varies but the angular velocity remains constant
Explanation: L = I \[\omega\]
In U.C.M. \[\omega\] = constant, L = constant
8. When a body moves in a circular path, no work is done by the force since
a) There is no displacement
b) There is no net force
c) Force and displacement are perpendicular to each other
d) The force is always away from the centre
Explanation: W = FS cos \[\theta\]
\[\theta\] = 90°
9. Which of the following statements is false for a particle moving in a circle with a constant angular speed
a) The velocity vector is tangent to the circle
b) The acceleration vector is tangent to the circle
c) The acceleration vector points to the centre of the circle
d) The velocity and acceleration vectors are perpendicular to each other
Explanation: The acceleration vector is tangent to the circle
10. If \[a_{r}\] and \[a_{t}\] represent radial and tangential accelerations, the motion of a particle will be uniformly circular if
a) \[a_{r}=0\] and \[a_{t}=0\]
b) \[a_{r}=0\] but \[a_{t}\neq0\]
c) \[a_{r}\neq0\] but \[a_{t}=0\]
d) \[a_{r}\neq0\] and \[a_{t}\neq0\]
Explanation: In uniform circular motion tangential acceleration remains zero but magnitude of radial acceleration remains constant