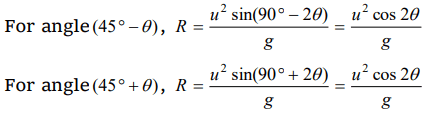1. A ball is thrown upwards and it returns to ground describing a parabolic path. Which of the following remains constant
a) Kinetic energy of the ball
b) Speed of the ball
c) Horizontal component of velocity
d) Vertical component of velocity
Explanation: Because there is no accelerating or retarding force available in horizontal motion.
2. At the top of the trajectory of a projectile, the directions of its velocity and acceleration are
a) Perpendicular to each other
b) Parallel to each other
c) Inclined to each other at an angle of \[45^{\circ}\]
d) Antiparallel to each other
Explanation: Direction of velocity is always tangent to the path so at the top of trajectory, it is in horizontal direction and acceleration due to gravity is always in vertically downward direction. It means angle between \[\overrightarrow{v}\] and \[\overrightarrow{g}\] are perpendicular to each other.
3. An object is thrown along a direction inclined at an angle of \[45^{\circ}\] with the horizontal direction. The horizontal range of the particle is equal to
a) Vertical height
b) Twice the vertical height
c) Thrice the vertical height
d) Four times the vertical height
Explanation:

4. The height y and the distance x along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by \[y=\left(8t-5t^{2}\right)\] meter and \[x=6t\] meter, where t is in
second. The velocity with which the projectile is projected is
a) 8 m/sec
b) 6 m/sec
c) 10 m/sec
d) Not obtainable from the data
Explanation:
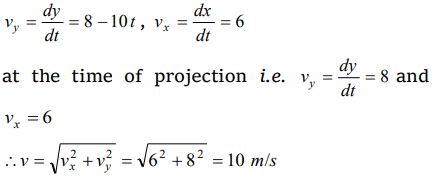
5. The height y and the distance x along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by \[y=\left(8t-5t^{2}\right)\] meter and \[x=6t\] meter, where t is in
second. The angle with the horizontal at which the projectile was projected is
a) \[\tan^{-1}\left(3\diagup4\right)\]
b) \[\tan^{-1}\left(4\diagup3\right)\]
c) \[\sin^{-1}\left(3\diagup4\right)\]
d) Not obtainable from the data
Explanation:
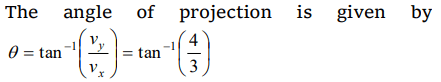
6. The height y and the distance x along the horizontal plane of a projectile on a certain planet (with no surrounding atmosphere) are given by \[y=\left(8t-5t^{2}\right)\] meter and \[x=6t\] meter, where t is in
second. The acceleration due to gravity is given by
a) \[10 m\diagup sec^{2}\]
b) \[5 m\diagup sec^{2}\]
c) \[20 m\diagup sec^{2}\]
d) \[2.5 m\diagup sec^{2}\]
Explanation:
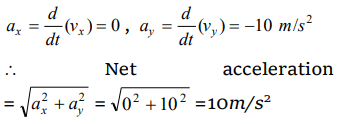
7. The range of a particle when launched at an angle of \[15^{\circ}\] with the horizontal is 1.5 km. What is the
range of the projectile when launched at an angle of \[45^{\circ}\] to the horizontal
a) 1.5 km
b) 3.0 km
c) 6.0 km
d) 0.75 km
Explanation:
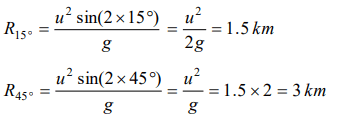
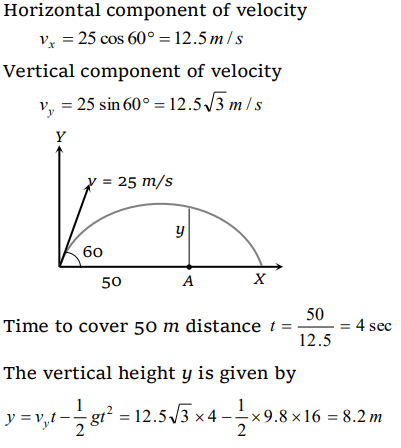
8. A cricketer hits a ball with a velocity 25 m / s at \[60^{\circ}\] above the horizontal. How far above the ground it passes over a fielder 50 m from the bat
(assume the ball is struck very close to the ground)
a) 8.2 m
b) 9.0 m
c) 11.6 m
d) 12.7 m
Explanation:
9. A stone is projected from the ground with velocity 25 m / s . Two seconds later, it just clears a wall 5m high. The angle of projection of the stone is \[\left(g=10m\diagup s^{2}\right)\]
a) \[30^{\circ}\]
b) \[45^{\circ}\]
c) \[50.2^{\circ}\]
d) \[60^{\circ}\]
Explanation:
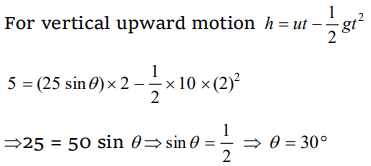
10. Galileo writes that for angles of projection of a projectile at angles \[\left(45+\theta\right)\] and \[\left(45-\theta\right)\] , the horizontal ranges described by the projectile are
in the ratio of if \[\left(\theta\leq45\right)\]
a) 2 : 1
b) 1 : 2
c) 1 : 1
d) 2 : 3
Explanation: