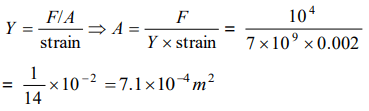1.To double the length of a iron wire having \[0.5 cm^{2}\] area of cross-section, the required force will be
\[\left(Y=10^{12}dyne\diagup cm^{2}\right)\]
a) \[1.0\times10^{-7}N\]
b) \[1.0\times10^{7}N\]
c) \[0.5\times10^{-7}N\]
d) \[0.5\times10^{12}dyne\]
Explanation:
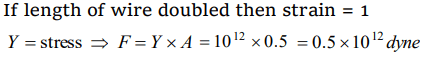
2.The spring balance does not read properly after its long use, because
a) The elasticity of spring increases
b) The elasticity decreases
c) Its plastic power decreases
d) Its plastic power increases
Explanation: Due to elastic fatigue its elastic property decreases.
3.Two wires of equal lengths are made of the same material. Wire A has a diameter that is twice as
that of wire B. If identical weights are suspended from the ends of these wires, the increase in length is
a) Four times for wire A as for wire B
b) Twice for wire A as for wire B
c) Half for wire A as for wire B
d) One-fourth for wire A as for wire B
Explanation:
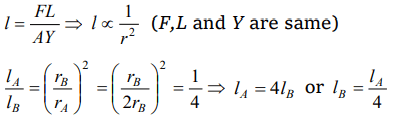
4.Why the spring is made up of steel in comparison of copper
a) Copper is more costly than steel
b) Copper is more elastic than steel
c) Steel is more elastic than Copper
d) None of the above
Explanation: Steel is more elastic than Copper
5. Steel and copper wires of same length are stretched by the same weight one after the other. Young's modulus of steel and copper are
\[2\times10^{11} N\diagup m^{2} \] and \[1.2\times10^{11} N\diagup m^{2} \] . The ratio of increase in length
a) \[\frac{2}{5}\]
b) \[\frac{3}{5}\]
c) \[\frac{5}{4}\]
d) \[\frac{5}{2}\]
Explanation:
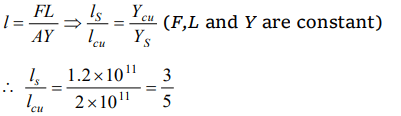
6. An area of cross-section of rubber string is \[ 2cm^{2} \] . Its length is doubled when stretched with a linear
force of \[ 2\times10^{5} dynes\] . The Young's modulus of the rubber in \[dynes\diagup cm^{2} \] will be
a) \[4\times10^{5} \]
b) \[1\times10^{5} \]
c) \[2\times10^{5} \]
d) \[1\times10^{4} \]
Explanation:
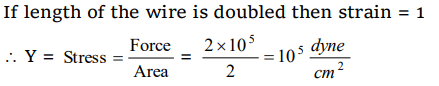
7. Increase in length of a wire is 1 mm when suspended by a weight. If the same weight is suspended on a wire of double its length and double its radius, the increase in length will be
a) 2 mm
b) 0.5 mm
c) 4 mm
d) 0.25 mm
Explanation:
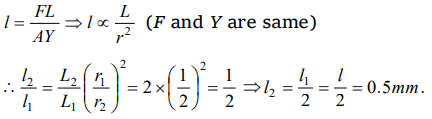
8. The temperature of a wire of length 1 metre and area of cross-section \[1 cm^{2} \] is increased from 0°C to 100°C. If the rod is not allowed to increase in
length, the force required will be\[\left(\alpha=10^{-5} \diagup^{\circ}C , Y=10^{11} N\diagup m^{2}\right)\]
a) \[10^{3} N\]
b) \[10^{4} N\]
c) \[10^{5} N\]
d) \[10^{9} N\]
Explanation:
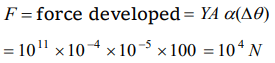
9.A rod of length l and area of cross-section A is heated from 0°C to 100°C. The rod is so placed
that it is not allowed to increase in length, then the force developed is proportional to
a) l
b) \[l^{-1} \]
c) A
d) \[A^{-1} \]
Explanation:
10. An aluminum rod ( Young's modulus \[=7\times10^{9} N\diagup m^{2} \] ) has a breaking strain of 0.2%. The
minimum cross-sectional area of the rod in order
to support a load of 104 Newton's is
a) \[1\times10^{-2} m^{2}\]
b) \[1.4\times10^{-3} m^{2}\]
c) \[3.5\times10^{-3} m^{2}\]
d) \[7.1\times10^{-4} m^{2}\]
Explanation: