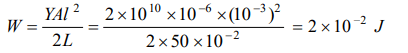1. The ratio of Young's modulus of the material of
two wires is 2 : 3. If the same stress is applied on
both, then the ratio of elastic energy per unit
volume will be
a) 3 : 2
b) 2 : 3
c) 3 : 4
d) 4 : 3
Explanation:
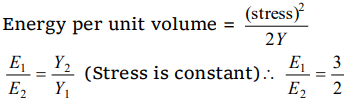
2. The length of a rod is 20 cm and area of crosssection \[2c m^{2}\] . The Young's modulus of the material of wire is \[1.4\times 10^{11}N\diagup m^{2}\] . If the rod is compressed by 5 kg-wt along its length, then
increase in the energy of the rod in joules will be
a) \[8.57\times 10^{-6}\]
b) \[22.5\times 10^{-4}\]
c) \[9.8\times 10^{-5}\]
d) \[45.0\times 10^{-5}\]
Explanation:
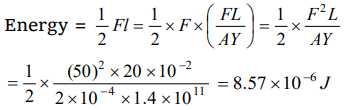
3. If a spring extends by x on loading, then the
energy stored by the spring is (if T is tension in
the spring and k is spring constant)
a) \[\frac{T^{2}}{2x}\]
b) \[\frac{T^{2}}{2k}\]
c) \[\frac{2x}{T^{2}}\]
d) \[\frac{2T^{2}}{k}\]
Explanation:
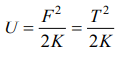
4.On stretching a wire, the elastic energy stored per
unit volume is
a) \[Fl\diagup 2AL\]
b) \[FA\diagup 2L\]
c) \[FL\diagup 2A\]
d) \[FL\diagup 2\]
Explanation:
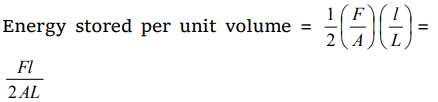
5. When a force is applied on a wire of uniform
cross-sectional area \[3\times 10^{-6}m^{2}\] and length 4m, the
increase in length is 1 mm. Energy stored in it will
be \[\left(Y=2\times 10^{11}N\diagup m^{2}\right)\]
a) 6250 J
b) 0.177 J
c) 0.075 J
d) 0.150 J
Explanation:
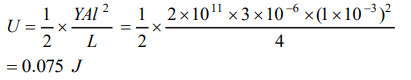
6. K is the force constant of a spring. The work done
in increasing its extension from \[l_{1}\] to\[l_{2}\] will be
a) \[K\left(l_{2}-l_{1}\right)\]
b) \[\frac{K}{2}\left(l_{2}+l_{1}\right)\]
c) \[K\left(l_2^2-l_1^2\right)\]
d) \[\frac{K}{2}\left(l_2^2-l_1^2\right)\]
Explanation:

7. When a 4 kg mass is hung vertically on a light
spring that obeys Hooke's law, the spring
stretches by 2 cms. The work required to be done
by an external agent in stretching this spring by 5
cms will be \[\left(g= 9.8 m \diagup sec^{2}\right)\]
a) 4.900 joule
b) 2.450 joule
c) 0.495 joule
d) 0.245 joule
Explanation:
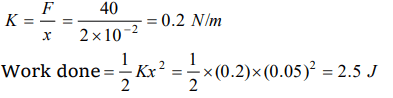
8. A wire of length L and cross-sectional area A is
made of a material of Young's modulus Y. It is
stretched by an amount x. The work done is
a) \[\frac{YxA}{2L}\]
b) \[\frac{Yx^{2}A}{L}\]
c) \[\frac{Yx^{2}A}{2L}\]
d) \[\frac{2Yx^{2}A}{L}\]
Explanation: \[\frac{Yx^{2}A}{2L}\]
9. The elastic energy stored in a wire of Young's modulus Y is
a) \[Y\times\frac{Strain^{2}}{Volume}\]
b) \[Stress\times Strain \times Volume\]
c) \[\frac{Strain^{2}\times Volume}{2Y}\]
d) \[\frac{1}{2} \times Y \times Stress\times Strain \times Volume\]
Explanation: \[\frac{Strain^{2}\times Volume}{2Y}\]
10. A wire of length 50 cm and cross sectional area of 1 sq. mm is extended by 1 mm. The required work
will be \[\left(Y=2\times10^{10}N m^{-2}\right)\]
a) \[6\times10^{-2}J\]
b) \[4\times10^{-2}J\]
c) \[2\times10^{-2}J\]
d) \[1\times10^{-2}J\]
Explanation: