PrepBharat

1. Let \[f\left(x\right)=\begin{cases}x^{3} \mid \cos\frac{\pi}{2x}\mid& x \neq 0\\+x^{4}\mid\sin\frac{\pi}{x}\mid\\0, & x= 0\end{cases}\]
then f is
a) differentiable at x = 0 and x = 1
b) differentiable at x = 0 not differentiable at x = 2
c) differentiable at x = 2 and not differentiable at x = 1
d) differentiable neither at x = 0 nor at x = 2.

View Answer

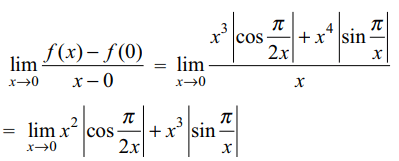
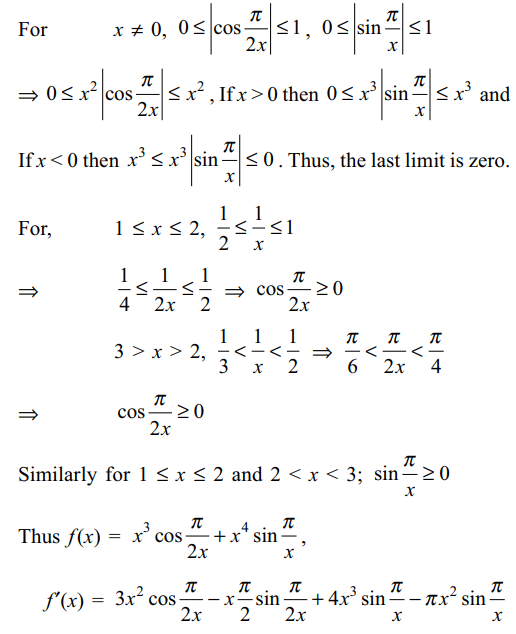
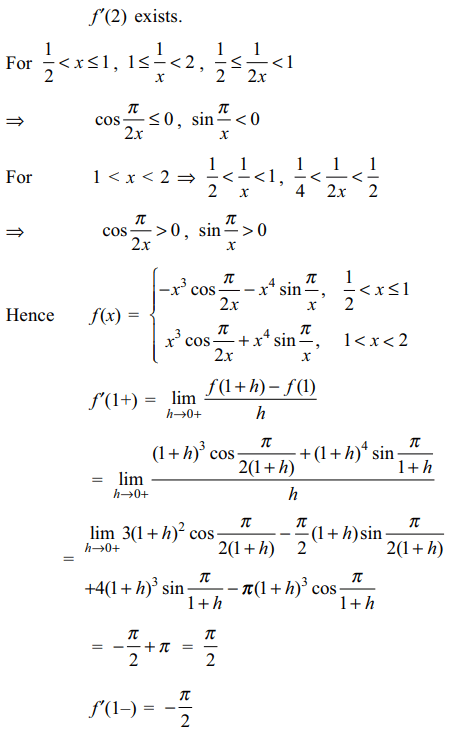
2. If \[f\left(x\right)=\cot^{-1}\left(\frac{x^{x}-x^{-x}}{2}\right)\]     then f' (1) equals
a) -1
b) 1
c) log 2
d) – log 2.

View Answer

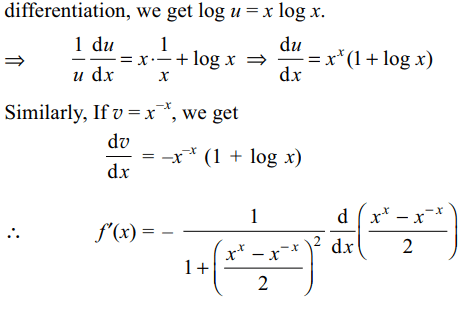
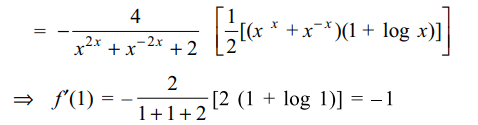
3. If \[f\left(x\right)=\left(1+x\right)^{n}\]   , then the value of \[f\left(0\right)+f'\left(0\right)+\frac{f"\left(0\right)}{2!}+....+\frac{\left(0\right)}{}\]       is
a) n
b) \[2^{n}\]
c) \[2^{n+1}\]
d) none of these

View Answer

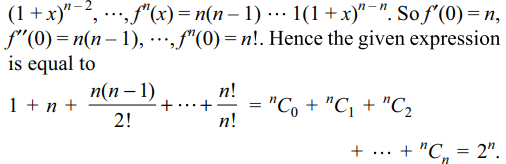
4. The solution set of f '(x) > g'(x) where \[f\left(x\right)=\left(1/2\right)5^{2x+1}\]     and \[g\left(x\right)=5^{x}+4x\log 5\]     is
a) \[\left(1,\infty\right)\]
b) \[\left(0,1\right)\]
c) \[\left[0,\infty\right)\]
d) \[\left(0,\infty\right)\]

View Answer

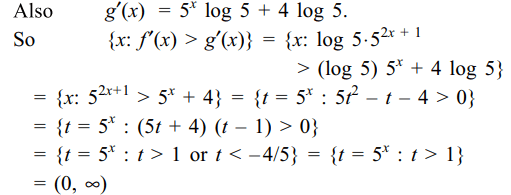
5.Let \[f\left(x\right)=\sin x;g\left(x\right)=x^{2}\]     and h(x) = log x. If u (x) = h( f (g(x))), then \[\frac{d^{2}u}{dx^{2}}\mid x=\sqrt{\pi}/2\]     is
a) \[2-\pi\]
b) \[2-2\pi\]
c) \[\pi-2\]
d) \[2\pi-2\]

View Answer

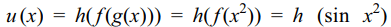
6. If \[y=\tan^{-1}\frac{1}{1+x+x^{2}}+\tan^{-1}\frac{1}{x^{2}+3x+3}+\tan^{-1}\frac{1}{x^{2}+5x+7}+....+\]
up to n terms, then y'(0) is equal to
a) \[-\frac{1}{1+n^{2}}\]
b) \[-\frac{n^{2}}{1+n^{2}}\]
c) \[\frac{n}{1+n^{2}}\]
d) none of these

View Answer

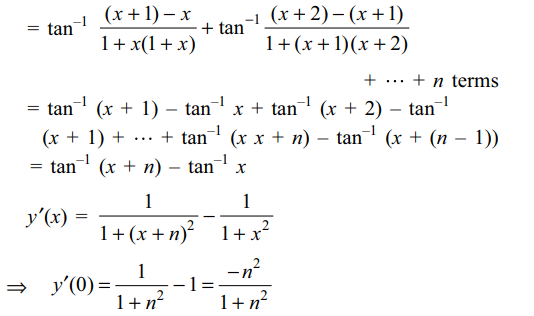
7. Let f and g be functions satisfying
\[f\left(x\right)=e^{x}g\left(x\right),f\left(x+y\right)=f\left(x\right)+f\left(y\right),g\left(0\right)=0 , g'\left(0\right)=4\]
g and g' are continuous at 0. Then
a) f (x) = 0 for all x
b) f (x) = x for all x
c) f (x) = x + 4 for all x
d) f (x) = 4 x for all x

View Answer

8. Let \[f:R\rightarrow R\]   is a function which is defined by \[f\left(x\right)=\max\left\{x,x^{3}\right\}\]    . The set of all points on which f (x) is not differentiable is
a) \[\left\{-1,1\right\}\]
b) \[\left\{-1,0\right\}\]
c) \[\left\{0,1\right\}\]
d) \[\left\{-1,0\right\}\]

View Answer

9. Which of the following functions is differentiable at x = 0?
a) cos (|x|) + |x|
b) cos (|x|) – |x|
c) sin |x| + |x|
d) sin (|x|) – |x|

View Answer

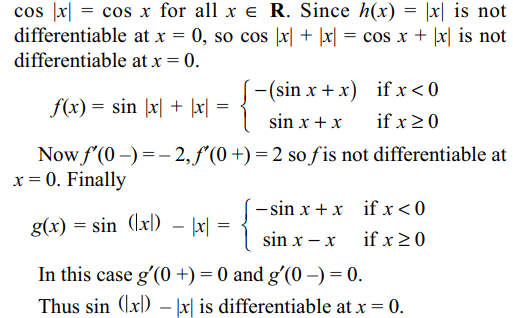
10. If f is a differentiable function at a point 'a’ and \[f'\left(a\right)\neq0\]   then which of the following is true.
a) \[-f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a\right)-f\left(a-h\right)}{h}\]
b) \[\frac{1}{2}f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a+2h\right)-f\left(a+h\right)}{2h}\]
c) \[f'\left(a\right)=\lim_{h \rightarrow 0}\frac{f\left(a+2h\right)-f\left(a\right)}{h}\]
d) \[3f'\left(a\right)=\lim_{h \rightarrow \infty}\frac{f\left(a+3h\right)-f\left(a+h\right)}{h}\]

View Answer

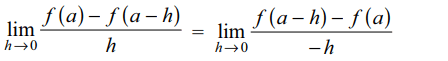
11. If f'(x) = g(x) and g'(x) = - f (x) for all x and f (2) = 4 = f' (2) then \[f^{2}\left(8\right)+g^{2}\left(8\right)\]    is
a) 16
b) 32
c) 64
d) 8

View Answer

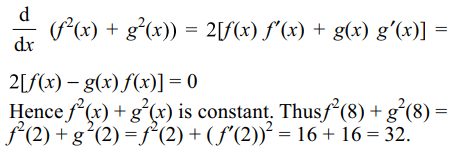
12. Let \[f\left(x\right)=\begin{cases}\sin^{2}x\left(\frac{e^{3/x}-e^{-3/x}}{e^{3/x}+e^{-3/x}}\right) & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f is not continuous at x = 0
b) f is continuous but not differentiable at x = 0
c) f is differentiable at x = 0
d) f is differentiable at x = 0 and f'(0) = 3

View Answer

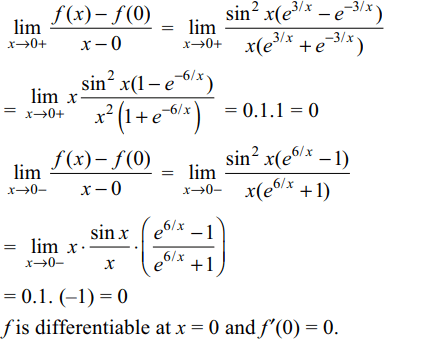
13. If \[x=2\sin t-\sin 2t,y=2\cos t-\cos2t,\]
then the value of \[\frac{d^{2}y}{dx^{2}}\]   at \[t=\pi\]  is
a) 2
b) 1/8
c) -3/4
d) -3/2

View Answer

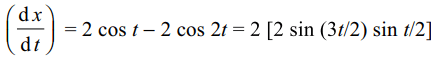
14. \[f\left(x\right)=\begin{cases}\mid x-4\mid & x \geq 1\\\left(x^{3}/2\right)-x^{2}+3x+1/2 & x < 1\end{cases}\]
then
a) f (x) is continuous at x = 1 and x = 4
b) f (x) is differentiable at x = 4
c) f (x) is continuous and differentiable at x = 1
d) f (x) is only continuous at x = 1

View Answer

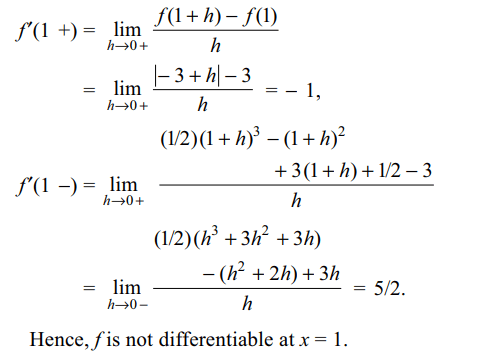
15. If \[f\left(x\right)=x^{2}+\frac{x^{2}}{\left(1+x^{2}\right)}+\frac{x^{2}}{\left(1+x^{2}\right)^{2}}+....+\frac{x^{2}}{\left(1+x^{2}\right)^{n}}+....\]
then at x =0
a) f (x) has no limit
b) f (x) is discontinuous
c) f (x) is continuous but not differentiable
d) (x) is differentiable

View Answer

16. Let \[f\left(x\right)=\begin{cases}\int_{0}^{x}\left\{1+\mid 1-t\mid\right\}dt & x > 2\\5x-7 & x \leq 2\end{cases}\]
then
a) f is not continuous at x = 2
b) f is continuous but not differentiable at x = 2
c) f is differentiable everywhere
d) f'(2+) doesn’t exist

View Answer

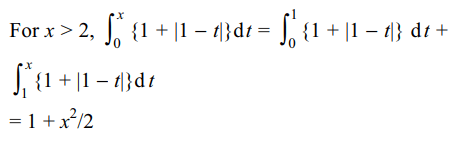
17. If \[f\left(x\right)=\mid \log_{5}\left(x^{3}+10x^{2}+11x-69\right)\mid\]
then at x = 2
a) f is not continuous
b) f is continuous but not differentiable
c) f is differentiable
d) the derivative is 1

View Answer

18. If f''(x) is continuous at x = 0 and f ''(0) = 5, then the value of \[\lim_{x \rightarrow 0}\frac{2f\left(x\right)-3f\left(2x\right)+f\left(4x\right)}{x^{2}}\]
is
a) 10
b) 8
c) 15
d) 12

View Answer

19. The solution set of f'(x) > g'(x) where \[f\left(x\right)=\left(1/2\right)5^{2x+1}\]   and \[g\left(x\right)=5^{x}+4x \log 5\]
is
a) \[\left(1,\infty\right)\]
b) \[\left(0,1\right)\]
c) \[\left[0,\infty\right)\]
d) \[\left(0,\infty\right)\]

View Answer

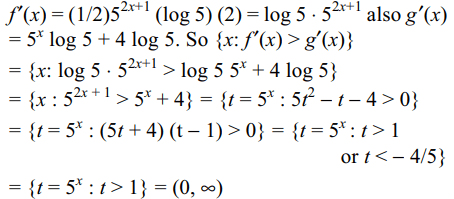
20. Suppose f is differentiable at x = 2 and \[\lim_{h \rightarrow0}\frac{f\left(2+h\right)}{h}=3\]
then
a) f '(2) = 4
b) f '(2) = 5
c) f '(2) = 6
d) f '(2) = 3

View Answer

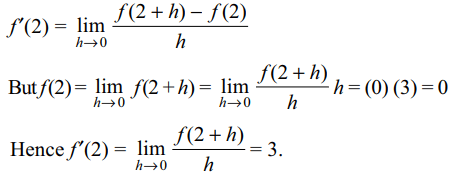
21. suppose that f is a differentiable function with the property that f (x + y) = f (x) + f (y) + xy and f '(0) = 5 then
a) f is a linear function
b) \[f\left(x\right)=3x+x^{2}\]
c) \[f\left(x\right)=5x+x^{2}/2\]
d) \[f\left(x\right)=x+\frac{5x^{2}}{2}\]

View Answer

22. If \[f\left(a\right)=a^{2},\phi\left(a\right)=b^{2}\]    and \[f'\left(a\right)=5\phi' (a)\]    then \[\lim_{x \rightarrow 0}\frac{\sqrt{f\left(x\right)}-a}{\sqrt{\phi\left(x\right)}-b}\]
is
a) \[b^{2}/a^{2}\]
b) b/a
c) 2b/a
d) 5b/a

View Answer

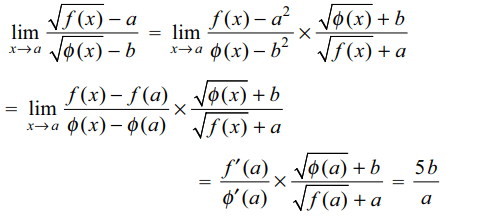
23. If \[y=\cot^{-1}\left(\frac{\sqrt{1+\sin x}+\sqrt{1-\sin x}}{\sqrt{1+\sin x}-\sqrt{1-\sin x}}\right)\]
then \[\frac{d^{2} y}{dx^{2}}\]   is equal to
a) 0
b) 1/2
c) \[\frac{1}{1+\sin x}\]
d) \[\frac{1}{\sqrt{1+\sin x}}+\frac{1}{\sqrt{1-\sin x}}\]

View Answer

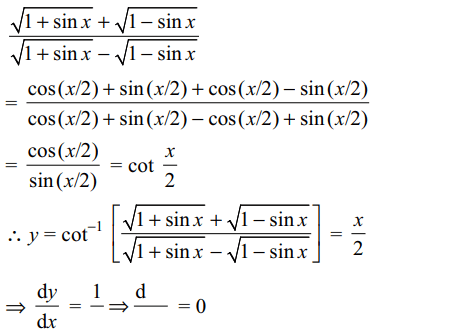
24. If \[x=\cos\theta,y=\sin^{3}\theta\]    , then \[\left(\frac{d y}{dx}\right)^{2}+y\frac{d^{2} y}{dx^{2}}\]    at \[\theta=\pi/4\]  is
a) 1
b) 2
c) -2
d) 9/4

View Answer

25. If \[y=\tan^{-1}\frac{1}{1+x+x^{2}}+\tan^{-1}\frac{1}{x^{2}+3x+3}+\tan^{-1}\frac{1}{x^{2}+5x+7}+....+\]
upto n terms, then y'' (0) is equal to
a) \[-1/\left(n^{2}+1\right)^{2}\]
b)\[-n^{2}/\left(n^{2}+1\right)^{2}\]
c) \[n^{2}/\left(n^{2}+1\right)^{2}\]
d) 0

View Answer

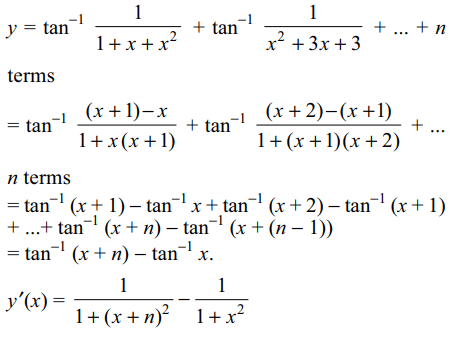
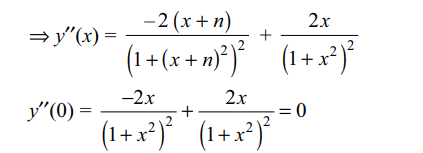
26. If \[\left(\sin x\right)\left(\cos y\right)=\frac{1}{2}\]    then \[d^{2}y/dx^{2}\]   at \[\left(\pi/4,\pi/4\right)\]   equal to
a) -4
b) -2
c) -6
d) 0

View Answer

27. If x = sin t, y = sin kt satisfies \[\left(1-x^{2}\right)y_{2}-xy_{1}+Ay=0\]
then A is equal to
a) k
b) 1
c) \[k^{2}\]
d) 1+k

View Answer

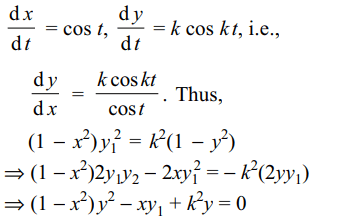
28. Let \[f\left(x\right)=\begin{cases}x^{2}/2 & if 0\leq x\leq1\\2x^{2}-3x+3/2 &if 1\leq x\leq 2\end{cases}\]
then
a) f' is not a continuous function
b) f'' is not continuous at x = 1
c) f is not differentiable at x = 1
d) f is not continuous at x = 1

View Answer

29. Let f and g be differentiable function satisf ying g'(a) = 2, g(a) = b and f o g = I (identity function). Then f '(b) is equal to
a) 1/2
b) 2
c) 2/3
d) 3/4

View Answer

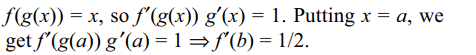
30. If \[y=x^{n}\left(a\cos\left(\log x\right)+b\sin\left(\log x\right)\right)\]       and y satisfies \[y_{2}+\left(1-2n\right)xy_{1}+Ay=0\]
then A is equal to
a) n
b) \[1+n^{2}\]
c) 1+1/n
d) \[1-n^{2}\]

View Answer

31. Let f (x) be defined by
\[f\left(x\right)=\begin{cases}\sin 2x & 0< x \leq\pi/6\\ax+b & \pi/6 < x< 1\end{cases}\]
The values of a and b such that f and f' are continuous are
a) \[a=1 , b=\frac{1}{\sqrt{2}}+\frac{\pi}{6}\]
b) \[a=\frac{1}{\sqrt{2}}=b\]
c) \[a=1 , b=\frac{\sqrt{3}}{2}-\frac{\pi}{6}\]
d) \[a=1, b=\frac{1}{2}-\frac{\pi}{6}\]

View Answer

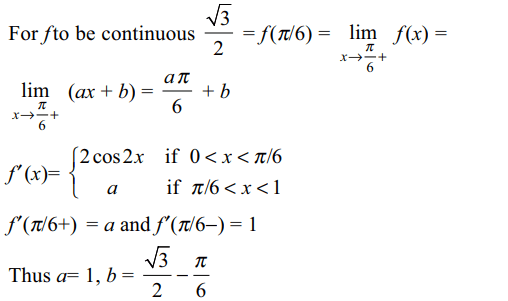
32. The coefficients a and b that make the function \[f\left(x\right)=\begin{cases}1/\mid x\mid & \mid x\mid\geq 1\\ax^{2}+b &\mid x\mid< 1\end{cases}\]
differentiable at any point are given by
a) a = - 1/2, b = 3/2
b) a = 1/2, b = - 3/2
c) a = 1, b = - 1
d) a = 1/2, b = 3/4

View Answer

33. The derivative at x = 0 of \[\tan^{-1}\frac{\sqrt{1+x^{2}}-1}{x}\]    w.r.t. \[\tan^{-1}\frac{2x\sqrt{1+x^{2}}}{1-2x^{2}}\]
is
a) 1/4
b) 1/8
c) 1/2
d) 1

View Answer

34. If \[y=\sin^{-1}\sqrt{\frac{1-x}{1+x}}\]    then y '(1/2) is equal to
a) 1
b) 1/2
c) \[-\sqrt{2}/3\]
d) \[-2\sqrt{2}/3\]

View Answer

35. If \[y=\sqrt{\frac{1-\sin^{-1}x}{1+\sin^{-1}x}}\]    then y'(0) is equal to
a) 1
b) 1/2
c) -1
d) \[\sqrt{2}/3\]

View Answer

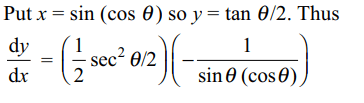
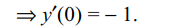
36.Let \[f\left(x\right)=e^{ax}\sin\left(bx+c\right)\]     and \[f''\left(x\right)=r^{2}e^{ax}\sin\left(bx+\theta\right)\]
then
a) \[r=a^{2}+b^{2}\]
b) \[r=\sqrt{a^{2}+b^{2}}\]
c) \[\theta=c+2\tan^{-1}\left(b/a\right)\]
d) Both b and c

View Answer

37. Let f be a function satisf ying f (x + y) = f (x) f (y) for all x and y and f (0) = f '(0) = 1 then
a) f is differentiable for all x
b) f '(x) = f (x)
c) \[f\left(x\right)=e^{x}\]
d) All of the Above

View Answer

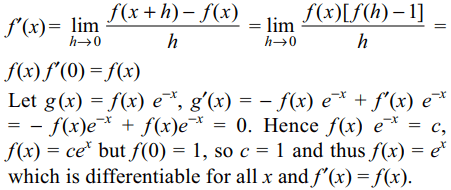
38. Let f(x) = \[x+\mid x \mid+\cos(\left[2\pi^{2}\right]x) \]     and h(x) = \[\cos\left[\pi^{2}\right]x\]    where [.] denotes the greatest integer function. Then
a) f+ g is continuous everywhere but not differentiable at x = 0
b) f+ g is differentiable at x = 0
c) fg is continuous but not differentiable at x = 0
d) Both a and c

View Answer

39. Let \[f\left(x\right)=\begin{cases}x^{2}sgn\left[x\right]+\left\{x\right\} & 0\leq x< 2\\\sin x+\mid x-3 \mid & 2\leq x< 4\end{cases}\]
wher [x] and {x} denote the greatest integer and fractional part functions. Then
a) f is discontinuous at x = 2
b) f is continuous but not differentiable at x = 1
c) f is not differentiable at x = 2
d) All of the Above

View Answer

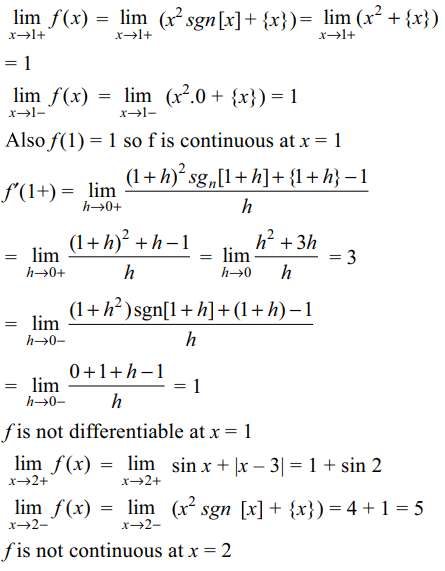
40. Let \[y=x^{8}+e^{x}\]   then
a) \[y_{10}=y_{12}\]
b) \[y_{10}=y_{11}\]
c) \[y_{11}=y_{14}\]
d) All of the Above

View Answer