PrepBharat

1. Let \[f\left(x\right)=\begin{cases}x^{2} & if x\leq x_{0}\\ax+b & if x>x_{0} \end{cases}\]
The value of the coefficients a and b for which the function is continuous and has a derivative at \[x_{0}\] , are
a) \[a=x_{0}, b=-x_{0}\]
b) \[a=2x_{0}, b=-x_0^2\]
c) \[a=x_0^2, b=-x_{0}\]
d) \[a=x_{0}, b=-x_0^2\]

View Answer

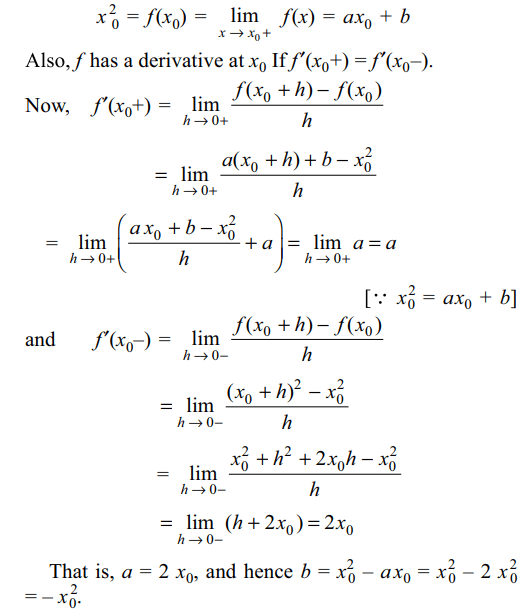
2. Given f' (2) = 6 and f' (1) = 4, \[\lim_{h \rightarrow 0}\frac{f\left(2h+2+h^{2}\right)-f\left(2\right)}{f\left(h-h^{2}+1\right)-f\left(1\right)}\]
is equal to
a) 3/2
b) 3
c) 5/2
d) -3

View Answer

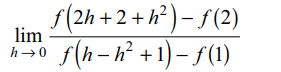
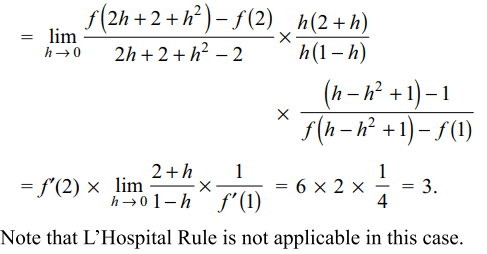
3. Let \[f:R\rightarrow R\]   be such that f (1) = 3 and f' (1) = 6. Then \[\lim_{x \rightarrow 0}\left(\frac{f\left(1+x\right)}{f\left(1\right)}\right)^{1/x}\]     equals
a) 1
b) \[e^{1/2}\]
c) \[e^{2}\]
d) \[e^{3}\]

View Answer

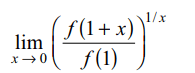
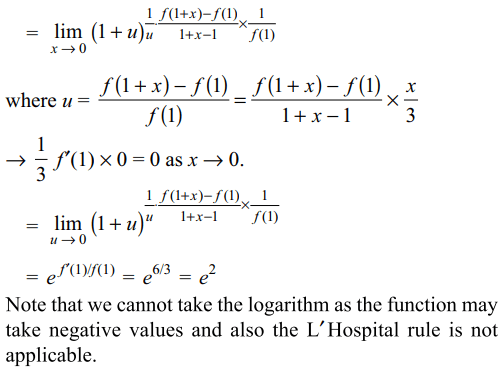
4.The domain of the derivative of the function \[f\left(x\right)=\begin{cases}\tan^{-1}x &\mid x\mid \leq1\\\frac{1}{2}\left(\mid x\mid-1\right) & \mid x\mid > 1\end{cases}\]
a) \[R \sim\left\{0\right\}\]
b) \[R \sim\left\{1\right\}\]
c) \[R \sim\left\{-1\right\}\]
d) \[R \sim\left\{-1,1\right\}\]

View Answer

5. If f (1) = 1, f' (1) = 3 then the derivative of y = f (f ( f ( f (x))) at x = 1 is
a) 256
b) 16
c) 81
d) 27

View Answer

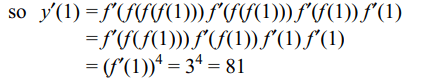
6. \[f\left(x\right)=\begin{cases}ax & x < 2\\ax^{2}-bx+3 & x \geq 2\end{cases}\]
If f is differentiable for all x then
a) a = 3/4, b = 9/4
b) a = 1, b = 2
c) a = 3/2, b = 9/2
d) a = 3/4, b = 9/2

View Answer

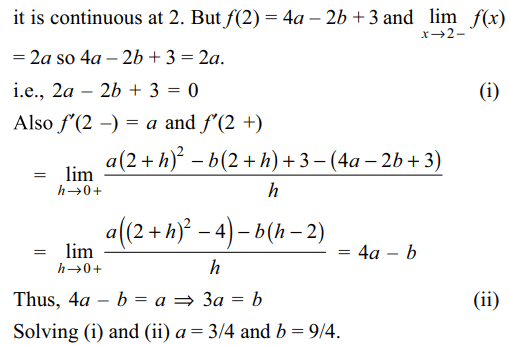
7. Let f and g be differentiable function such that f' (x) = 2g(x) and g' (x) = – f (x), and let \[T\left(x\right)=\left(f\left(x\right)\right)^{2}-\left(g\left(x\right)\right)^{2}.\]
Then T' (x) is equal to
a) T(x)
b) 0
c) 2f (x) g(x)
d) 6 f (x) g(x)

View Answer

8. Let f be a twice differentiable function such that f" (x) = – f (x) and f' (x) = g(x). If \[h'\left(x\right)=\left[f\left(x\right)\right]^{2}+\left[g\left(x\right)\right]^{2}\]      , h(1) = 7 and h(0) = 2, then h(3) is equal to
a) 11
b) 4
c) 14
d) 13

View Answer

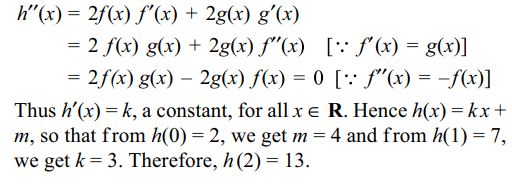
9. If \[y^{2}=P\left(x\right)\]   is a polynomial of degree 3,
\[2\frac{d}{dx}\left(y^{3}\frac{d^{2}y}{dx^{2}}\right)\]     is equal to
a) P(x) + P'(x)
b) P(x) P'(x)
c) P(x) P'''(x)
d) a constant

View Answer

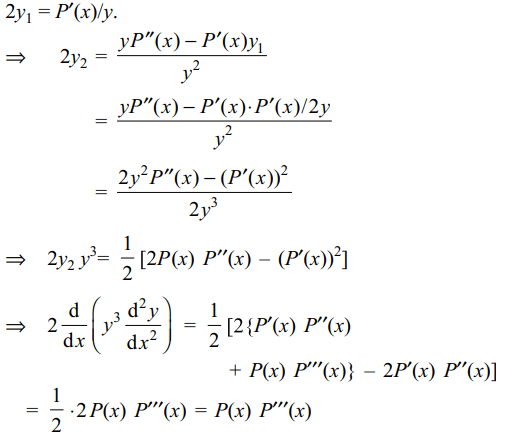
10. Let \[f\left(x\right)=\lim_{n \rightarrow \infty}\frac{\left(x^{2}+x+\frac{9}{4}+\cos\pi x\right)^{n}-1}{\left(x^{2}+x+\frac{9}{4}+\cos\pi x\right)^{n}+1}.\left(\frac{2\tan ^{n}x+x^{n}}{\tan^{n}x}\right)\]
then
a) f is differentiable for all \[x\epsilon R\]
b) f is continuous but not differentiable
c) f is discontinuous at all \[n\epsilon I\]
d) f is discontinuous only at finitely many points

View Answer

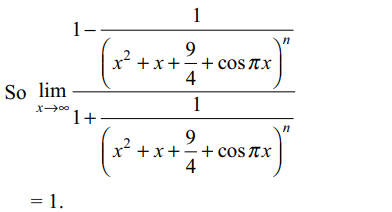
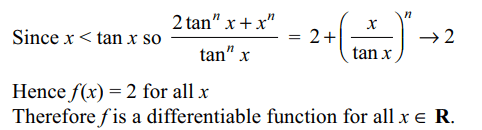
11. If \[f"\left(x\right)=\frac{\cos\left(\log x\right)}{x},f'\left(1\right)=0\]      and \[y=f\left(\frac{2x+3}{3-2x}\right)\]   , then \[\frac{dy}{dx}\mid x=1\]    is equal to
a) 4 sin (log 4))
b) 15 sin log 5
c) 12 sin (log 5)
d) 9 sin log 7

View Answer

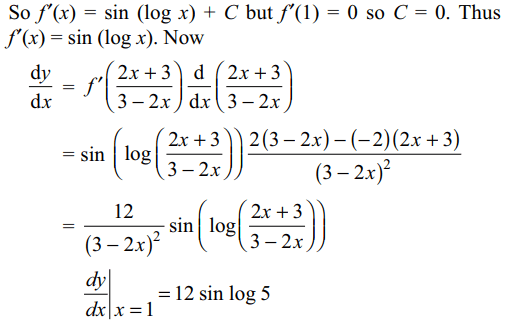
12. Which of the following could be not true If \[f"\left(x\right)=x^{-1/3}\]
a) \[f\left(x\right)=\frac{3}{2}x^{2/3}-3\]
b) \[f\left(x\right)=\frac{9}{10}x^{5/3}-7\]
c) \[f'''\left(x\right)=-\frac{1}{3}x^{-4/3}\]
d) \[f'\left(x\right)=\frac{3}{2}x^{2/3}+6\]

View Answer

13. Suppose that f(x)=[x]', the least integer function then
a) f is differentiable on [0,4]
b) there is a differentiable function on \[(- \infty, \infty)\]   whose derivative is f (x).
c) f is continuous on [0,1)
d) f is differentiable on [0,1]

View Answer

14. If \[y=e^{\sqrt{x}}+e^{-\sqrt{x}}\]     then \[xy_{2}+\left(1/2\right)y_{1}\]    is equal to
a) y
b) \[x\left(e^{\sqrt{x}}+e^{-\sqrt{x}}\right)\]
c) \[\left(1/4\right) y\]
d) \[\sqrt{x}y\]

View Answer

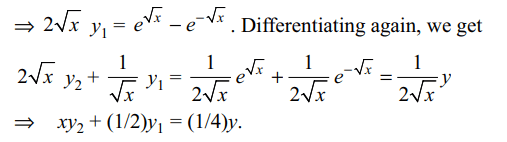
15. If \[y=\cos^{-1}\frac{x^{2n}-1}{x^{2n}+1}\]
then y'(x) is equal to
a) \[\frac{2n x^{n-1}}{x^{2n}+1}\]   If n is even
b)\[\frac{2n x^{n}}{\mid x\mid\left(x^{2n}+1\right)}\]   If n is odd
c) \[-\frac{2n x^{n}}{\mid x\mid\left(x^{2n}+1\right)}\]   If n is odd
d) \[\frac{2n x^{n-1}}{\left(x^{2n}+1\right)}\]

View Answer

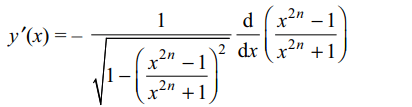
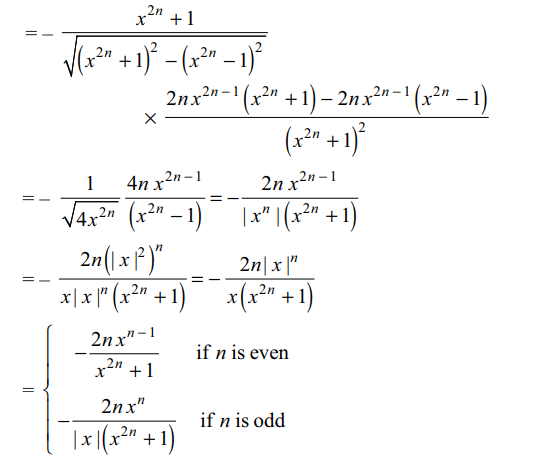
16. If \[y\left(n,x\right)=e^{x}e^{x^{2}}....e^{x^{n}},0< x < 1 \]
Then \[\lim_{n \rightarrow\infty}\frac{dy\left(n,x\right)}{dx}\]   at x = 1/2 is
a) e
b) 4e
c) 2e
d) 3e

View Answer

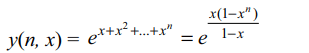
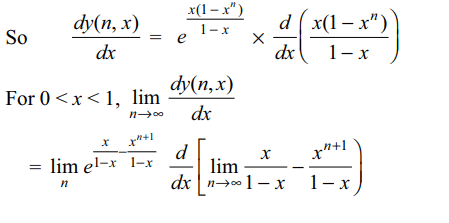
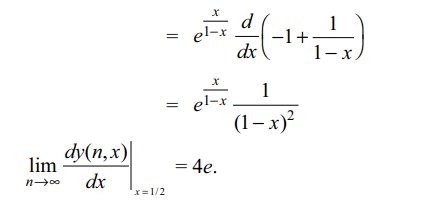
17. If \[x=a \cos t,y=a\sin t\]      then \[\frac{d^{3}y}{dx^{3}}\] at \[t=\frac{\pi}{4}\]  is
a) \[3/a^{2}\]
b) \[-12/a^{2}\]
c) \[-3/a^{2}\]
d) \[12/a^{2}\]

View Answer

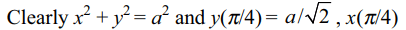
18. If \[\cos^{-1}\left(\frac{x^{2}-y^{2}}{x^{2}+y^{2}}\right)=\log a\]      then \[\frac{dy}{dx}\] is
a) y/x
b) x/y
c) \[x^{2}/y^{2}\]
d) \[y^{2}/x^{2}\]

View Answer

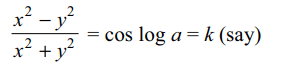
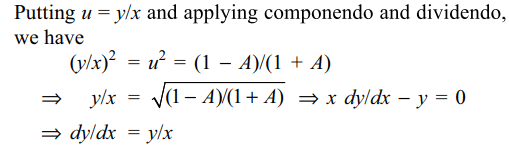
19. Let \[f\left(\frac{x+y}{2}\right)=\frac{1}{2}\left[f\left(x\right)+f\left(y\right)\right]\]      for real x and y. If f' (0) exists and equals - 1 and f (0) = 1 then the value of f (2) is
a) 1
b) -1
c) 1/2
d) 2

View Answer

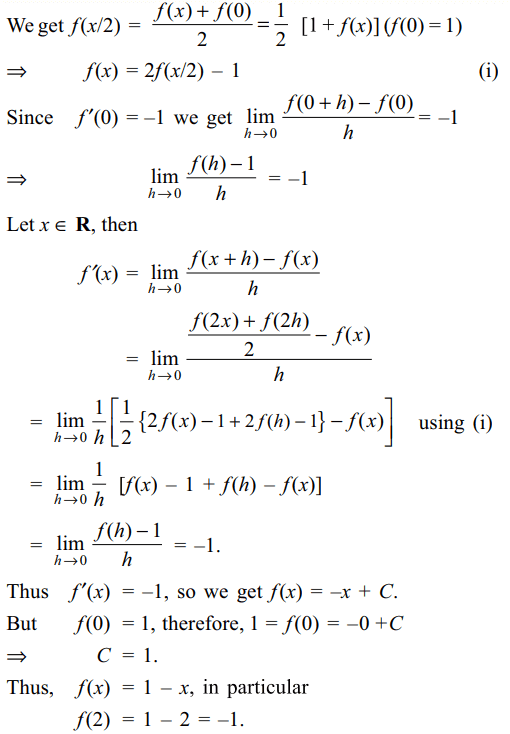
20. If \[f:R\rightarrow R\]   is a function such that \[f\left(x\right)=x^{3}+x^{2}f'\left(1\right)+xf"\left(2\right)+f'''\left(3\right)\]
for \[x\epsilon R\]  then the value of f (2) is
a) 5
b) 10
c) 6
d) -2

View Answer

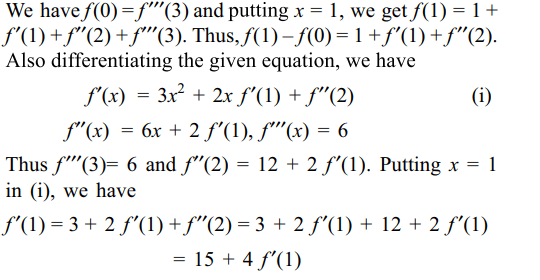
21. Let \[g\left(x\right)=\frac{(x-1)^{n}}{\log\cos^{m}\left(x-1\right)};0< x< 2\]
and m and n are integers, \[m\neq0,n>0\]  , and let p be the left hand derivative of | x – 1| at x = 1. If \[\lim_{x \rightarrow 1}g\left(x\right)=p\]    then
a) n = 1, m = 1
b) n = 1, m - 1
c) n = 2, m = 2
d) n > 1, m = n

View Answer

22. Let f be a differentiable function satisfying f (x + y) = f (x) + f (y) + xy(x + y) for all x, \[y\epsilon R\] . If f' (0) = 2, then
a) f is a polynomial function
b) f is a polynomial of degree 3 whose roots are 0, \[\pm i\sqrt{2}\]
c) f is thrice differentiable
d) All of the Above

View Answer

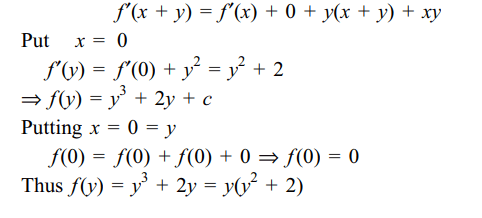
23. If \[f\left(x\right)=\begin{cases}\frac{\mid x+3\mid}{\tan^{-1}\left(x+3\right)} & x \neq-3\\4 & x = -3\end{cases}\]
then
a) f is continuous at x = –3
b) f is not derivable at x = –3
c) f is not continuous at x = –3
d) Both b and c

View Answer

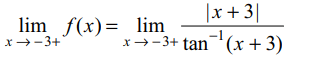
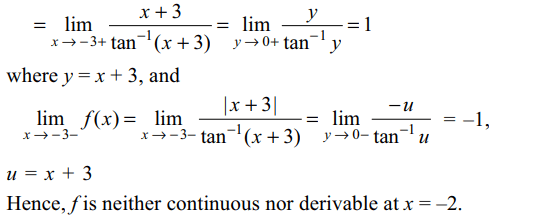
24.If x + | y | = 2y, then y as a function of x is
a) defined for all real x
b) continuous at x = 0
c) such that dy/dx = 1/3 for x < 0
d) All of the Above

View Answer

25. The function f (x) = 1 + | sin x | is
a) continuous nowhere
b) continuous everywhere
c) not differentiable at x = 0
d) Both b and c

View Answer

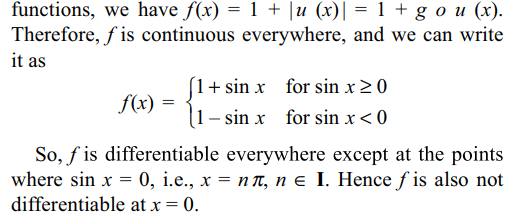
26. If \[f\left(x\right)=\sqrt{1-\sqrt{1-x^{2}}}\]     , then
a) f is continuous on [-1,1]
b) f is continuous at x = 0
c) f is not differentiable at x = 0
d) All of the Above

View Answer

27. If \[f\left(x\right)=\begin{cases}\frac{x\log\cos x}{\log\left(1+x^{2}\right)} & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f (x) is continuous at x = 0
b) f (x) is continuous at x = 0 but not differentiable at x = 0
c) f (x) is derivable at x = 0 and f ' (0) = – 1/2
d) Both a and c

View Answer

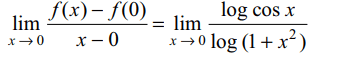
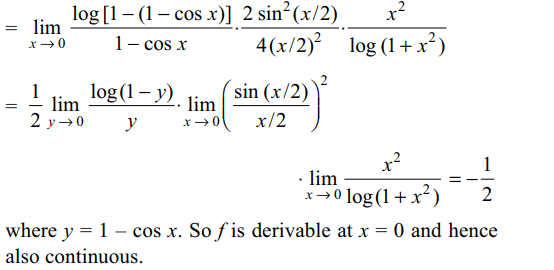
28. The function \[f\left(x\right)=\frac{x}{1+\mid x\mid}\]    is differentiable on
a) \[\left(0,\infty\right)\]
b) \[\left[0,\infty\right)\]
c) \[\left(-\infty,0\right)\]
d) All of the Above

View Answer

29. If \[f\left(x\right)=\begin{cases}x^{2}\cos\frac{1}{x} & x \neq 0\\0 & x = 0\end{cases}\]
then
a) f and f' are continuous at x = 0
b) f is derivable at x = 0
c) f is derivable at x = 0 and f' is not continuous at x=0
d) Both b and c

View Answer

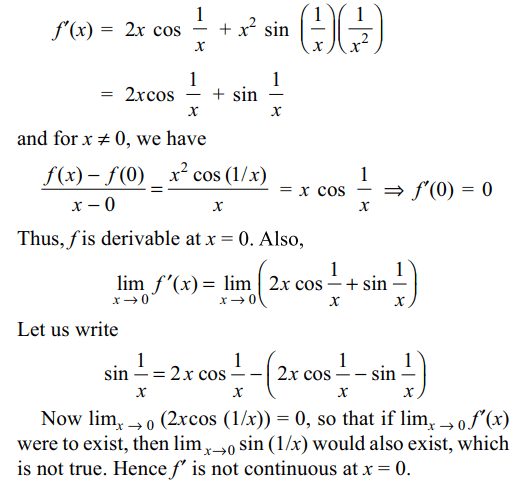
30. If \[f\left(x\right)=\sin^{-1}\frac{2x}{1+x^{2}}\]     , then
a) f is derivable for all x, with | x | < 1
b) f is not derivable at x = 1
c) f is not derivable at x = – 1
d) All of the Above

View Answer

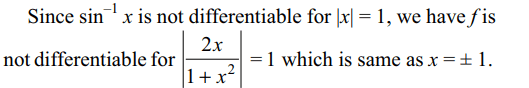
31. Let f be a differentiable function on R taking non negative values such that \[\lim_{x \rightarrow 0}\frac{f'\left(x\right)}{x}\]   exists and satisfy
\[f\left(x\right)f\left(y\right)=f\left(x_{1}\right)f\left(y_{1}\right)\]
For all \[x,y,x_{1},y_{1}\]     such that \[x^{2}+y^{2}=x_1^2+y_1^2\]    such that f (0) = 1, then
a) f is infinitely many times differentiable
b) f is an exponetial function
c) \[\lim_{x \rightarrow 0}f\left(x\right)=1\]
d) All of the Above

View Answer

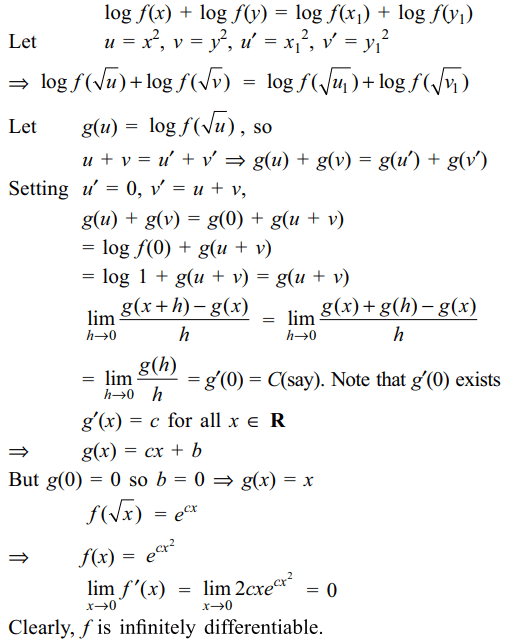
32. Let [x] denote the greatest integer less than or equal to x. If \[f\left(x\right)=\left[x\sin\pi x\right]\]    , then f (x) is
a) continuous at x = 0
b) continuous in (–1, 0)
c) differentiable in (– 1, 1)
d) All of the Above

View Answer

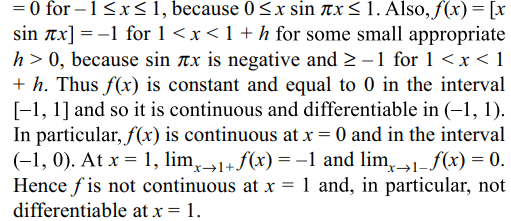
33. The function \[f\left(x\right)=\begin{cases}\mid x-3 \mid& x \geq 1\\\frac{x^{2}}{4}-\frac{3x}{2}+\frac{13}{4} & x < 1\end{cases}\]
is
a) continuous at x = 1
b) continuous at x = 3
c) differentiable at x = 1
d) All of the Above

View Answer

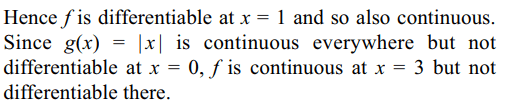
34. If \[f\left(x\right)=\begin{bmatrix}x^{n} &\sin x & -\cos x \\n! &\sin\left(n\pi/2\right)& \cos\left(n\pi/2\right)\\a &a^{2} & a^{3} \end{bmatrix}\]
the value of \[\frac{d^{n}}{dx^{n}}\left(f\left(x\right)\right)\]    at x = 0 for n = 2m + 1 is
a) independent of a
b) 0
c) \[a^{6}\]
d) Both a and b

View Answer

35. If \[f\left(x\right)=\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}\]
then
a) f is a differentiable at all points of its domain except x= 4
b) f is differentiable on \[\left(2,\infty\right)\sim\left\{4\right\}\]
c) f' (x) = 0 for all \[x\epsilon\] [2,4)
d) All of the Above

View Answer

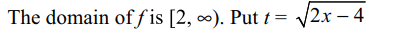
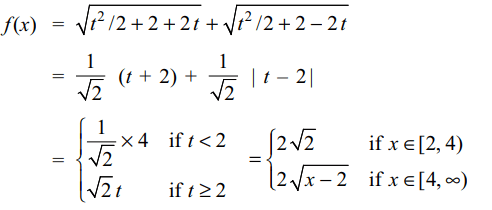
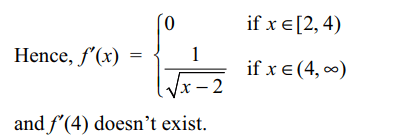
36. If f'(5) = 4 then \[\lim_{x \rightarrow \infty}\frac{f\left(5+h^{2}\right)-f\left(5-h^{2}\right)}{2h^{2}}\]
is
a) 2
b) 4
c) 3
d) 1/4

View Answer

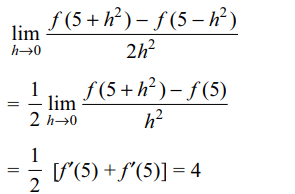
37. If \[y=\tan^{-1}\left(\frac{\log ex^{-3}}{\log ex^{3}}\right)+\tan^{-1}\left(\frac{3+3\log x}{1-9\log x}\right)\]
then \[\frac{d^{2} y}{dx^{2}}\]   is
a) 2
b) 1
c) 0
d) -1

View Answer

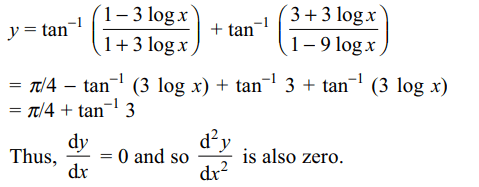
38. If \[f\left(x\right)=\frac{\tan x+\sec x -1}{\tan x-\sec x+1}\]     then \[f'\left(\pi/4\right)\]   is equal to
a) \[\sqrt{2}\left(\sqrt{2}-1\right)\]
b) \[\sqrt{2}+1\]
c) \[\sqrt{2}\left(\sqrt{2}+1\right)\]
d) \[\sqrt{2}-1\]

View Answer

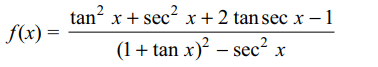
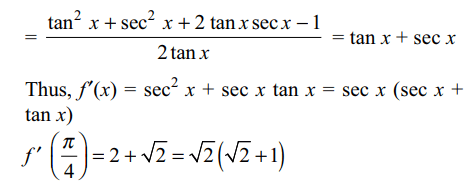
39. If \[f\left(x\right)=x^{1/x}\]    then f'' (e) is equal to
a) \[e^{1/\left({e-3}\right)}\]
b) \[e^{1/e}\]
c) \[e^{1/\left({e-2}\right)}\]
d) \[e^{1/e-3}\]

View Answer

40. If \[y=f\left(\frac{3x+4}{5x+6}\right)\]    and \[f"\left(x\right)=\tan x^{2}\]    then \[\frac{dy}{dx}\]  is equal to
a) \[-2\tan\left(\frac{3x+4}{5x+6}\right)^{2}\times\frac{1}{\left(5x+6\right)^{2}}\]
b) \[f\left(\frac{3\tan x^{2}+3}{5\tan x^{2}+6}\right) \tan x^{2}\]
c) \[ \tan x^{2}\]
d) \[ \tan \left(\frac{3x+4}{5x+6}\right)^{2}\]

View Answer