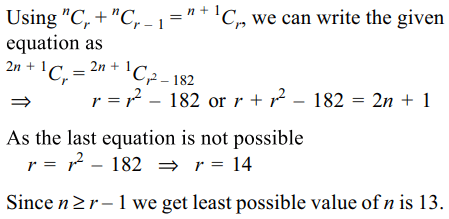1. If the cofficients of rth ,(r+1)th and (r+2)th terms in the expansion of (1 + x)n are in A.P., then n is a
root of the equation
a) \[x^{2}+x\left(4r+1\right)+4r^{2}-2=0\]
b) \[x^{2}-x\left(4r+1\right)+4r^{2}-2=0\]
c) \[x^{2}-x\left(4r+1\right)+\left(4r^{2}+2\right)=0\]
d) \[x^{2}-x\left(4r+1\right)-4r^{2}-2=0\]
Explanation:
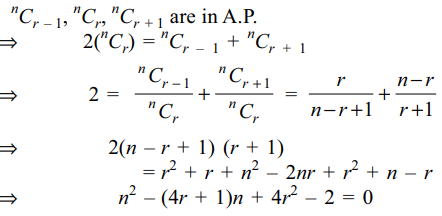
2. If \[\frac{1}{\sqrt{2x+1}}\left\{\left(1+\sqrt{2x+1}\right)^{n}-\left(1-\sqrt{2x+1}\right)^{n}\right\}= a_{0}+a_{1}x+a_{2}x^{2}+....+a_{10}x^{10}\]
then n must be equal to
a) 20, 21
b) 21, 22
c) 22, 23
d) 23, 24
Explanation:
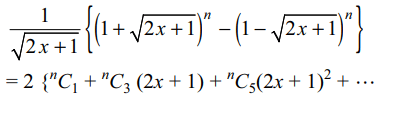
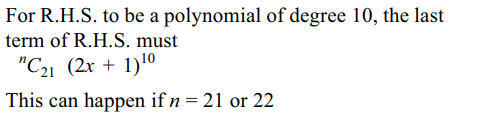
3. If in the expansion of \[\left(2^{1/3}+3^{-1/3}\right)^{n}\] , the ratio of the
7th term from the beginning to the 7th term from the
end is 1 : 6, then n
a) 6
b) 7
c) 8
d) 9
Explanation:
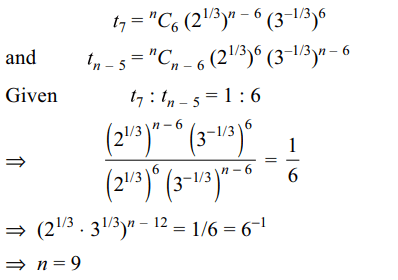
4. if sum of the coefficients of \[x^{7}\] and \[x^{4}\] in the expansion of \[\left(\frac{x^{2}}{a}-\frac{b}{x}\right)^{11}\] is zero ,then
a) ab=1
b) a=b
c) ab=-1
d) a+b=0
Explanation:
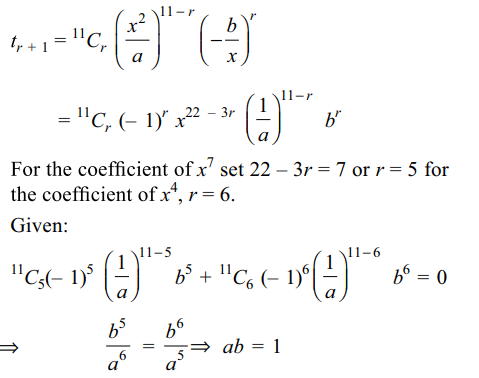
5. If n > 2 and \[\alpha,\beta,\gamma\] are three real numbers, then value
of\[S=\alpha C_{0}-\left(\alpha+\beta\right)C_{1}+\left(\alpha+2\beta+2^{n}\gamma\right)C_{2}-\left(\alpha+3\beta+3^{2}\gamma\right)C_{3}-....\] upto (n + 1) terms
is
a) 0
b) \[2^{n-2}\gamma\]
c) \[n^{2}2^{n-2}\gamma\]
d) \[n\gamma\]
Explanation:
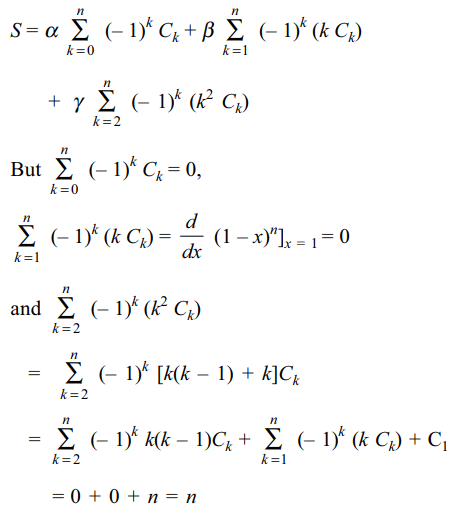
6. Value of\[\sum_{k=0}^{n}.^{n}C_{k}\sin\left(kx\right)\cos\left(n-k\right)x\] is
a) \[2^{n-1}\sin\left(nx\right)\]
b) \[2^{n}\sin\left(nx\right)\]
c) \[2^{n}\cos\left(nx\right)\]
d) none of these
Explanation:

7. If \[S_{1}=\sum_{k=0}^{n}.^{n}C_{k}\cos\left(kx\right)\cos\left(n-k\right)x\]
and
\[S_{2}=\sum_{k=1}^{n-1}.^{n}C_{k}\sin\left(kx\right)\sin\left(n-k\right)x\]
then \[S_{1}-S_{2}\]
equals
a) \[2^{n-1}\cos\left(nx\right)\]
b) \[2^{n}\cos\left(nx\right)\]
c) 0
d) \[2+2^{n}\cos nx\]
Explanation:
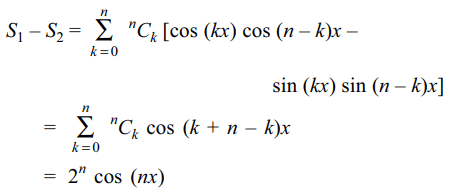
8. Sum of cofficients of all the powers of x in the expansion of
\[\left(1-2x\right)^{9}+\left(1+x\right)^{10}+\left(1-x+x^{2}\right)^{5}\]
is
a) \[2^{10}\]
b) \[2^{10}-1\]
c) \[2^{10}-2\]
d) \[2^{10}+1\]
Explanation: Put x = 1
9. Cofficients of \[x^{9}\] in the expansion of
\[\left(x^{3}+\frac{1}{2^{\log_{\sqrt{2}}{\left(x^{3/2}\right)}}}\right)^{11}\]
is
a) -5
b) 330
c) 520
d) \[5+\log_{\sqrt{2}}\]
Explanation:
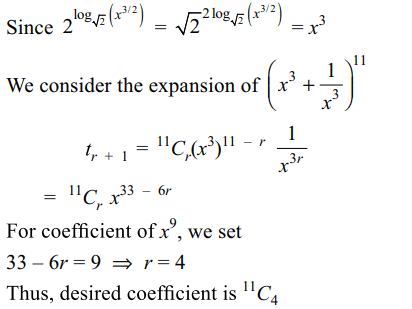
10. If n ≥ r – 1 and
\[^{n}C_{r-1}+^{n+1}C_{r-1}+^{n+2}C_{r-1}+....+^{2n}C_{r-1}=^{2n+1}C_{r^{2}-182}-^{n}C_{r}\]
then the least possible value of n is
a) 7
b) 10
c) 13
d) 14
Explanation: