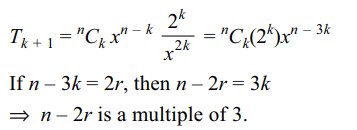1. Coeffient of \[x^{8}\] in the expansion of \[\left(1+2x-x^{3}\right)^{6}\] is
a) 528
b) -428
c) 238
d) -238
Explanation:
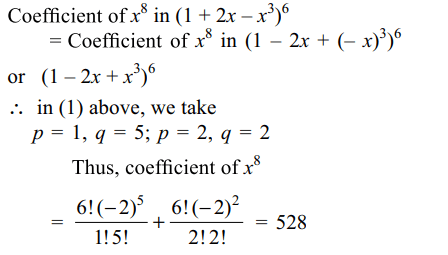
2. If the 3rd term in the expansion of
\[\left(\frac{1}{x}+x^{\log_{2}x}\right)^{5}\]
is 40 then x equals
a) \[1/\sqrt{2},2\]
b) \[\sqrt{2},4\]
c) \[1/\sqrt{2},4\]
d) \[\sqrt{2},1/\sqrt{2}\]
Explanation:
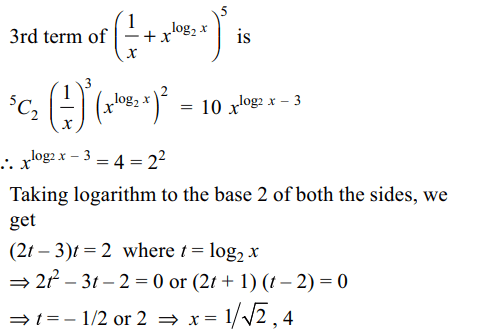
3. If the term independent of x in the expansion of
\[\left(\sqrt{x}-\frac{k}{x^{2}}\right)^{10}\] is 405, then k equals
a) 2,-2
b) 3,-3
c) 4,-4
d) 1,-1
Explanation:
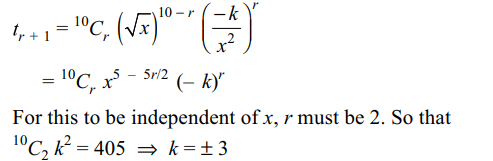
4. If the third term in the expansion \[\left(x+x^{\log_{5} x}\right)^{5}\] is 2,
then x equals
a) 1/5,5
b) \[1/5,1/\sqrt{5}\]
c) \[\sqrt{5},5\]
d) \[1/\sqrt{5},5\]
Explanation:
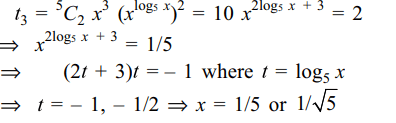
5. If the fifth term in the expansion \[\left(x^{1/3}+\frac{1}{x}\right)^{n}\] does
not depend upon x, then \[^{n}C_{2}+^{n}C_{14}\] equals
a) 240
b) 480
c) 360
d) 120
Explanation:
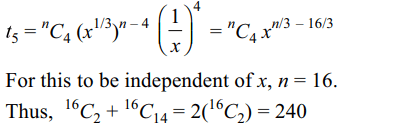
6. If the coefficients of three consecutive terms of
\[\left(1+x\right)^{n+5}\] are in the ratio 5:10:14, then n is equal to
a) 5
b) 6
c) 7
d) 8
Explanation:
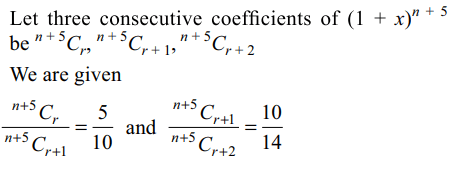
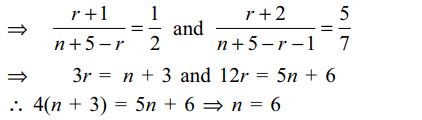
7. Cofficients of the terms independent of x in the expansion of \[\left(\frac{x+1}{x^{2/3}-x^{1/3}+1}-\frac{x-1}{x-x^{1/2}}\right)^{10}\]
is
a) 105
b) 210
c) 310
d) 180
Explanation:
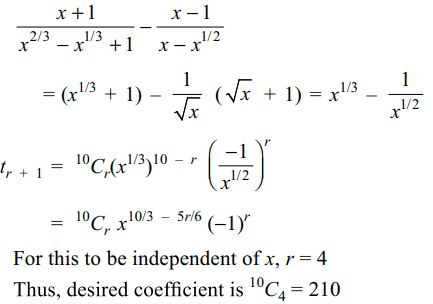
8. Value(s) of x for which the fourth term in the
expansion of \[\left(\sqrt{x}^{1/\left(\log_{2}x+1\right)}+x^{1/12}\right)^{6}\]
is 40 is (are)
a) 1/8
b) 2
c) 1/16,2
d) 1/8,4
Explanation:
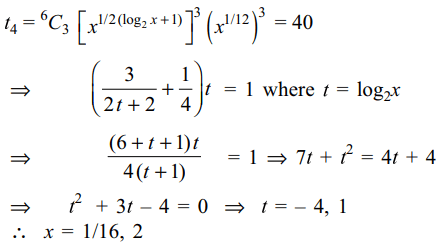
9. If \[n\epsilon N\], n ≥ 3, then value of \[S=\left(1\right)n-\frac{1}{1!}\left(n-1\right)^{2}+\frac{1}{2!}\left(n-1\right)\left(n-2\right)^{2}-\frac{1}{3!}\left(n-1\right)\left(n-2\right)\left(n-3\right)^{2}+....\]
upto n terms is
a) 1
b) \[\left(-1\right)^{n}\]
c) -1
d) 0
Explanation:
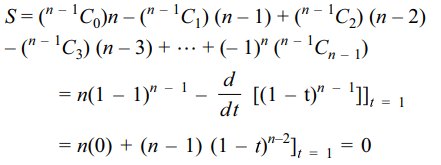
10. If \[x^{2r}\] occurs in \[\left(x+\frac{2}{x^{2}}\right)^{n}\] , then n – 2r must be of
the form
a) 3k
b) 3k-1
c) 3k+1
d) \[4k\pm1\]
Explanation: