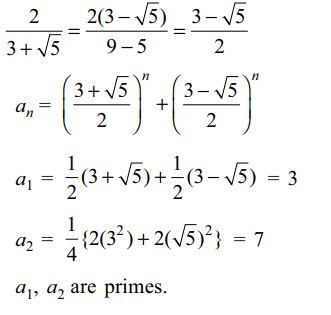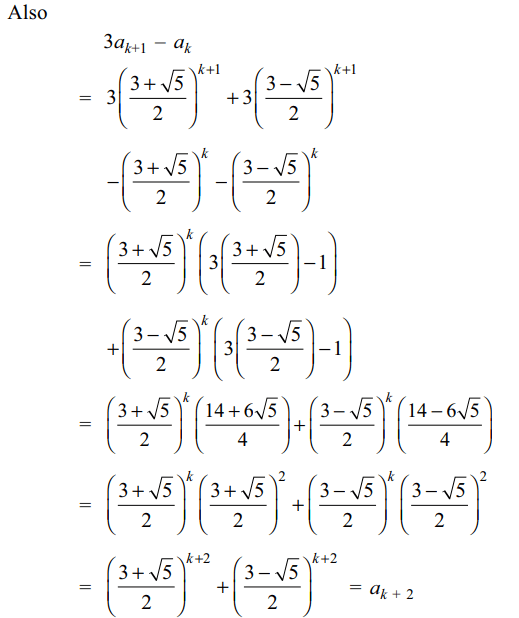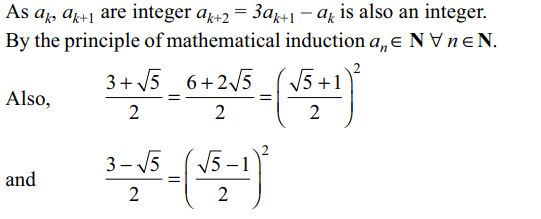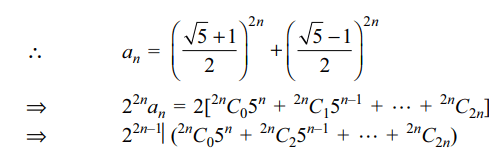PrepBharat

1. The greatest integer less than or equal to\[\left(\sqrt{2}+1\right)^{6}\]   is
a) 196
b) 197
c) 198
d) 199

View Answer

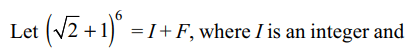
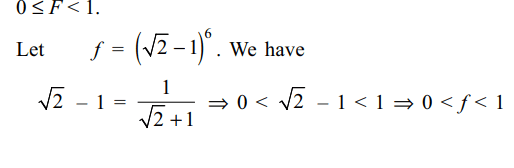
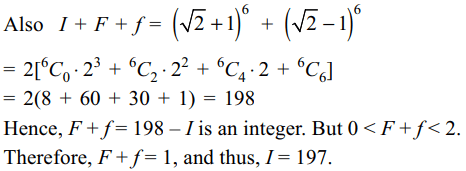
2. Sum to (n + 1) terms of the series \[\frac{C_{0}}{2}-\frac{C_{1}}{3}+\frac{C_{2}}{4}-\frac{C_{3}}{5}+....\]
is
a) \[\frac{1}{n+1}\]
b) \[\frac{1}{n+2}\]
c) \[\frac{1}{n\left(n+1\right)}\]
d) \[\frac{1}{\left(n+1\right)\left(n+2\right)}\]

View Answer

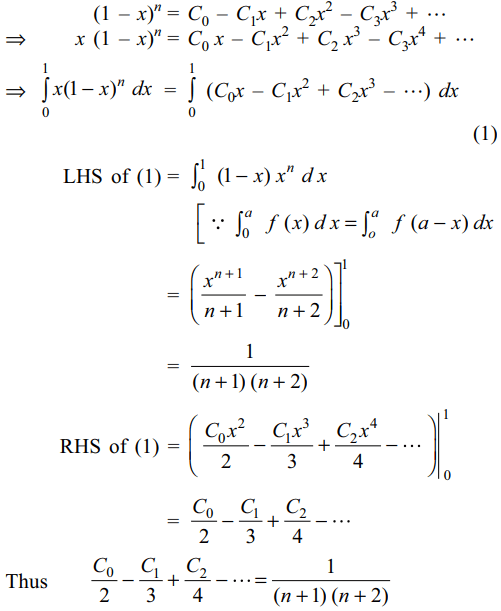
3. Value of the expression \[\frac{C_{1}}{2}+\frac{C_{3}}{4}+\frac{C_{5}}{6}+....\]     is
a) \[\frac{2^{n}-1}{n+1}\]
b) \[\frac{2^{n}}{n+2}\]
c) \[\frac{2^{n-1}}{n}\]
d) \[\frac{2^{n}}{n+1}\]

View Answer

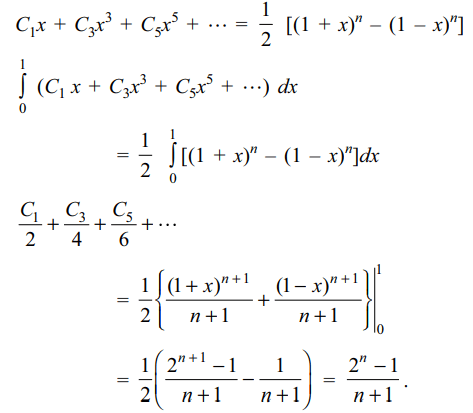
4. If \[\left(5+2\sqrt{6}\right)^{n}=m+f\]     , where n and m are positive integers and \[0\leq f< 1\]   , then \[\frac{1}{1-f}-f\]    is equal to
a) \[\frac{1}{m}\]
b) m
c) \[m+\frac{1}{m}\]
d) \[m-\frac{1}{m}\]

View Answer

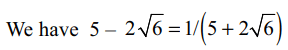
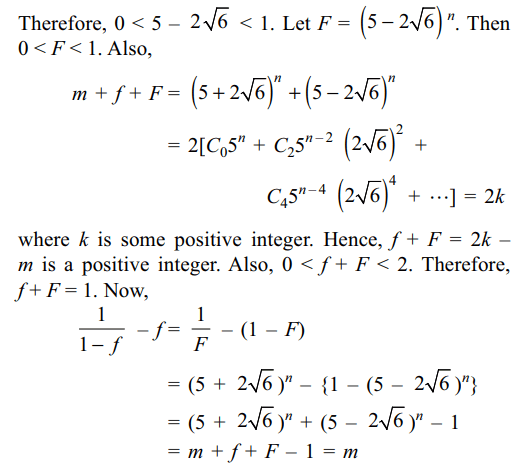
5. The number of distinct terms in the expansion of \[\left(x_{1}+x_{2}+....+x_{n}\right)^{3}\]     is
a) \[^{n+1}C_{3}\]
b) \[^{n+2}C_{3}\]
c) \[^{n+3}C_{3}\]
d) \[^{n}C_{3}\]

View Answer

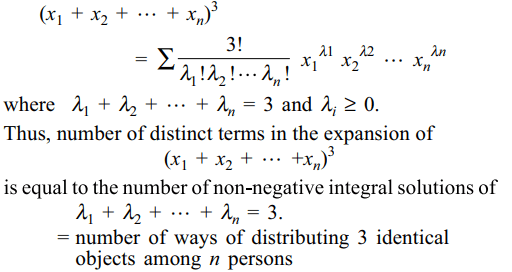
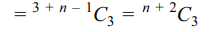
6. cofficient of \[x^{10}\] in the expansion of\[\left(1+x^{2}-x^{3}\right)^{8}\]    is
a) 476
b) 496
c) 506
d) 528

View Answer

7. The remainder when \[2^{2003}\]  is divided by 17 is
a) 2
b) 4
c) 8
d) 16

View Answer

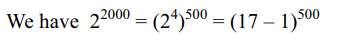
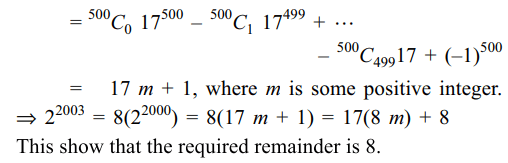
8. The interval in which x (> 0) must lie so that the greatest term in the expansion of \[\left(1+x\right)^{2n}\]    has the greatest coefficient is
a) \[\left(\frac{n-1}{n},\frac{n}{n-1}\right)\]
b) \[\left(\frac{n}{n+1},\frac{n+1}{n}\right)\]
c) \[\left(\frac{n}{n+2},\frac{n+2}{n}\right)\]
d) none of these

View Answer

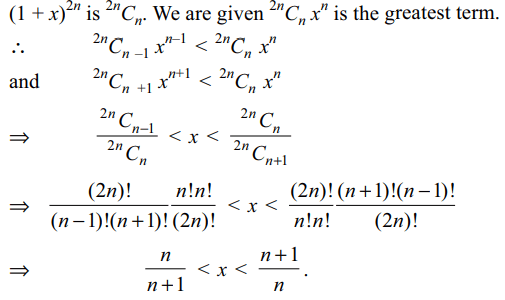
9. The largest term in the expansion of \[\left(3+2x\right)^{51}\]  , where x = 1/5, is
a) 5th
b) 6th
c) 8th
d) 9th

View Answer

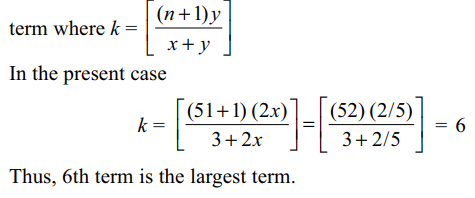
10. Let \[a_{n}=\left(\frac{3+\sqrt{5}}{2}\right)^{n}+\left(\frac{2}{3+\sqrt{5}}\right)^{n}\forall n\epsilon N\]
a) \[a_{1},a_{2}\] are primes
b) If \[a_{k},a_{k+1}\]  are integers then \[a_{k+2}\]  is an integer
c) \[a_{n}\] is an integer for each \[n\epsilon N\]
d) All of the above

View Answer