1. I. The probability of encountering 54 Sundays in a leap year
II. The probability of encountering 53 Sundays in a non-leap year
a) I > II
b) I < II
c) I = II
d) Nothing can be said
Explanation: There are 5 weeks and 2 days in a leap year.
Therefore, 53 Sundays can occur if 1st of Jan is either a Saturday or a Sunday, but 54 Sundays cannot be their in a leap year.
2. A,B,C and D are four towns any three of which are non-colinear. Then the number of ways to construct three roads each joining
a pair of towns so that the roads do not form a triangle is
a) 7
b) 8
c) 9
d) More than 9
Explanation: To construct 2 roads, three towns can be selected out of 4 in 4 ×3×2 = 24 ways.
Now if the third road goes from the third town to the first town, a triangle is formed, and if it goes to the fourth town, a triangle is not formed. So, there are 24 ways to form a triangle and 24 ways of avoiding a triangle
3. Boxes numbered 1, 2, 3, 4 and 5 are kept in a row and they are to be filled with either a red or a blue ball, such that no two adjacent
boxes can be filled with blue balls. Then how many different arrangements are possible, given that all balls of a given colour are
exactly identical in all respects?
a) 8
b) 10
c) 15
d) 22
Explanation: Each box can be filled in 2 ways. Hence, total no. of ways = 25 = 32
Blue balls cannot be filled in adjacent boxes
Total no. of such cases in which blue ball is filled in 2 adjacent boxes is 2 blue + 3 blue + 4 blue + 5 blue
= 4 ways ( 12, 23, 34, 45) + 3 ways ( 123, 234, 345) + 2 ways (1234, 2345) + 1 way
= 10 ways
Hence, total cases in which blue balls can not be filled in adjacent boxes = 32 – 10 = 22
4. A man has nine friends – four boys and five girls. In how many ways can he invite them, if there have to be exactly three girls in
the invitees?
a) 320
b) 160
c) 80
d) 200
Explanation:
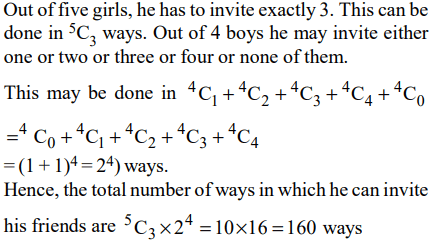
5. In how many ways can the eight directors, the vice-chairman and the chairman of a firm be seated at a round-table, if the
chairman has to sit between the vice-chairman and the director?
a) 9! × 2
b) 2 × 8!
c) 2 × 7!
d) None of these
Explanation: Let the vice-chairman and the chairman from 1 unit along with the eight directors, we now have to arrange 9 different units in a circle.
This can be done in 8! ways.
At the same time, the vice-Chairman & the chairman can be arranged in two different ways. Therefore, the total number of ways = 2 × 8!.
6. ABC is a three-digit number in which A > 0. The value of ABC is equal to the sum of the factorials of its three digits. What is the
value of B?
a) 9
b) 7
c) 4
d) 2
Explanation: Seeing the options. Since 7! = 5040 and 9! = 362880 are four and 6 digit numbers respectively, hence, B can’t be 7 or 9.
3 digits number will be of the form 100 A + 10 B + C.
100A + 10B + C = A! + B! + C!
Now by hit & trial method
i.e., with B = 2 and B = 4 find which one is better.
Hence, B = 4, A = 1 , C = 5
7. How many numbers can be formed from 1,2,3,4 and 5 (without repetition), when the digit at the units place must be greater than
that in the tenth place?
a) 54
b) 60
c) \[\frac{5!}{3}\]
d) 2 × 4!
Explanation: The numbers should be formed from 1, 2, 3, 4 and 5 (without repetition), such that the digit at the units place must be greater than in the tenth place. Tenth place has five options.
If 5 is at the tenth place then the digit at the unit’s place cannot be filled by the digit greater than that at the tenth place.
If 4 is at the tenth place, then the unit’s place has only option of 5, while the three places can be filled up in 3! Ways.
If 3 is at the tenth place, then the units’ place can be filled up by 4 or 5, i.e. in 2 ways. While other three places can filled up in 3! ways.
If 2 is at the tenth place, then the unit’s place can be filled up by 3, 4 or 5 i.e. in 3 ways. While other three places can be filled up in 3! Ways.
If 1 is at the tenth place, then any other four places can be filled up in 4! Ways.
Thus the total number of numbers satisfying the given conditions is
0 + 3! + 2(3!) + 3(3!) + 4! = 60.
8. How many five digit numbers can be formed using 2,3,8,7,5 exactly once such that the number is divisible by 125?
a) 0
b) 1
c) 4
d) 3
Explanation: Only those numbers which last 3 digits are divisible by 125 are divisible by 125.
So, those contain 375 & 875 at the end and the remaining two digits at the unit and tenth places can be arranged in two different ways.
Therefore, 4 such number can be formed
9. A, B, C, D, ..................X, Y, Z are the players who participated in a tournament. Everyone played with every other player exactly
once. A win scores 2 points, a draw scores 1 point and a loss scores 0 points. None of the matches ended in a draw. No two players
scored the same score. At the end of the tournament, the ranking list is published which is in accordance with the alphabetical
order. Then
a) M wins over N
b) N wins over M
c) M does not play with N
d) None of these
Explanation: Each one of the 26 players played 25 matches and none of the matches ended in a draw.
Hence, all the scores must be even. Also each one of them scored different from the other.
The maximum score possible is 50 and minimum score is 0.
There are exactly 26 possible scores, 50, 48, 46 .....0.
The ranking is in a alphabetical order means
A scored 50, B – 48, Z – 0.
This is possible if A wins all the matches B loses only to A win against all others etc.
In final rank, every player win only with all players who are below in final ranking . Since M > N hence M wins over N.
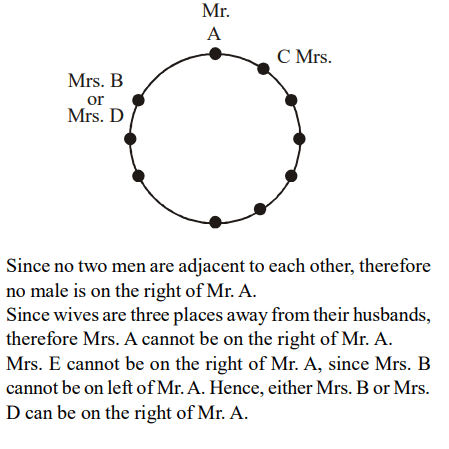
10. Five persons A, B, C, D and E along with their wives are seated around a round table such that no two men are adjacent to each
other. The wives are three places away from their husbands. Mrs. C is on the left of Mr. A, Mrs. E is two places to the right of Mrs.
B. Then, who is on the right hand side of Mr. A?
a) Mrs.B
b) Mrs.D
c) Mrs.E
d) Either Mrs B or Mrs D
Explanation: