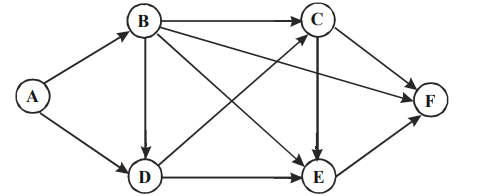
1. The figure below shows the network connecting cities A, B, C, D, E and F. The arrows indicate permissible direction of travel.
What is the number of distinct paths from A to F?
a) 9
b) 10
c) 11
d) None of these
Explanation: Paths from A to F are
ABCF, ADEF, ABEF, ADCF, ABDEF, ABDCF, ABDCEF, ABCEF, ADCEF and ABF
Hence, 10 possible distinct roots
2. Let n be the number of different 5 digit numbers, divisible by 4 with the digits 1, 2, 3, 4, 5, and 6, no digit being repeated in the
numbers. What is the value of n?
a) 144
b) 168
c) 192
d) None of these
Explanation:
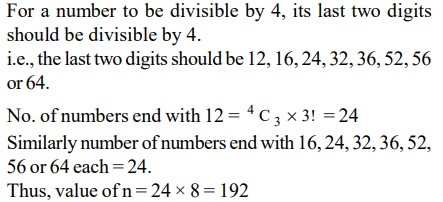
3. 10 straight lines, no two of which are parallel and no three of which pass through any common point, are drawn on a plane. The
total number of regions (including finite and infinite regions) into which the plane would be divided by the lines is
a) 56
b) 255
c) 1024
d) not unique
Explanation: For 2 such lines, no. of regions formed are 4
For 3 lines no. of regions formed are 7 (= 4 + 3)
For 4 lines, no. of regions formed are 11 (= 7 + 4)
For 5 lines no. of regions formed are 16 (= 11 + 5)
Similarly for 6, 7, 8, 9 and 10 lines, no. of regions are
16 + 6 = 22
22 + 7 = 29
29 + 8 = 37
37 + 9 = 46
46 + 10 = 56
For 10 lines no. of regions = \[^{10}C_{2}\] + 10 + 1 = 45 + 11 = 56
4. In how many ways is it possible to choose a white square and a black square on a chess board so that the squares must not lie
in the same row or column?
a) 56
b) 896
c) 60
d) 768
Explanation:

5. How many numbers greater than 0 and less than a million can be formed with the digits of 0, 7 and 8?
a) 486
b) 1086
c) 728
d) None of these
Explanation: No. of 1 digit numbers = 2
No. of 2 digit numbers = 3 × 2 = 6
No. of 3 digit numbers = 3 × 3 × 2 = 18
No. of 4 digit numbers = 33 × 2 = 54
No. of 5 digit numbers = 34 × 2 = 162
No. of 6 digit numbers (less than a million) = 35 × 2 = 486
Required numbers = 486 + 162 + 54 + 18 + 6 + 2 = 728
6. If there are 10 positive real numbers \[n_{1}< n_{2}< n_{3}......< n_{10}\] .
How many triplets of these numbers \[\left(n_{1}, n_{2}, n_{3}\right)\left(n_{2}, n_{3}, n_{4}\right).....\] can be
generated such that in each triplet the first number is always less than the second number, and the second number is always less
than the third number?
a) 45
b) 90
c) 120
d) 180
Explanation:

7. Let S be the set of five-digit numbers formed by the digits 1, 2, 3, 4 and 5, using each digit exactly once such that exactly two odd
positions are occupied by odd digits. What is the sum of the digits in the rightmost position of the numbers in S?
a) 228
b) 216
c) 294
d) 192
Explanation:
There can be 2 possibilities – last digit is odd or even.
Case I : Last digit is odd. Fixing one out of 1, 3 & 5 in the last position. Then only one odd number can occupy odd position which can be chosen in \[^{2}C_{1}\] ways = 2.
One of the two odd digits can be selected for this position in again, \[^{2}C_{1}\] ways = 2.
The other odd number can be put in either of the two even places in 2 ways.
Finally the two even numbers can be arranged in 2! ways.
Hence sum of last digit of these nos. = (2 × 2 × 2 × 2)
(1 + 3 + 5) = 144 ways
Case II : Last digit is even. Then 2 odd nos. out of 3
can be arranged in \[^{3}P_{2}\]
= 3! ways.
Again the even nos. can be arranged in 2! ways
Sum = (3! × 2) (2 + 4) = 72 ways.
Total ways = 144 + 72 = 216.
8. Twenty-seven persons attend a party. Which one of the following statements can never be true?
a) There is a person in the party who is acquainted with all the twenty-six others
b) Each person in the party has a different number of acquaintances
c) There is a person in the party who has an odd number of acquaintances
d) In the party, there is no set of three mutual acquaintances
Explanation: It can be clearly established that the choices (a) , (c) and (d) may or may not be true. Statement (b) can never be true because every person cannot have a different number of acquaintances.
9. How many three digit positive integers, with digits x, y and z in the hundred’s, ten’s and unit’s place respectively, exist such that
x < y, z < y and \[x\neq 0\] ?
a) 245
b) 285
c) 240
d) 320
Explanation:
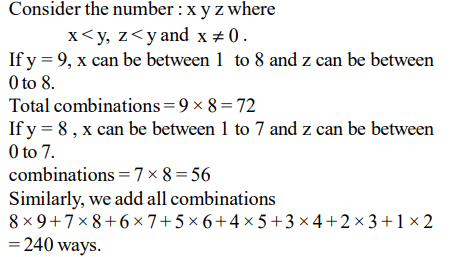
10. There are 6 boxes numbered 1,2,.........6. Each box is to be filled up either with a red or a green ball in such a way that at least 1 box
contains a green ball and the boxes containing green balls are consecutively numbered. The total number of ways in which this
can be done is
a) 5
b) 21
c) 33
d) 60
Explanation: As the boxes containing the green balls are consecutively numbered total number of ways will be
6 + 5 + 4 + 3 + 2 + 1 = 21 ways