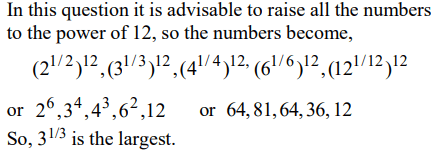1. Let a, b, c, d and e be integers such that a = 6b = 12c, and 2b = 9d = 12e. Then which of the following pairs contains a number
that is not an integer?
a) \[\left(\frac{a}{27},\frac{b}{e}\right)\]
b) \[\left(\frac{a}{36},\frac{c}{e}\right)\]
c) \[\left(\frac{a}{12},\frac{bd}{18}\right)\]
d) \[\left(\frac{a}{6},\frac{c}{d}\right)\]
Explanation:
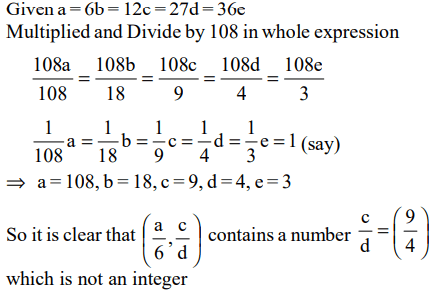
2. If a, a + 2 and a + 4 are prime numbers, then the number of possible solutions for a is
a) one
b) two
c) three
d) more than three
Explanation: a, a + 2, a + 4 are prime numbers.
Put value of ‘a’ starting from 3, we will have 3, 5 and 7 as the only set of prime numbers satisfying the given relationships
3. The remainder, when \[\left(15^{23}+23^{23}\right)\] is divided by 19, is
a) 4
b) 15
c) 0
d) 14
Explanation: The expression becomes (19 – 4)23 + (19 + 4)23
All the terms except the last one contains 19 and the last terms get cancelled out. Hence the remainder obtained on dividing by 19 will be 0
4. If \[x=\left(16^{3}+17^{3}+18^{3}+19^{3}\right)\] , then x divided by 70 leaves a remainder of
a) 0
b) 1
c) 69
d) 35
Explanation:
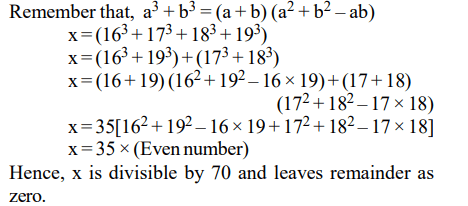
5. The digits of a three-digit number A are written in the reverse order to form another three-digit number B. If B > A and B–A is
perfectly divisible by 7, then which of the following is necessarily true?
a) 100 < A < 299
b) 106 < A < 305
c) 112 < A < 311
d) 118 < A < 317
Explanation: Let the 3 digits of number A be x, y and z
Hence A = 100x + 10y + z
On reversing the digits of number A, we get the number
B i.e., z y x.
B = 100z + 10y + x
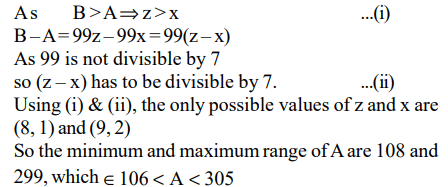
6. The rightmost non-zero digit of the number \[30^{2720}\] is
a) 1
b) 3
c) 7
d) 9
Explanation:

7. If \[\frac{30^{65}-29^{65}}{30^{64}+29^{64}}\] then
a) \[0< R\leq 0.1\]
b) \[0.1< R\leq 0.5\]
c) \[0.5< R\leq 1.0\]
d) R > 1.0
Explanation:
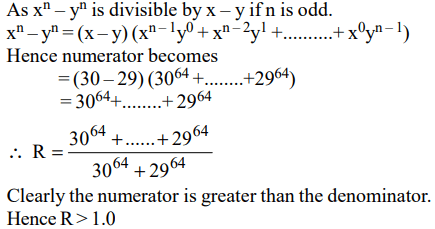
8. For a positive integer n, let \[p_{n}\] denote the product of the digits of n, and \[s_{n}\] denote the sum of the digits of n. The number of
integers between 10 and 1000 for which \[p_{n}+s_{n}=n\] is
a) 81
b) 16
c) 18
d) 9
Explanation:

9. If x = –0.5, then which of the following has the smallest value?
a) \[2^{\frac{1}{x}}\]
b) \[\frac{1}{x}\]
c) \[\frac{1}{x^{2}}\]
d) \[2^{x}\]
Explanation:
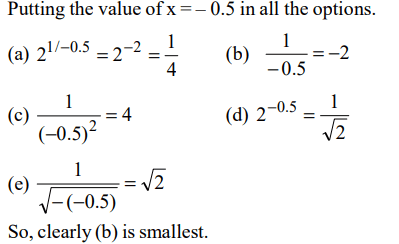
10. Which one among \[2^{1/2},3^{1/3},4^{1/4},6^{1/6}\] and \[12^{1/12}\] is the largest?
a) \[2^{1/2}\]
b) \[3^{1/3}\]
c) \[4^{1/4}\]
d) \[6^{1/6}\]
Explanation: