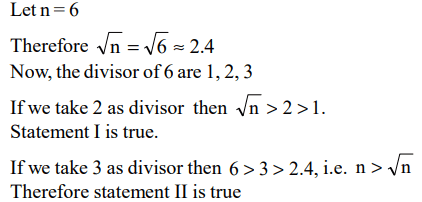1. After the division of a number successively by 3, 4 and 7, the remainders obtained are 2, 1 and 4 respectively. What will be the
remainder if 84 divides the same number?
a) 80
b) 76
c) 41
d) 53
Explanation: According to the question the required no. is
3[4 (7x + 4) + 1] + 2 = 84x + 53
So the remainder is 53, when the same number is divided by 84.
2. If u, v, w and m are natural numbers such that \[u^{m}+v^{m}=w^{m}\] , then one of the following is true
a) \[m \geq min\left(u, v,w\right)\]
b) \[m \geq max\left(u, v,w\right)\]
c) \[m < min\left(u, v,w\right)\]
d) None of these
Explanation:
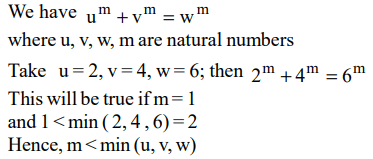
3. \[7^{6n}-6^{6n}\] , where n is an integer > 0, is divisible by
a) 13
b) 127
c) 559
d) All of these
Explanation:
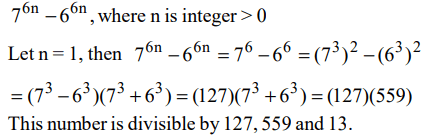
4. A positive whole number M less than 100 is represented in base 2 notation, base 3 notation, and base 5 notation. It is found that
in all three cases the last digit is 1, while in exactly two out of the three cases the leading digit is 1. Then M equals
a) 31
b) 63
c) 75
d) 91
Explanation:
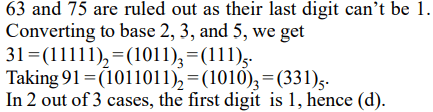
5. How many even integers n, where \[100 \leq n\leq 200\] , are divisible neither by seven nor by nine?
a) 40
b) 37
c) 39
d) 38
Explanation:

6.The number of positive integers n in the range \[12 \leq n\leq 40\] such that the product (n - 1)(n - 2)....3.2.1 is not divisible by n is
a) 5
b) 7
c) 13
d) 14
Explanation: Consider the prime numbers between 12 and 40, which are 13, 17, 19, 23, 29, 31 and 37.
Given product is not divisible by these 7 prime numbers
7.What is the remainder when \[4^{96}\] is divided by 6?
a) 0
b) 2
c) 3
d) 4
Explanation:
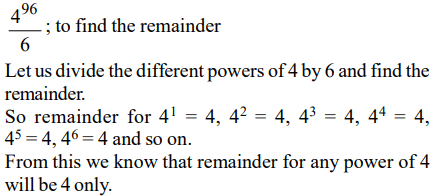
8. What is the sum of all two-digit numbers that give a remainder of 3 when they are divided by 7?
a) 666
b) 676
c) 683
d) 777
Explanation:
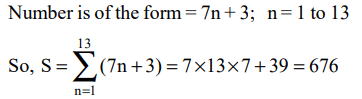
9. Let x and y be positive integers such that x is prime and y is composite. Then
a) y – x cannot be an even integer
b) xy cannot be an even integer
c) (x + y)/x cannot be an even integer
d) None of the above statements is true
Explanation:

10. Let n( > 1) be a composite integer such that \[\sqrt{n}\] is not an integer. Consider the following statements
I : n has a perfect integer-valued divisor which is greater than 1 and less than \[\sqrt{n}\] .
II : n has a perfect integer-valued divisor which is greater than \[\sqrt{n}\] but less than n
Then,
a) Both I and II are false
b) I is true but II is false
c) I is false but II is true
d) Both I and II are true
Explanation: