1. In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and \[\angle A=60^{0}\] , then the length of AD is
a) \[2\sqrt{3}\]
b) \[\frac{12\sqrt{3}}{7}\]
c) \[15\sqrt{\frac{3}{8}}\]
d) \[6\sqrt{\frac{3}{7}}\]
Explanation:
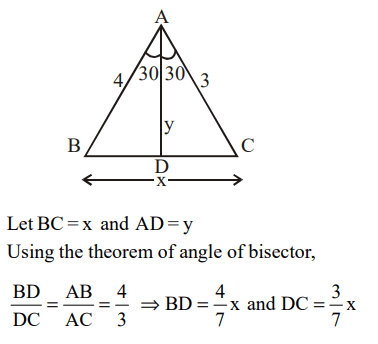
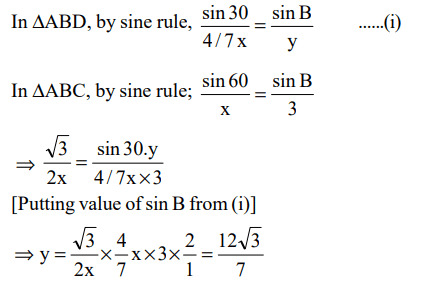
2.The length of the common chord of two circles of radii 15 cm and 20 cm, whose centres are 25 cm apart, is (in cm)
a) 24
b) 25
c) 15
d) 20
Explanation:
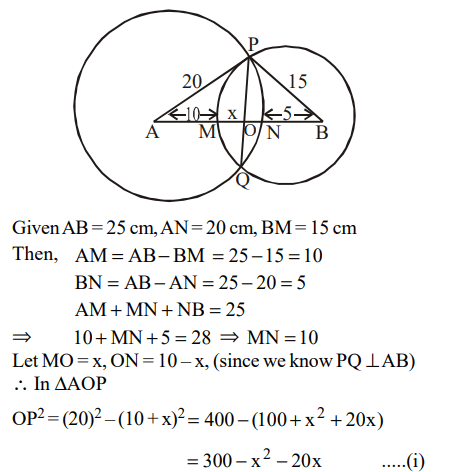
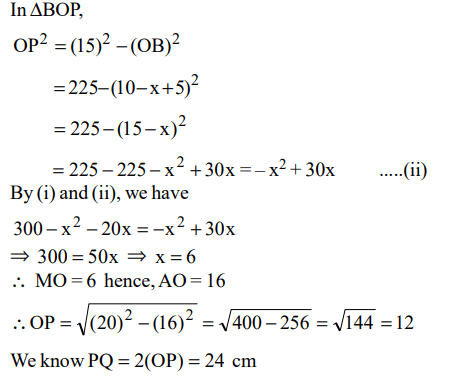
3. In the figure, ACB is a right angled triangle. CD is the altitude. Circles are inscribed within the triangles ACD, BAD. P and Q are
the centres of the circles. The distance PQ is
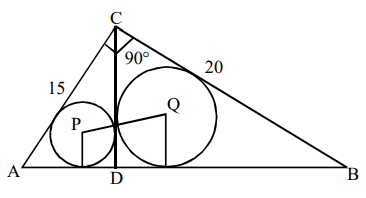
a) 5
b) \[\sqrt{50}\]
c) 7
d) 8
Explanation:
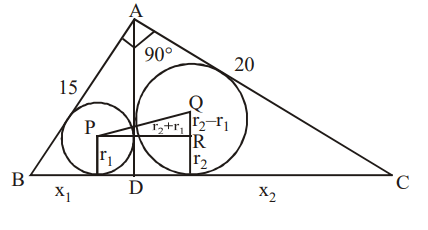
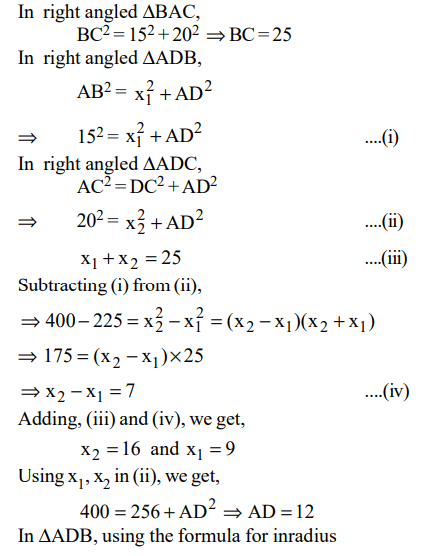
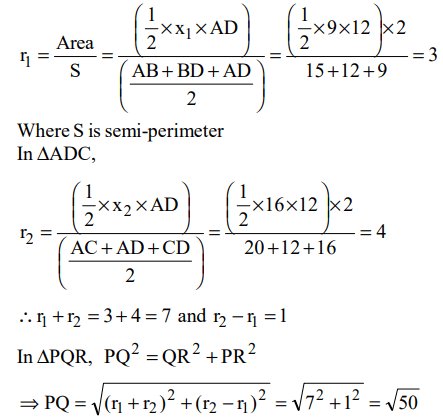
4. Instead of walking along two adjacent sides of a rectangular field, a boy took a short cut along the diagonal and saved a distance
equal to half the longer side. Then the ratio of the shorter side to the longer side is
a) 1/2
b) 2/3
c) 1/4
d) 3/4
Explanation:
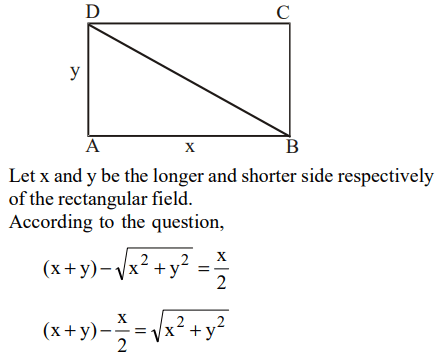
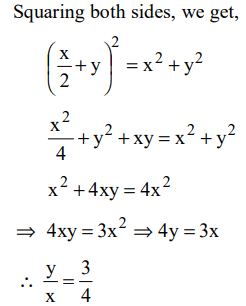
5. Each side of a given polygon is parallel to either the X or the Y axis. A corner of such a polygon is said to be convex if the internal
angle is 90° or concave if the internal angle is 270°. If the number of convex corners in such a polygon is 25, the number of
concave corners must be
a) 20
b) 0
c) 21
d) 22
Explanation: The number of convex corners is always less than concave corners by 4. Hence 25 – 4 = 21
6. In a triangle ABC, AB =6, BC = 8 and AC = 10. A perpendicular dropped from B, meets the side AC at D. A circle of radius BD (with
centre B) is drawn. If the circle cuts AB and BC at P and Q respectively, then AP: QC is equal to
a) 1 : 1
b) 3 : 2
c) 4 : 1
d) 3 : 8
Explanation:
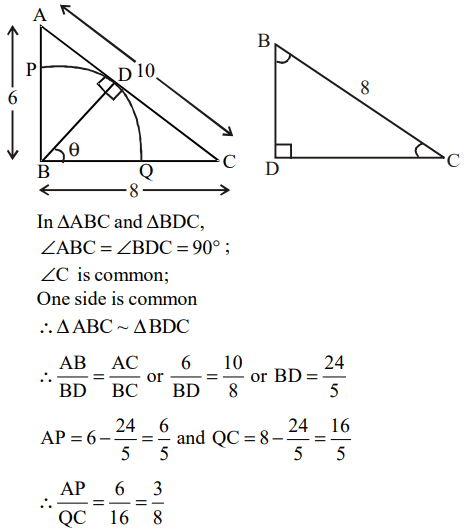
7. In the diagram given below, \[\angle ABD=\angle CDB =\angle PQD =90^{0}\] . If AB:CD = 3:1, the ratio of CD:PQ is
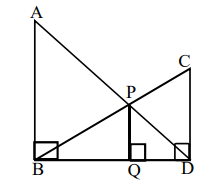
a) 1 : 0.69
b) 1 : 0.75
c) 1 : 0.72
d) None of the above
Explanation:
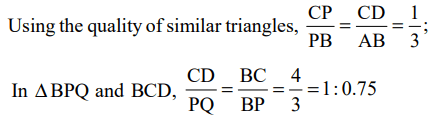
8.In the figure below, the rectangle at the corner measures 10 cm × 20 cm. The corner A of the rectangle is also a point on the
circumference of the circle . What is the radius of the circle in cm ?
a) 10 cm
b) 40 cm
c) 50 cm
d) None of these
Explanation:
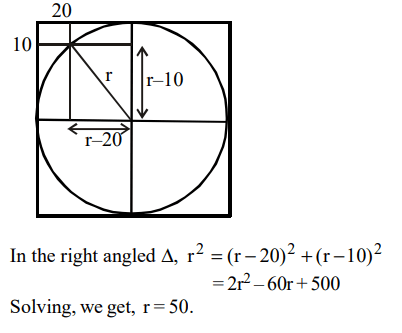
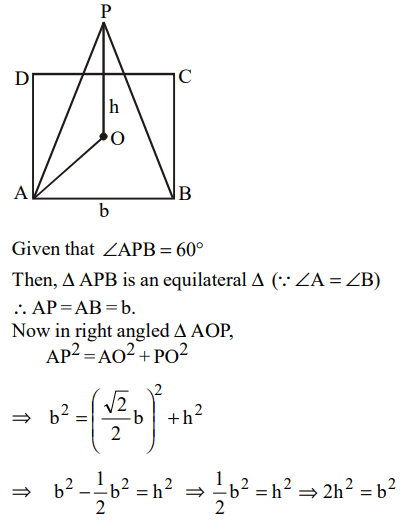
9. A vertical tower OP stands at the centre O of a square ABCD. Let h and b denote the length of OP and AB respectively. Suppose
\[\angle APB =60^{0}\] then the relationship between h and b can be expressed as
a) \[2b^{2}=h^{2}\]
b) \[2h^{2}=b^{2}\]
c) \[3b^{2}=2h^{2}\]
d) \[3h^{2}=2b^{2}\]
Explanation:
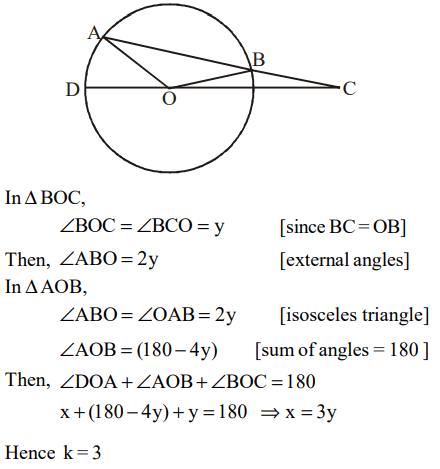
10. In the figure given below, AB is the chord of a circle with centre O. AB is extended to C such that BC=OB. The straight line CO
is produced to meet the circle at D. If \[\angle ACD=y\] degrees and \[\angle AOD=x\] degrees such that x=ky, then the value of k is
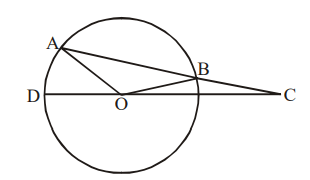
a) 3
b) 2
c) 1
d) None of these
Explanation: