1. Three circles, each of radius 20 and centres at P, Q, R. further, AB = 5, CD = 10 and EF = 12. What is the perimeter of the triangle
PQR?
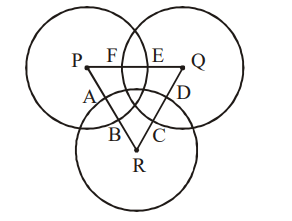
a) 120
b) 66
c) 93
d) 87
Explanation:
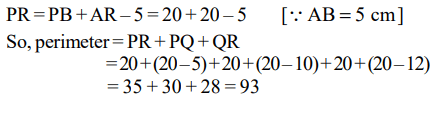
2. There is a circle of radius 1 cm. Each member of a sequence of regular polygons \[S_{1}\left(n\right),n=4,5,6....\] where n is the number of sides
of the polygon, is circumscribing the circle; and each member of the sequece of regular polygons \[S_{2}\left(n\right),n=4,5,6....\] where n is
the number of sides of the polygon, is inscribed in the circle. Let \[L_{1}\left(n\right)\] and \[L_{2}\left(n\right)\] denote the perimeters of the corresponding
polygons of \[S_{1}\left(n\right)\] and \[S_{2}\left(n\right)\] . Then
\[\frac{\left\{L_{1}\left(13\right)+2\pi\right\}}{L_{2}\left(17\right)}\]
is
a) Greater than \[\pi/4\] and less than 1
b) Greater than 1 and less than 2
c) Greater than 2
d) Less than \[\pi/4\]
Explanation:

3. The figure below shows two concentric circles with centre O. PQRS is a square inscribed in the outer circle. It also circumscribes
the inner circle, touching it at point B, C, D and A. What is the ratio of the perimeter of the outer circle to that of polygon ABCD?
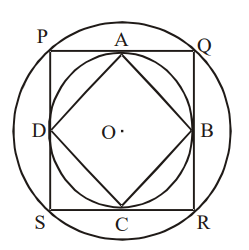
a) \[\frac{\pi}{3}\]
b) \[\pi\]
c) \[\frac{\pi}{2}\]
d) \[\frac{\pi}{4}\]
Explanation:
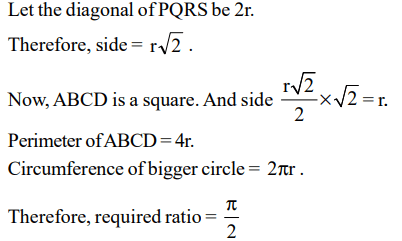
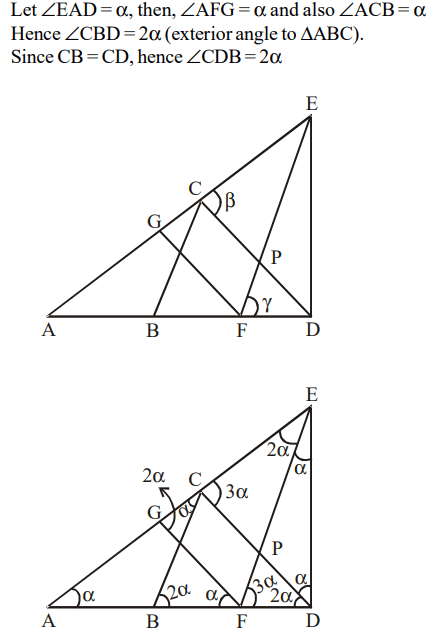
4. In the figure below, AB = BC = CD = DE = EF = FG = GA. Then, \[\angle DAE\] is approximately
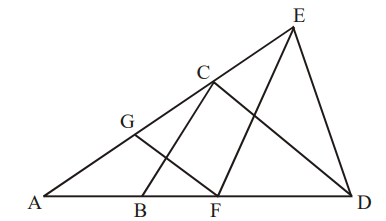
a) 15°
b) 30°
c) 20°
d) 25°
Explanation:
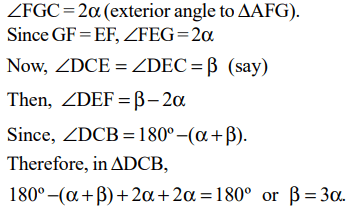
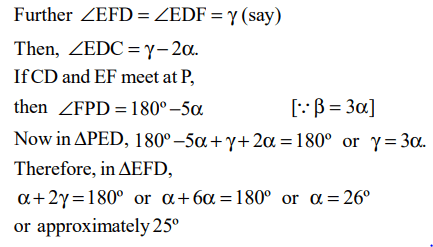
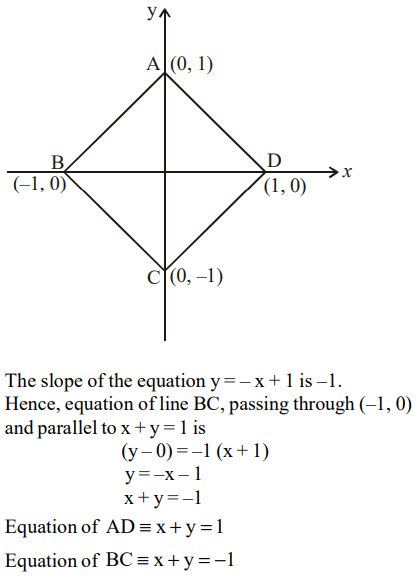
5. ABCD is a rhombus with diagonals AC and BD intersecting at the origin on the xy plane. If the equation of the line AD is
x + y = 1 then the equation of line BC is
a) x + y =1
b) x + y =-1
c) x - y =1
d) None of these
Explanation:
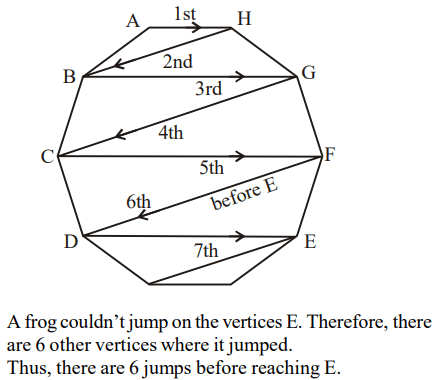
6. There is a regular octagon A B C D E F G H, a frog is at the vertex A. It can jump on to any of the vertices except the exactly opposite
vertex. The frog visits all the vertices exactly once and then reaches vertex E then how many times did it jump before reaching E?
a) 7
b) 2n + 1
c) 6
d) can’t be determined
Explanation:
7. If the perimeter of a triangle is 14 and the sides are integers, then how many different triangles are possible?
a) 6
b) 5
c) 4
d) 3
Explanation: a + b + c = 14 and c < a + b
Thus 2(a + b) > 14, a + b > 7
So, the possible measures of sides are (2, 6, 6), (3, 5, 6), (6, 4, 4) & (5, 5, 4).
Thus, there are four pairs possible.
8. a, b and c are sides of a triangle . If \[a^{2}+b^{2}+c^{2}=ab+bc+ac\] then the triangle will be
a) equilateral
b) isosceles
c) right angled
d) obtuse angle
Explanation:
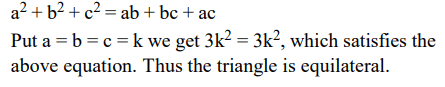
9. In triangle DEF shown below, points A, B, and C are taken on DE, DF and EF respectively such that EC = AC and CF = BC. If angle
D = 40 degrees then what is angle ACB in degrees?
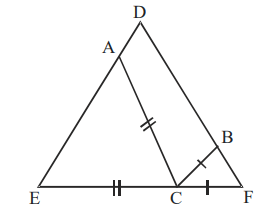
a) 140
b) 70
c) 100
d) None of these
Explanation:
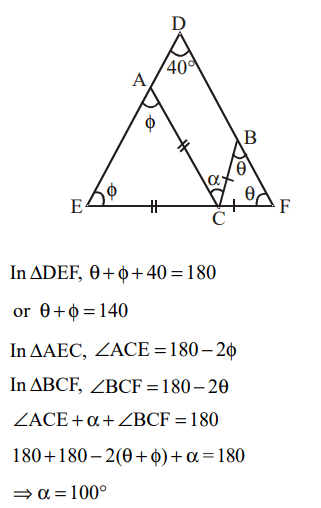
10. Based on the figure below, what is the value of x, if y = 10
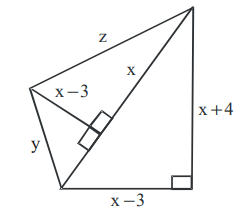
a) 10
b) 11
c) 12
d) None of these
Explanation:
