Data for Questions 1 & 2 : In the Indian athletic squad sent to the Olympics, 21 athletes were in the triathlon team; 26 were in the pentathlon team; and 29 were in the marathon team. 14 athletes can take part in triathlon and pentathlon; 12 can take part in marathon and triathlon; 15 can take part in pentathlon and marathon; and 8 can take part in all the three games.
1. How many players are there in all?
a) 35
b) 43
c) 49
d) none of these
Explanation: Since there are 14 who are in triathlon and pentathlon, and there are 8 who take part in all three games, there will be 6 who take part in only triathlon and pentathlon.
Similarly, Only triathlon and marathon = 12 – 8 = 4 & Only Pentathlon and Marathon = 15 – 8 = 7
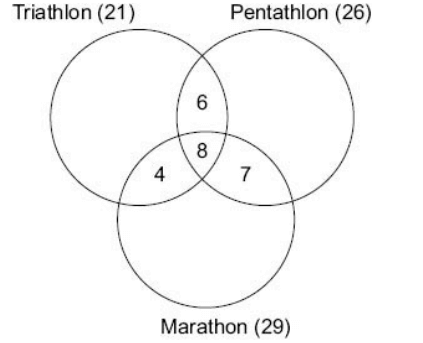
The figure above can be completed with values for each sport (only) plugged in:
1) 3 + 6 + 8 + 4 + 5 + 7 + 10 = 43
2. How many were in the marathon team only?
a) 10
b) 14
c) 18
d) 15
Explanation:

2) 29 - ( 4 + 8 + 7) = 10
Data for Questions 3 & 4 : In a test in which 120 students appeared, 90 passed in History, 65 passed in Sociology and 75 passed in Political Science. 30 students passed in only one subject and 55 students in only two. 5 students passed no subjects.
3. How many students passed in all the three subjects?
a) 25
b) 30
c) 35
d) Data insufficient
Explanation:
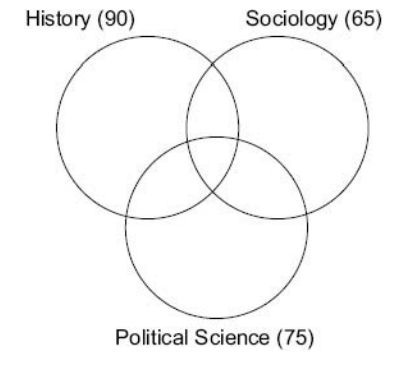
The given situation can be read as follows:
115 students are being counted 75 + 65 + 90 = 230 times.
This means that there is an extra count of 115. This extra count of 115 can be created in 2 ways.
A. By putting people in the ‘passed exactly two subjects’ category. In such a case each person would get counted 2 times (double counted), i.e., an extra count of 1.
B. By putting people in the ‘all three’ category, each person put there would be triple counted. 1 person counted 3 times – meaning an extra count of 2 per person.
The problem tells us that there are 55 students who passed exactly two subjects. This means an extra count of 55 would be accounted for. This would leave an extra count of 115–55 = 60 more to be accounted for by ‘passed all three’ category. This can be done by using 30 people in the ‘all 3’ category.
4. Find the number of students who passed in at least two subjects.
a) 85
b) 95
c) 90
d) Data insufficient
Explanation: 85 (Refer Explanation of Question 3)
Data for Questions 5 to 8 : 5% of the passengers who boarded Guwahati- New Delhi Rajdhani Express on 20th February, 2002 do not like coffee, tea and ice cream and 10% like all the three. 20% like coffee and tea, 25% like ice cream and coffee and 25% like ice cream and tea. 55% like coffee, 50% like tea and 50 % like ice cream.
5. The number of passengers who like only coffee is greater than the passengers who like only
ice cream by
a) 50%
b) 100%
c) 25%
d) 0
Explanation:
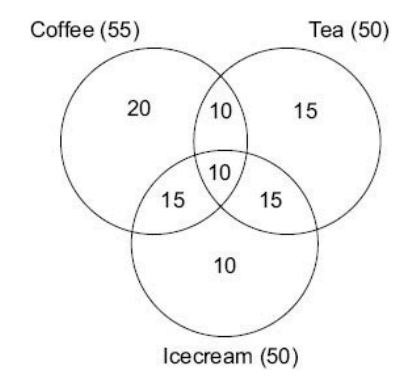
[(20 – 10)/10] * 100 = 100%.
Option (b) is correct
6. The percentage of passengers who like both tea and ice cream but not coffee is
a) 15
b) 5
c) 10
d) 25
Explanation:

15% (from the figure).
Option (a) is correct.
7. The percentage of passengers who like at least 2 of the 3 products is
a) 40
b) 45
c) 50
d) 60
Explanation: 10+10+15+15=50%.
Option (c) is correct
8. If the number of passengers is 180, then the number of passengers who like ice cream only is
a) 10
b) 18
c) 27
d) 36
Explanation: Only ice cream is 10% of the total. Hence, 10% of 180 = 18.
Option (b) is correct