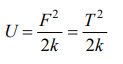1. A spring of force constant 800 N/m has an extension of 5cm. The work done in extending it
from 5cm to 15 cm is
a) 16 J
b) 8 J
c) 32 J
d) 24 J
Explanation:
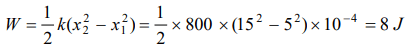
2. A spring when stretched by 2 mm its potential energy becomes 4 J. If it is stretched by 10 mm,its potential energy is equal to
a) 4 J
b) 54 J
c) 415 J
d) None
Explanation:
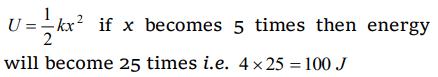
3. A spring of spring constant \[5\times10^{3}\] N/m is stretched initially by 5cm from the unstretched position. Then the work required to stretch it
further by another 5cm is
a) 6.25 N-m
b) 12.50 N-m
c) 18.75 N-m
d) 25.00 N-m
Explanation:
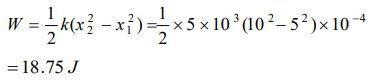
4. A mass of 0.5kg moving with a speed of 1.5 m/s on a horizontal smooth surface, collides with a nearly weightless spring of force constant \[K=50\] N/m. The maximum compression of the
spring would be
a) 0.15 m
b) 0.12 m
c) 1.5 m
d) 0.5 m
Explanation:
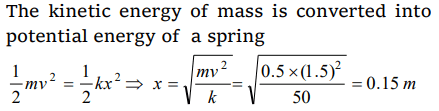
5. A particle moves in a straight line with retardation proportional to its displacement. Its loss of kinetic energy for any displacement x is
proportional to
a) \[x^{2}\]
b) \[e^{x}\]
c) x
d) \[log_{e}x\]
Explanation:

6.A spring with spring constant k when stretched through 1 cm, the potential energy is U. If it is stretched by 4 cm. The potential energy will be
a) 4U
b) 8U
c) 16 U
d) 2U
Explanation:
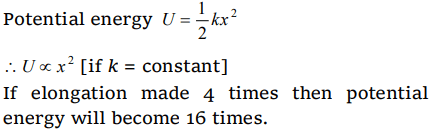
7. A spring with spring constant k is extended from \[x =0\] to \[x =x_{1}\] . The work done will be,
a) \[kx_1^2\]
b) \[\frac{1}{2}kx_1^2\]
c) \[2kx_1^2\]
d) \[2kx_1\]
Explanation: \[\frac{1}{2}kx_1^2\]
8. If a long spring is stretched by 0.02 m, its potential energy is U. If the spring is stretched by 0.1 m, then its potential energy will be
a) \[\frac{U}{5}\]
b) U
c) 5U
d) 25U
Explanation:
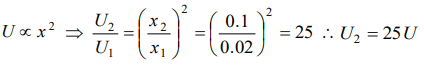
9. Natural length of a spring is 60 cm, and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is,
(Take g=9.8 \[m \diagup s ^{2}\] )
a) 4.9 cm
b) 0.49 cm
c) 9.4 cm
d) 0.94 cm
Explanation:
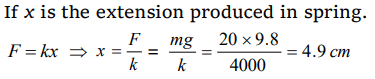
10. The spring extends by x on loading, then energy stored by the spring is :
(if T is the tension in spring and k is spring constant)
a) \[\frac{T^{2}}{2k}\]
b) \[\frac{T^{2}}{2k^{2}}\]
c) \[\frac{2k}{T^{2}}\]
d) \[\frac{2T^{2}}{k}\]
Explanation: