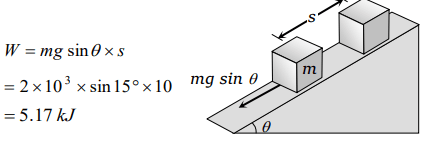
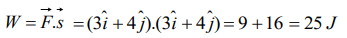1. The work done in pulling up a block of wood weighing 2 kN for a length of 10m on a smooth plane inclined at an angle of 15° with the
horizontal is
a) 4.36 kJ
b) 5.17 kJ
c) 8.91 kJ
d) 9.82 kJ
Explanation:
2. A force \[\overrightarrow{F} = 5\hat{i}+6\hat{j}-4\hat{k}\] acting on a body, produces a displacement \[\overrightarrow{s} = 6\hat{i}+5\hat{k}\] . Work done by the force is
a) 18 units
b) 15 units
c) 12 units
d) 10 units
Explanation:
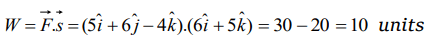
3. A force of 5 N acts on a 15 kg body initially at rest. The work done by the force during the first second of motion of the body is
a) 5 J
b) \[\frac{5}{6}J\]
c) 6 J
d) 75 J
Explanation:
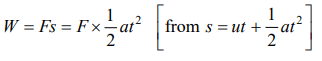
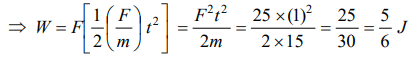
4. A force of 5 N, making an angle \[\theta\] with the horizontal, acting on an object displaces it by 0.4m along the horizontal direction. If the object gains kinetic energy of 1J, the horizontal
component of the force is
a) 1.5 N
b) 2.5 N
c) 3.5 N
d) 4.5 N
Explanation:
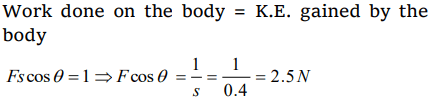
5.The work done against gravity in taking 10 kg mass at 1m height in 1sec will be
a) 49 J
b) 98 J
c) 196 J
d) None of these
Explanation: Work done = mgh = 10 * 9.8 * 1 = 98 J
6. The energy which an \[e^{-}\] acquires when accelerated through a potential difference of 1 volt is called
a) 1 Joule
b) 1 Electron volt
c) 1 Erg
d) 1 Watt
Explanation: 1 Electron volt
7. A body of mass 6kg is under a force which causes displacement in it given by \[S=\frac{t^{2}}{4}\] metres where t is time. The work done by the force in 2 seconds is,
a) 12 J
b) 9 J
c) 6 J
d) 3 J
Explanation:
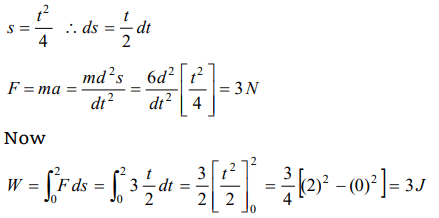
8. A body of mass 10kg at rest is acted upon simultaneously by two forces 4 N and 3N at right angles to each other. The kinetic energy of the body at the end of 10 sec is
a) 100 J
b) 300 J
c) 50 J
d) 125 J
Explanation:
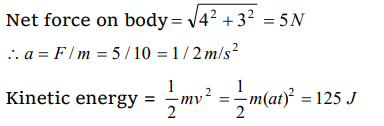
9.A cylinder of mass 10kg is sliding on a plane with an initial velocity of 10m/s. If coefficient of friction between surface and cylinder is 0.5, then
before stopping it will describe
a) 12.5 m
b) 5 m
c) 7.5 m
d) 10 m
Explanation:
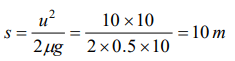
10. A force of ( \[3\hat{i}+4\hat{j}\] ) Newton acts on a body and displaces it by ( \[3\hat{i}+4\hat{j}\] ) m. The work done by the force is
a) 10 J
b) 12 J
c) 16 J
d) 25 J
Explanation: