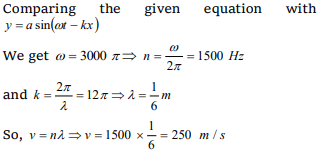1. The equation of a longitudinal wave is
represented as \[Y =20\cos \pi \left(50 t-x\right)\] . Its wavelength
is
a) 5 cm
b) 2 cm
c) 50 cm
d) 20 cm
Explanation:
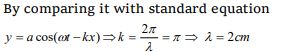
2. A wave equation which gives the displacement
along y-direction is given by y = 0.001 sin(100 t + x)
where x and y are in meterand t is time in second.
This represented a wave
a) Of frequency \[\frac{100}{\pi} Hz\]
b) Of wavelength one metre
c) Travelling with a velocity of \[\frac{50}{\pi} ms^{-1}\] in the
positive X-direction
d) Travelling with a velocity of \[100 ms^{-1}\] in the
negative X-direction
Explanation:
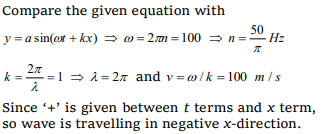
3.A transverse wave is given by \[Y =A\sin 2 \pi \left(\frac{t}{T}-\frac{x}{\lambda}\right)\] .
The maximum particle velocity is equal to 4 times
the wave velocity when
a) \[\lambda = 2 \pi A\]
b) \[\lambda =\frac{1}{2}\pi A\]
c) \[\lambda = \pi A\]
d) \[\lambda =\frac{1}{4}\pi A\]
Explanation:

4. The equation of a wave is represented by \[Y =10^{-4}\sin \left(100 t-\frac{x}{10}\right)\] . The velocity of the wave
will be
a) 100 m/s
b) 250 m/s
c) 750 m/s
d) 1000 m/s
Explanation:
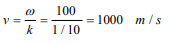
5. A wave travelling in positive X-direction with
\[A = 0.2m\] has a velocity of 360 m/sec. if \[\lambda = 60m\] ,
then correct expression for the wave is
a) \[Y =0.2\sin\left[ 2 \pi \left(6 t+\frac{x}{60}\right)\right]\]
b)\[Y =0.2\sin\left[ \pi \left(6 t+\frac{x}{60}\right)\right]\]
c) \[Y =0.2\sin\left[ 2 \pi \left(6 t-\frac{x}{60}\right)\right]\]
d) \[Y =0.2\sin\left[ \pi \left(6 t-\frac{x}{60}\right)\right]\]
Explanation:
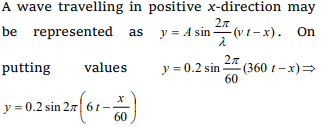
6. The equation of a wave motion (with t in seconds
and x in metres) is given by \[Y =7\sin \left(7\pi t-0.4\pi x+\frac{\pi}{3}\right)\] . The velocity of the wave
will be
a) 17.5 m/s
b) \[49\pi\] m/s
c) \[\frac{49}{2\pi}\] m/s
d) \[\frac{2\pi}{49}\] m/s
Explanation:
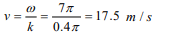
7. Two waves represented by the following
equations are travelling in the same medium \[Y_{1} =5\sin 2 \pi \left(75 t-0.25 x\right),Y_{2} =10\sin 2 \pi \left(150 t-0.50 x\right)\]
The intensity ratio I1 / I2 of the two waves is
a) 1 : 2
b) 1 : 4
c) 1 : 8
d) 1 : 16
Explanation:

8.The equation of a progressive wave is \[Y =8\sin \left[ \pi \left(\frac{t}{10}-\frac{x}{4}\right)+\frac{\pi}{3}\right]\] The wavelength of the
wave is
a) 8 m
b) 4 m
c) 2 m
d) 10 m
Explanation:
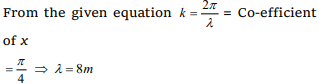
9.Which of the following is not true for this
progressive wave \[Y =4\sin 2 \pi \left(\frac{t}{0.02}-\frac{x}{100}\right)\] where y
and x are in cm & t in sec
a) Its amplitude is 4 cm
b) Its wavelength is 100 cm
c) Its frequency is 50 cycles/sec
d) Its propagation velocity is \[50 \times10^{3}cm/sec\]
Explanation:

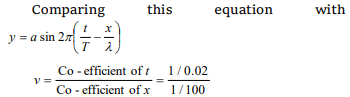
10.The equation of a wave is given as \[Y =0.07\sin \left(12\pi x-3000\pi t\right)\] . Where x is in metre and
t in sec, then the correct statement is
a) \[\lambda\] =1/ 6m, v = 250m/ s
b) a =0.07m, v = 300m/ s
c) n =1500m, v = 200m/ s
d) None
Explanation: