1. Equation of a progressive wave is given by
\[y=0.2\cos \pi\left(0.04 t+0.02x-\frac{\pi}{6}\right)\]
The distance is expressed in cm and time in
second. What will be the minimum distance
between two particles having the phase difference
of \[\pi/2\]
a) 4 cm
b) 8 cm
c) 25 cm
d) 12.5 cm
Explanation:

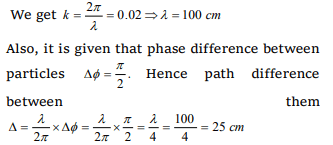
2. A travelling wave passes a point of observation.
At this point, the time interval between successive
crests is 0.2 seconds and
a) The wavelength is 5 m
b) The frequency is 5 Hz
c) The velocity of propagation is 5 m/s
d) The wavelength is 0.2 m
Explanation:

3.The equation of a transverse wave is given by
\[y=10\sin \pi\left(0.01x - 2t\right)\]
where x and y are in cm and t is in second. Its
frequency is
a) 10 \[sec^{-1}\]
b) 2 \[sec^{-1}\]
c) 1 \[sec^{-1}\]
d) 0.01 \[sec^{-1}\]
Explanation:

4. At a moment in a progressive wave, the phase of a
particle executing S.H.M. is \[\frac{\pi}{3}\] . Then the phase of
the particle 15 cm ahead and at the time \[\frac{T}{2}\]
will be, if the wavelength is 60 cm
a) \[\frac{\pi}{3}\]
b) \[\frac{2\pi}{3}\]
c) Zero
d) \[\frac{5\pi}{6}\]
Explanation:

5. The equation of a wave travelling on a string is \[y=4\sin \frac{\pi}{2}\left(8t - \frac{x}{8}\right)\] . If x and y are in cm, then
velocity of wave is
a) 64 cm/sec in – x direction
b) 32 cm/sec in – x direction
c) 32 cm/sec in + x direction
d) 64 cm/sec in + x direction
Explanation:
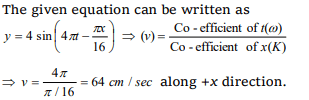
6. The equation of a progressive wave is given by
\[y=a\sin \left(628 t - 31.4x\right)\]
If the distances are expressed in cms and time in
seconds, then the wave velocity will be
a) 314 cm/sec
b) 628 cm/sec
c) 20 cm/sec
d) 400 cm/sec
Explanation:
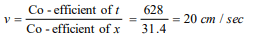
7. Two waves are given by \[y_{1}=a\sin \left(\omega t - kx\right)\] and
\[y_{2}=a\cos\left(\omega t - kx\right)\] . The phase difference between
the two waves is
a) \[\frac{\pi}{4}\]
b) \[\pi\]
c) \[\frac{\pi}{8}\]
d) \[\frac{\pi}{2}\]
Explanation:

8.If amplitude of waves at distance r from a point
source is A, the amplitude at a distance 2r will be
a) 2A
b) A
c) A/4
d) A/2
Explanation:
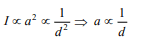
9.The relation between time and displacement for
two particles is given by
\[y_{1}=0.06\sin2\pi\left(0.04t +\phi_{1} \right),y_{2}=0.03\sin2\pi\left(1.04t +\phi_{2} \right)\]
The ratio of the intensity of the waves produced
by the vibrations of the two particles will be
a) 2 : 1
b) 1 : 2
c) 4 : 1
d) 1 : 4
Explanation:

10.A wave is reflected from a rigid support. The
change in phase on reflection will be
a) \[\pi/4\]
b) \[\pi/2\]
c) \[\pi\]
d) \[2\pi\]
Explanation: After reflection from rigid support, a wave suffers a phase change of \[\pi\]