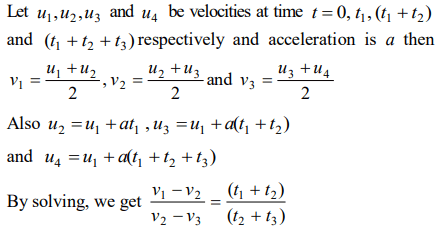1. The displacement x of a particle along a straight line at time t is given by \[X=a_{0}+a_{1}t+a_{2}t^{2}\] . The acceleration of the particle is
a) \[a_{0}\]
b) \[a_{1}\]
c) \[2a_{2}\]
d) \[a_{2}\]
Explanation:
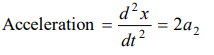
2. The coordinates of a moving particle at any time are given by \[X=at^{2}\] and \[Y=bt^{2}\] . The speed of the particle at any moment is
a) \[2t\left(a+b\right)\]
b) \[2t\sqrt{\left(a^{2}-b^{2}\right)}\]
c) \[t\sqrt{a^{2}+b^{2}}\]
d) \[2t\sqrt{\left(a^{2}+b^{2}\right)}\]
Explanation:
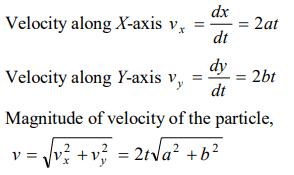
3. An electron starting from rest has a velocity that increases linearly with the time that is , \[v=kt\] where \[K=2m\diagup sec ^{2}\] . The distance travelled in the
first 3 seconds will be
a) 9 m
b) 16 m
c) 27 m
d) 36 m
Explanation:
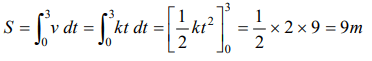
4. The displacement of a body is given to be proportional to the cube of time elapsed. The magnitude of the acceleration of the body is
a) Increasing with time
b) Decreasing with time
c) Constant but not zero
d) Zero
Explanation:
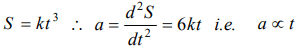
5. The instantaneous velocity of a body can be measured
a) Graphically
b) Vectorially
c) By speedometer
d) Both a and c
Explanation: Both a and c
6. A body is moving from rest under constant acceleration and let \[S_{1}\] be the displacement in the first \[\left(p-1\right)\] sec and \[S_{2}\] be the displacement in the
first p sec. The displacement in \[\left(p^{2}-p+1\right)^{th}\] sec. will be
a) \[S_{1}+S_{2}\]
b) \[S_{1}S_{2}\]
c) \[S_{1}-S_{2}\]
d) \[S_{1}\diagup S_{2}\]
Explanation:
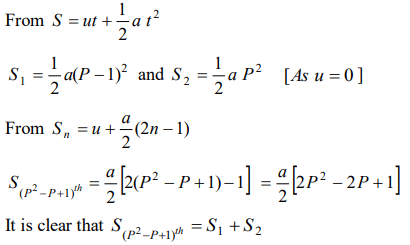
7. A body under the action of several forces will have zero acceleration
a) When the body is very light
b) When the body is very heavy
c) When the body is a point body
d) When the vector sum of all the forces acting on it is zero
Explanation:
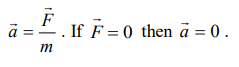
8. A body starts from the origin and moves along the X-axis such that the velocity at any instant is given by \[\left(4t^{3}-2t\right)\] , where t is in sec and velocity in m / s .
What is the acceleration of the particle, when it is 2 m from the origin
a) \[28m\diagup s^{2}\]
b) \[22m\diagup s^{2}\]
c) \[12m\diagup s^{2}\]
d) \[10m\diagup s^{2}\]
Explanation:
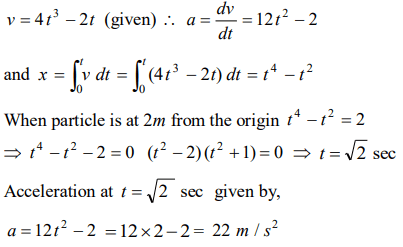
9. The relation between time and distance is \[t=\alpha x^{2}+\beta x\] , where \[\alpha\] and \[\beta\] are constants. The retardation is
a) \[2\alpha v^{3}\]
b) \[2\beta v^{3}\]
c) \[2\alpha\beta v^{3}\]
d) \[2\beta^{2} v^{3}\]
Explanation:
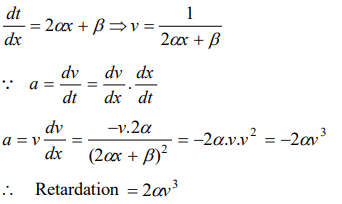
10. A point moves with uniform acceleration and \[v_{1}, v_{2} and v_{3}\] denote the average velocities in the three successive intervals of time \[t_{1}, t_{2} and t_{3}\] . Which of the following relations is correct
a) \[ \left(v_{1}-v_{2}\right):\left(v_{2}-v_{3}\right)=\left(t_{1}-t_{2}\right):\left(t_{2}+t_{3}\right)\]
b) \[ \left(v_{1}-v_{2}\right):\left(v_{2}-v_{3}\right)=\left(t_{1}+t_{2}\right):\left(t_{2}+t_{3}\right)\]
c) \[ \left(v_{1}-v_{2}\right):\left(v_{2}-v_{3}\right)=\left(t_{1}-t_{2}\right):\left(t_{1}-t_{3}\right)\]
d) \[ \left(v_{1}-v_{2}\right):\left(v_{2}-v_{3}\right)=\left(t_{1}-t_{2}\right):\left(t_{2}-t_{3}\right)\]
Explanation: