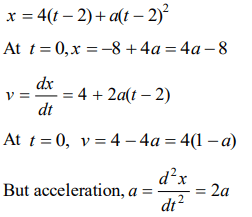1. An object accelerates from rest to a velocity 27.5 m/s in 10 sec then find distance covered by object in next 10 sec
a) 550 m
b) 137.5 m
c) 412.5 m
d) 275 m
Explanation:
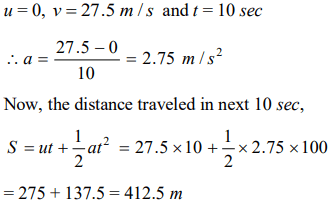
2. If the velocity of a particle is given by \[V=\left(180 -16 x\right)^{1/2}\] m/s, then its acceleration will be
a) Zero
b) \[8 m\diagup s^{2} \]
c) \[-8 m\diagup s^{2} \]
d) \[4 m\diagup s^{2} \]
Explanation:
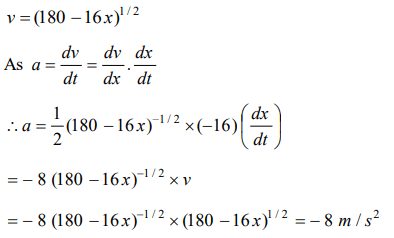
3. The displacement of a particle is proportional to the cube of time elapsed. How does the acceleration of the particle depends on time obtained
a) \[a \propto t^{2} \]
b) \[a \propto 2t \]
c) \[a \propto t^{3} \]
d) \[a \propto t \]
Explanation:
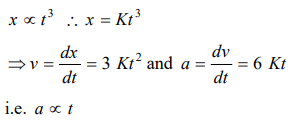
4. Starting from rest, acceleration of a particle is \[a =2\left(t-1\right)\] . The velocity of the particle at \[t =5s\] is
a) 15 m/sec
b) 25 m/sec
c) 5 m/sec
d) None of these
Explanation:
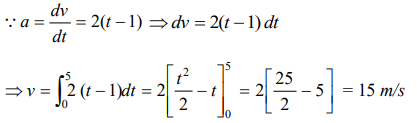
5. A body is moving with uniform acceleration describes 40 m in the first 5 sec and 65 m in next 5 sec. Its initial velocity will be
a) 4 m/s
b) 2.5 m/s
c) 5.5 m/s
d) 11 m/s
Explanation:
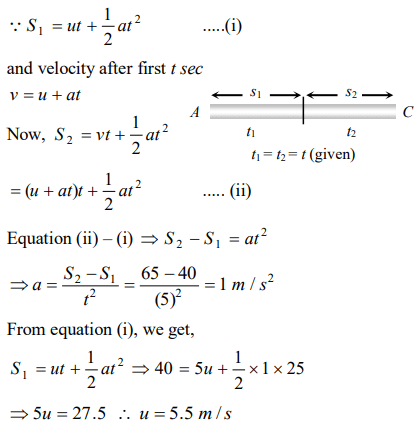
6. Speed of two identical cars are u and 4u at a specific instant. The ratio of the respective distances in which the two cars are stopped from that instant is
a) 1 : 1
b) 1 : 4
c) 1 : 8
d) 1 : 16
Explanation:
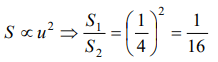
7. The displacement x of a particle varies with time \[t,x =ae^{-\alpha t}+be^{\beta t}\] , where \[a,b,\alpha\] and \[\beta\] are positive
constants. The velocity of the particle will
a) Go on decreasing with time
b) Be independent of \[\alpha\] and \[\beta\]
c) Drop to zero when \[\alpha =\beta\]
d) Go on increasing with time
Explanation:
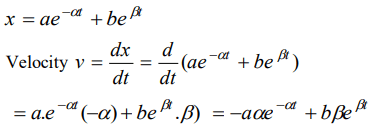
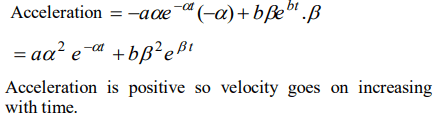
8. A car, starting from rest, accelerates at the rate f through a distance S, then continues at constant speed for time t and then decelerates at the rate
\[\frac{f}{2}\] to come to rest. If the total distance traversed is 15 S, then
a) \[S=\frac{1}{2}ft^{2}\]
b) \[S=\frac{1}{4}ft^{2}\]
c) \[S=\frac{1}{72}ft^{2}\]
d) \[S=\frac{1}{6}ft^{2}\]
Explanation: Let car starts from point A from rest and moves up to point B with acceleration f

9. A man is 45 m behind the bus when the bus start accelerating from rest with acceleration \[2.5m\diagup s^{2}\]. With what minimum velocity should the man start
running to catch the bus ?
a) 12 m/s
b) 14 m/s
c) 15 m/s
d) 16 m/s
Explanation:

10. A particle moves along x-axis as
\[x=4\left(t-2\right)+a\left(t-2\right)^{2}\]
Which of the following is true ?
a) The initial velocity of particle is 4
b) The acceleration of particle is 2a
c) The particle is at origin at t = 0
d) None of these
Explanation: