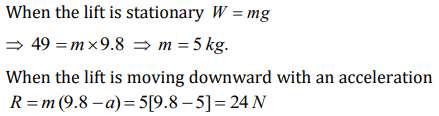1. A rocket is ejecting 50 g of gases per sec at a speed of 500 m/s. The accelerating force on the
rocket will be
a) 125 N
b) 25 N
c) 5 N
d) Zero
Explanation:
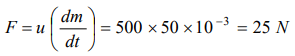
2. A block of mass 5 kg is moving horizontally at a speed of 1.5 m/s. A perpendicular force of 5N acts
on it for 4 sec. What will be the distance of the block from the point where the force started
acting
a) 10 m
b) 8 m
c) 6 m
d) 2 m
Explanation:
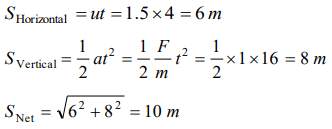
3. A lift of mass 1000 kg is moving with an acceleration of \[1 m\diagup s^{2}\] in upward direction.
Tension developed in the string, which is connected to the lift, is
a) 9,800 N
b) 10,000 N
c) 10,800 N
d) 11,000 N
Explanation: T = m(g + a) = 1000(9.8 +1) = 10800 N
4. A lift accelerated downward with acceleration 'a'. A man in the lift throws a ball upward with acceleration \[a_{0}\left(a_{0}<a\right)\] . Then acceleration of ball
observed by observer, which is on earth, is
a) \[\left(a+a_{0}\right)\] upward
b) \[\left(a-a_{0}\right)\] upward
c) \[\left(a+a_{0}\right)\] downward
d) \[\left(a-a_{0}\right)\] downward
Explanation: The effective acceleration of ball observed by observer on earth = (a – a0)
As a0 < a, hence net acceleration is in downward direction.
5. A lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in
the lift and a man standing stationary on the ground are respectively
a) \[g,g\]
b) \[g-a,g-a\]
c) \[g-a,g\]
d) \[a,g\]
Explanation: Due to relative motion, acceleration of ball observed by observer in lift = (g – a) and for man on earth the acceleration remains g.
6. A man weighs 80kg He stands on a weighing scale in a lift which is moving upwards with a uniform acceleration of \[5 m\diagup s^{2}\] . What would be the
reading on the scale. \[\left(g=10 m\diagup s^{2}\right)\]
a) 400 N
b) 800 N
c) 1200 N
d) Zero
Explanation: For accelerated upward motion R = m(g + a) = 80 (10 + 5) = 1200 N
7. A monkey of mass 20kg is holding a vertical rope. The rope will not break when a mass of 25 kg is suspended from it but will break if the mass
exceeds 25 kg. What is the maximum acceleration with which the monkey can climb up along the rope\[\left(g=10 m\diagup s^{2}\right)\]
a) \[10 m\diagup s^{2}\]
b) \[25 m\diagup s^{2}\]
c) \[2.5 m\diagup s^{2}\]
d) \[5 m\diagup s^{2}\]
Explanation: Tension the string = m(g + a) = Breaking force
20(g + a) = 25 * g
a = g / 4 = 2.5 m / s2
8. If in a stationary lift, a man is standing with a bucket full of water, having a hole at its bottom. The rate of flow of water through this hole is . \[R_{0}\]
If the lift starts to move up and down with same acceleration and then that rates of flow of water are \[R_{u}\] and \[R_{d}\] , then
a) \[R_{0}>R_{u}>R_{d}\]
b) \[R_{u}>R_{0}>R_{d}\]
c) \[R_{d}>R_{0}>R_{u}\]
d) \[R_{u}>R_{d}>R_{0}\]
Explanation: Rate of flow will be more when lift will move in upward direction with some acceleration because the net downward pull will be more and vice-versa. Fupward = m (g + a) and Fdownward = m (g - a)
9. A rocket with a lift- off mass \[3.5 \times 10 ^{4}kg\] is blasted upwards with an initial acceleration of \[10 m\diagup s^{2}\] . Then the initial thrust of the blast is
a) \[1.75 \times10 ^{5}kg\]
b) \[3.5 \times10 ^{5}kg\]
c) \[7.0 \times10 ^{5}kg\]
d) \[14.0 \times10 ^{5}kg\]
Explanation:
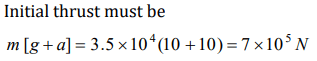
10. A spring balance is attached to the ceiling of a lift. A man hangs his bag on the spring and the spring reads 49 N, when the lift is stationary. If the lift
moves downward with an acceleration of \[5 m\diagup s^{2}\] , the reading of the spring balance will be
a) 49 N
b) 24 N
c) 74 N
d) 15 N
Explanation: