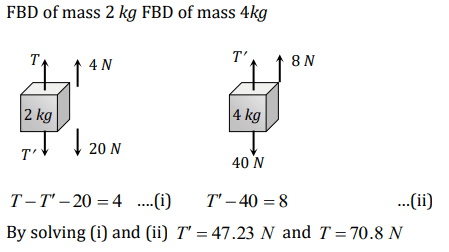1. Two forces of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
a) \[45^{\circ}\]
b) \[120^{\circ}\]
c) \[150^{\circ}\]
d) \[60^{\circ}\]
Explanation:
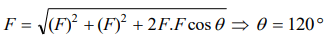
2. Two forces with equal magnitudes F act on a body and the magnitude of the resultant force is F/3.The angle between the two forces is
a) \[\cos^{-1}-\frac{17}{18}\]
b) \[\cos^{-1}-\frac{1}{3}\]
c) \[\cos^{-1}\frac{1}{3}\]
d) \[\cos^{-1}\frac{8}{9}\]
Explanation:
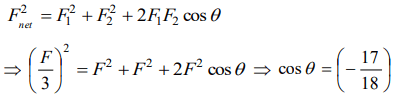
3. An object is subjected to a force in the north-east direction. To balance this force, a second force should be applied in the direction
a) North-East
b) South
c) South-West
d) West
Explanation: Direction of second force should be at 180°
4. The resultant force of 5 N and 10 N can not be
a) 12 N
b) 8 N
c) 4 N
d) 5 N
Explanation:
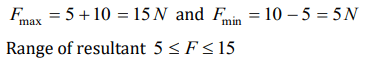
5. The resultant of two forces 3P and 2P is R. If the first force is doubled then the resultant is also doubled. The angle between the two forces is
a) \[60^{\circ}\]
b) \[120^{\circ}\]
c) \[70^{\circ}\]
d) \[180^{\circ}\]
Explanation:
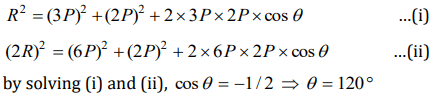
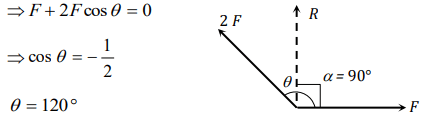
6. The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces. The angle between the two forces is
a) \[60^{\circ}\]
b) \[120^{\circ}\]
c) \[150^{\circ}\]
d) \[90^{\circ}\]
Explanation:
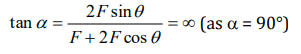
7. Two forces are such that the sum of their magnitudes is 18 N and their resultant is perpendicular to the smaller force and magnitude of resultant is 12 N. Then the magnitudes of the
forces are
a) 12 N, 6 N
b) 13 N, 5 N
c) 10 N, 8 N
d) 16 N, 2 N
Explanation:
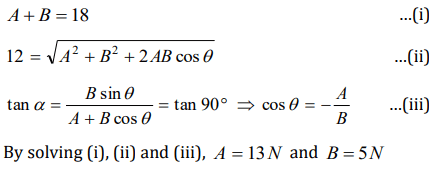
8. Three forces starts acting simultaneously on a particle moving with velocity \[\vec{v}\] . These forces are represented in magnitude and direction by the
three sides of a triangle ABC (as shown). The particle will now move with velocity
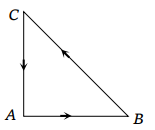
a) \[\vec{V}\] remaining unchanged
b) Less than \[\vec{V}\]
c) Greater than \[\vec{V}\]
d) \[\vec{V}\] in the direction of the largest force BC
Explanation: Net force on the particle is zero so the \[\vec{v}\] remains unchanged.
9. Which of the following groups of forces could be in equibrium
a) 3 N, 4 N, 5 N
b) 4N, 5 N, 10 N
c) 30N, 40 N, 80 N
d) 1N, 3 N, 5 N
Explanation: For equilibrium of forces, the resultant of two (smaller) forces should be equal and opposite to third one
10. Two blocks are connected by a string as shown in the diagram. The upper block is hung by another string. A force F applied on the upper string
produces an acceleration of \[2 m\diagup s^{2}\] in the upward direction in both the blocks. If T and \[T'\] be the tensions in the two parts of the string, then
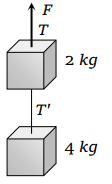
a) \[T= 70.8N\] and \[T' = 47.2N\]
b) \[T= 58.8N\] and \[T' = 47.2N\]
c) \[T= 70.8N\] and \[T' = 58.8N\]
d) \[T= 70.8N\] and \[T' = 0\]
Explanation: