1. The average power (Pavg) is expressed as?
a) Pasecθ
b) Patanθ
c) Pacosθ
d) Pasinθ
Explanation: The average power is the product of the apparent power and cosθ. The average power (Pavg) is expressed as Pacosθ. Average power = Pacosθ.
2. The equation of reactive power is?
a) Pacosθ
b) Pasecθ
c) Pasinθ
d) Patanθ
Explanation: The reactive power is the product of the apparent power and sinθ. The equation of reactive power is Pasinθ. Reactive power = Pasinθ
3. A sinusoidal voltage v = 50sinωt is applied to a series RL circuit. The current in the circuit is given by I = 25sin (ωt-53⁰). Determine the apparent power (VA).
a) 620
b) 625
c) 630
d) 635
Explanation: The expression of apparent power (VA) is Papp= VeffIeff = (Vm/√2)×(Im/√2). On substituting the values Vm = 50, Im = 25, we get apparent power = (50×25)/2 = 625VA.
4. A sinusoidal voltage v = 50sinωt is applied to a series RL circuit. The current in the circuit is given by I = 25sin (ωt-53⁰). Find the power factor.
a) 0.4
b) 0.5
c) 0.6
d) 0.7
Explanation:In sinusoidal sources the power factor is the cosine of the phase angle between the voltage and the current. The expression of power factor = cosθ = cos53⁰ = 0.6.
5. A sinusoidal voltage v = 50sinωt is applied to a series RL circuit. The current in the circuit is given by I = 25sin (ωt-53⁰). Determine the average power.
a) 365
b) 370
c) 375
d) 380
Explanation: The average power, Pavg = VeffIeffcosθ. We know the values of Veff, Ieff are Veff = 625 and Ieff – 0.6. So the average power = 625 x 0.6 = 375W
6. If there are M branch currents, then we can write ___________ number of independent equations.
a) M-2
b) M-1
c) M
d) M+1
Explanation: If there are M branch currents, then we can write M number of independent equations. Number of independent equations = M
7. f there are M meshes, B branches and N nodes including reference node, the number of mesh currents is given as M=?
a) B + (N+1)
b) B + (N-1)
c) B-(N+1)
d) B-(N-1)
Explanation: If there are M meshes, B branches and N nodes including reference node, the number of mesh currents is given as M = B-(N-1)
8. In the circuit shown below. Find the current I2.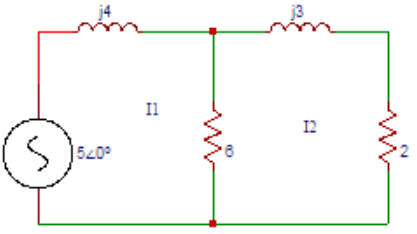
a) 0.5∠-90⁰
b) 0.6∠-90⁰
c) 0.7∠-90⁰
d) 0.8∠-90⁰
Explanation:The equation for loop 1 is I1(j4) + 6(I1-I2) = 5∠0⁰. The equation for loop 2 is 6(I1-I2) + (j3) I2 + (2) I2 = 0. Solving the above equations, I2 = 0.6∠-90⁰
9. Determine Z21, Z22, Z23 in the circuit shown below.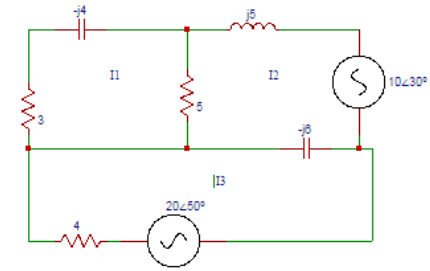
a) 5Ω, (5-j1) Ω, j6 Ω
b) -5Ω, (5-j1) Ω, j6 Ω
c) -5Ω, (5+j1) Ω, j6 Ω
d) -5Ω, (5-j1) Ω, – j6 Ω
Explanation: Z21 = common impedance to loop 1 and loop 2 = -5 Ω. Z22 = self impedance of loop2 = (5+j5-j6) Ω. Z23 = common impedance between loop2 and loop 3 = – (-j6) Ω.
10. Find Z31, Z32, Z33 in the circuit shown below.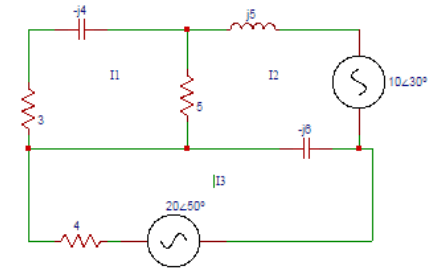
a) 0Ω, j6Ω, (4-j6) Ω
b) 0Ω, -j6Ω, (4+j6) Ω
c) 0Ω, -j6Ω, (4-j6) Ω
d) 0Ω, j6Ω, (4+j6) Ω
Explanation: Z31 = common impedance to loop 3 and loop 1 = 0 Ω. Z32 = common impedance between loop3 and loop 2 = – (-j6) Ω. Z33 = self impedance of loop 3 = (4-j6) Ω.