1. Which of the following is the difference equation of a special case of FIR system?
a) y(n) = \(\sum_{k=0}^{M} b_k x(n-k)\)
b) y(n) = \(a_0y(n)-\sum_{k=1}^{N} a_k y(n-k)\)
c) y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)\)
d) None of the above
Explanation: If the coefficients of the past values of the output in the difference equation of the system, then the system is said to be FIR system.
2. What is the form of the FIR system to compute the moving average of the signal x(n)?
a) y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n+k)\)
b) y(n)=\(\frac{1}{M+1} \sum_{k=0}^{\infty} x(n-k)\)
c) y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n-k)\)
d) None of the mentioned
Explanation: A normal FIR non-recursive system with the impulse response h(n)=\(\frac{1}{M+1}\) is the system which is used to compute the moving average of a signal x(n).
3. To implement the linear time invariant recursive system described by the difference equation y(n)=\(-\sum_{k=1}^N a_k y(n-k)+\sum_{k=0}^M b_k x(n-k)\) in Direct form-I, how many number of delay elements and multipliers are required respectively?
a) M+N-1, M+N
b) M+N, M+N+1
c) M+N+1, M+N
d) None of the mentioned
Explanation: From the given equation, there are M+N delays, so it requires M+N number of delay elements and it has to perform M+N+1 multiplications, so it require that many number of multipliers.
4. The system represented by the following direct form structure is: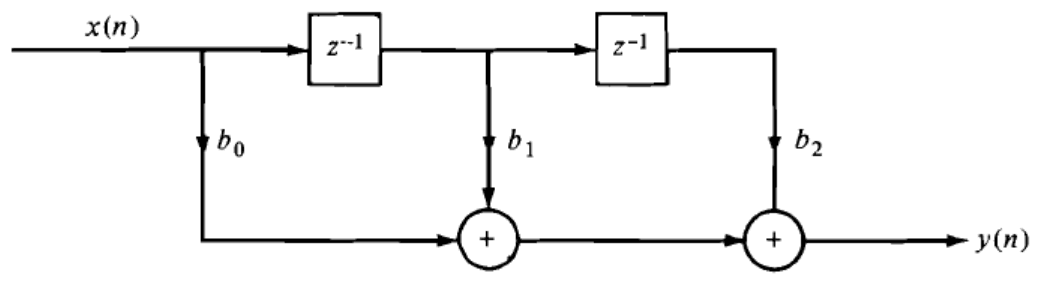
a) General second order system
b) Partial recursive system
c) Purely recursive system
d) FIR system
Explanation: The output of the system according to the direct form given is
y(n)= b0x(n)+b1x(n-1)+b2x(n-2)
Since the output of the system is purely dependent on the present and past values of the input, the system is called as FIR system.
5. The system described by the equation y(n)=ay(n-1)+bx(n) is a recursive system.
a) True
b) False
Explanation: Since the present output depends on the value of the previous output, the system is called a Recursive system.
6. Zero-state response is also known as ____________
a) Forced response
b) Natural response
c) Free response
d) None of the mentioned
Explanation: The zero-state response depends on the nature of the system and the input signal. Since this output is a response forced upon it by the input signal, it is also known as Forced response.
7. Which of the following is a recursive form of a non-recursive system described by the equation y(n)=\(\frac{1}{M+1} \sum_{k=0}^Mx(n-k)\)?
a) y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1-M)]
b) y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)+x(n-1+M)]
c) y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1+M)]
d) y(n)=y(n-1)+\(\frac{1}{M+1}\)[x(n)-x(n-1-M)]
Explanation: y(n)=\(\frac{1}{M+1} \sum_{k=0}^M x(n-k)\)
It can be expressed as -
\(y(n)=\frac{1}{M+1} \sum_{k=0}^M x(n-1-k)+\frac{1}{M+1}[x(n)-x(n-1-M)]\)
=\(y(n-1)+\frac{1}{M+1}[x(n)-x(n-1-M)]\)
8. What is the output of the system represented by the following direct form?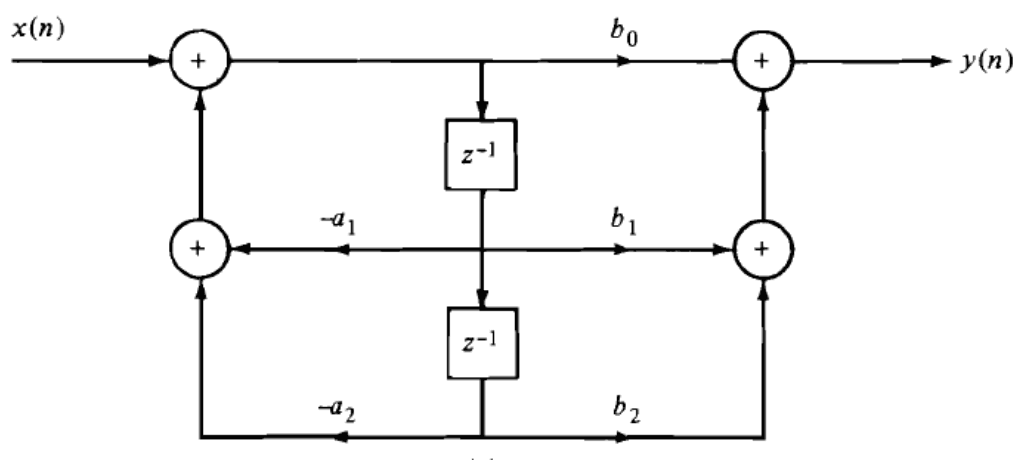
a) y(n)=-a1y(n-1)-a2y(n-2)- b0x(n)-b1x(n-1)-b2x(n-2)
b) y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)
c) y(n)=-a1y(n-1)-a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)
d) y(n)=a1y(n-1)+a2y(n-2)+ b0x(n)+b1x(n-1)+b2x(n-2)
Explanation: The equation of the difference equation of any system is defined as
y(n)=\(-\sum_{k=1}^Na_k y(n-k)+\sum_{k=0}^{M}b_k x(n-k)\)
In the given diagram, N=M=2
We get, y(n)=-a1y(n-1)-a2y(n-2)+b0x(n)+b1x(n-1)+b2x(n-2)
9. An FIR system is also called as “recursive system”.
a) True
b) False
Explanation: For a system to be recursive, the output of the system must be dependent only on the past values of the output. For an FIR system the output of the system must be depending only on the present and past values of the input. So, FIR system is not an recursive system.
10. Which of the following linear time invariant system is a purely recursive system?
a) y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)-\sum_{k=0}^{M} b_k x(n-k)\)
b) y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)
c) y(n) = \(\sum_{k=1}^{N} a_k y(n-k)+\sum_{k=0}^{M} b_k x(n-k)\)
d) y(n) = \(-\sum_{k=1}^{N} a_k y(n-k)+b_0x(n)\)
Explanation: Since the output of the system depend only on the past values of output and the present value of the input, the system is called as purely recursive system.