1. The resistance can be measured most accurately by _________
a) Voltmeter-Ammeter method
b) Bridge method
c) Multimeter
d) Megger
Explanation: Bridge method applies the concept of null point or bridge balance condition. Multimeter and Megger are used for measuring very high resistances and Voltmeter-Ammeter method is used for Low resistances. A null type instrument has higher accuracy as compared to a deflection type instrument
2. A slide wire potentiometer has 10 wires of 2 m each. With the help of a standard voltage source of 1.045 V, it is standardized by keeping the jockey at 104.5 cm. If the resistance of potentiometer wires is 2000 Ω, then the value of working current is?
a) 1 mA
b) 10 mA
c) 0.1 mA
d) 0.5 mA
Explanation: Total length of the slide wire = 10 × 200
Total resistance of slide wire = 2000 Ω
∴ Resistance per cm = 1 Ω
Resistance of 104.5 cm = 104.5 Ω
This corresponds to a voltage of 1.045 V
∴ Current = \(\frac{1.045}{104.5}\) = 10 mA.
3. Which of the following method is used for the measurement of Medium Resistance?
a) Kelvin’s double bridge method
b) Carey-Foster bridge method
c) Anderson Bridge
d) Direct-Deflection method
Explanation:Kelvin’s double bridge method is used for measurement of Low Resistance, Anderson Bridge is not used for measurement of Resistance and Direct-Deflection method is used for Measurement of High Resistance
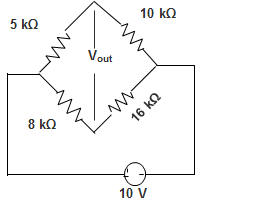
4. In the Wheatstone bridge shown below, if the resistance in each arm is increased by 0.05%, then the value of Vout will be ________
a) 50 mV
b) Zero
c) 5mV
d) 0.1mV
Explanation: In Wheatstone bridge, balance condition is
R1R3 = R2R4
Here, R1 = 5, R2 = 10, R3 = 16, R4 = 8
And when the Wheatstone bridge is balanced then, at Vout voltage will be Zero.
5. A resistor of 10 kΩ with the tolerance of 5% is connected in parallel with 5 kΩ resistors of 10% tolerance. What is the tolerance limit for a parallel network?
a) 9%
b) 12.4%
c) 8.33%
d) 7.87%
Explanation: Here, R1 and R2 are in parallel.
Then, \(\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\)
Or, R = \(\frac{50}{15}\) kΩ
∴\( \frac{△R}{R} = \frac{△R_1}{R_1^2} + \frac{△R_2}{R_2^2}\)
And △R1 = 0.5×103, △R2 = 0.5×103
∴\( \frac{△R}{R} = \frac{10 × 10^3}{3 × 10 × 10^3} × \frac{0.5 × 10^3}{10 × 10^3} + \frac{10}{3} × \frac{10^3}{5 × 10^3} × \frac{0.5 × 10^3}{5 × 10^3}\)
= \( \frac{0.5}{30} + \frac{1}{15} = \frac{2.5}{30}\) = 8.33%
6. A 0-400V voltmeter has a guaranteed accuracy of 1% of full scale reading. The voltage measured by this instrument is 250 V. Calculate the limiting error in percentage.
a) 4%
b) 2%
c) 2.5%
d) 1%
Explanation: The magnitude of limiting error of the instrument
ρA = 0.01 × 400 = 4 V
The magnitude of voltage being measured = 250 V
The relative at this voltage Er = \( \frac{4}{250}\) = 0.016
∴ Voltage measured is between the limits
Aa = As(1± Er)
= 250(1 ± 0.016)
= 250 ± 4 V
7. The current flowing in a resistor of 1Ω is measured to be 25 A. But it was discovered that ammeter reading was low by 1% and resistance was marked high by 0.5%. Find true power as a percentage of the original power.
a) 95%
b) 101.5%
c) 100.1%
d) 102.4%
Explanation:True current = 25(1 + 0.01) = 25.25 A
True resistance R = 1(1 – 0.005) = 0.995Ω
∴ True power = I2R = 634.37 W
Measured power = (25)2 × 1 = 625 W
∴ \( \frac{True \,power}{Measured \,power}\) × 100 = \(\frac{634.37}{625}\) × 100 = 101.5%.
8. A resistor of 10 kΩ with the tolerance of 5% is connected in series with 5 kΩ resistors of 10% tolerance. What is the tolerance limit for a series network?
a) 9%
b) 12.04%
c) 8.67%
d) 6.67%
Explanation: Error in 10 kΩ resistance = 10 × \( \frac{5}{100}\) = 0.5 kΩ
Error in 5 kΩ resistance = 5 × \( \frac{10}{100}\) = 5 kΩ
Total measurement resistance = 10 + 0.5 + 5 + 0.5 = 16 kΩ
Original resistance = 10 + 5 = 15 kΩ
Error = \( \frac{16-15}{15}\) × 100 = \( \frac{1}{15}\) × 100 = 6.67%.
9. Two resistances 100 ± 5Ω and 150 ± 15Ω are connected in series. If the error is specified as standard deviations, the resultant error will be _________
a) ±10 Ω
b) ±10.6 Ω
c) ±15.8 Ω
d) ±20 Ω
Explanation: Given, R1 = 100 ± 5 Ω
R2 = 150 ± 15 Ω
Now, R = R1 + R2
The probable errors in this case, R = \( ± (R_1^2 + R_2^2 )^{0.5}\) = ± 15.8 Ω.
10. Resistances R1 and R2 have respectively, nominal values of 10Ω and 5Ω and limiting error of ± 5% and ± 10%. The percentage limiting error for the series combination of R1 and R2 is?
a) 6.67%
b) 5.5%
c) 7.77%
d) 2.8%
Explanation: R1 = 10 ± 5%
R2 = 5 ± 10%
R1 = 10 ± \( \frac{5}{100}\) × 10 = 10 ± 0.5Ω
R2 = 5 ± \( \frac{5}{100}\) × 5 = 5 ± 0.5Ω
The limiting value of resultant resistance = 15 ± 1
Percentage limiting error of series combination of resistance = \( \frac{1}{15}\) × 100 = 6.67%.