1. A block of mass m lying on a rough horizontal plane is acted upon by a horizontal force P and another force Q inclined at an angle \[\theta\] to the vertical. The block will remain in equilibrium, if
the coefficient of friction between it and the surface is
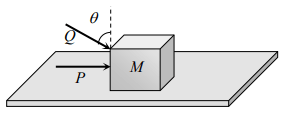
a) \[\frac{\left(P+Q\sin\theta\right)}{\left(mg+Q\cos\theta\right)}\]
b) \[\frac{\left(P\cos\theta+Q\right)}{\left(mg-Q\sin\theta\right)}\]
c) \[\frac{\left(P+Q\cos\theta\right)}{\left(mg+Q\sin\theta\right)}\]
d) \[\frac{\left(P\cos\theta-Q\right)}{\left(mg-Q\sin\theta\right)}\]
Explanation:
2. Which of the following is correct, when a person walks on a rough surface
a) The frictional force exerted by the surface keeps him moving
b) The force which the man exerts on the floor keeps him moving
c) The reaction of the force which the man exerts on floor keeps him moving
d) None of the above
Explanation: The reaction of the force which the man exerts on floor keeps him moving
3. A block of mass 0.1 kg is held against a wall by applying a horizontal force of 5 N on the block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of
the frictional force acting on the block is
a) 2.5 N
b) 0.98 N
c) 4.9 N
d) 0.49 N
Explanation:

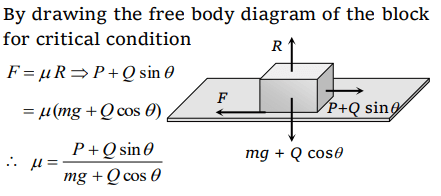
4.A body of mass M is kept on a rough horizontal surface (friction coefficient \[\mu\] ). A person is trying to pull the body by applying a horizontal force but the body is not moving. The
force by the surface on the body is F, where
a) \[F= Mg\]
b) \[F=\mu Mgf\]
c) \[ Mg\leq F\leq Mg\sqrt{1+\mu^{2}}\]
d) \[ Mg\geq F\geq Mg\sqrt{1+\mu^{2}}\]
Explanation:
5. What is the maximum value of the force F such that the block shown in the arrangement, does not move
a) 20 N
b) 10 N
c) 12 N
d) 15 N
Explanation:
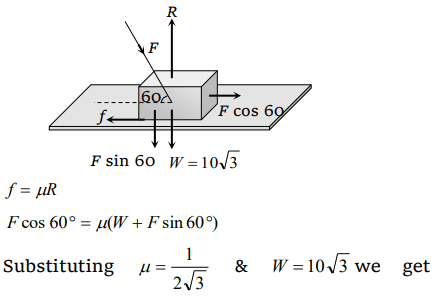
F = 20N
6. A block P of mass m is placed on a frictionless horizontal surface. Another block Q of same mass is kept on P and connected to the wall with the help of a spring of spring
constant k as shown in the figure. \[\mu_{s}\] is the coefficient of friction between P and Q. The blocks move together
performing SHM of amplitude A. The maximum value of the friction force between P and Q is
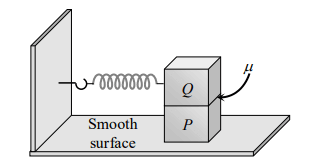
a) kA
b) \[\frac{kA}{2}\]
c) Zero
d) \[\mu_{s}mg\]
Explanation:

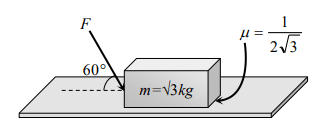
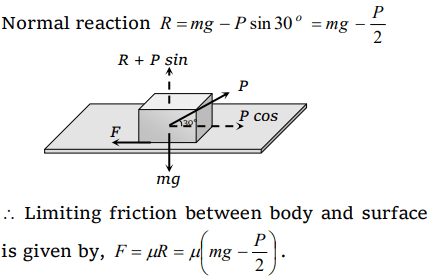
7. A body of mass m rests on horizontal surface. The coefficient of friction between the body and the surface is \[\mu\] . If the mass is pulled by a force P as shown in the figure, the limiting
friction between body and surface will be
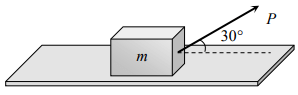
a) \[\mu mg\]
b) \[\mu \left[mg+\left(\frac{P}{2}\right)\right]\]
c) \[\mu \left[mg-\left(\frac{P}{2}\right)\right]\]
d) \[\mu \left[mg-\left(\frac{\sqrt{3}P}{2}\right)\right]\]
Explanation:
8.A 40 kg slab rests on a frictionless floor as shown in the figure. A 10 kg block rests on the top of the slab. The static coefficient of friction between the block and slab is 0.60 while the kinetic
friction is 0.40. The 10 kg block is acted upon by a horizontal force 100 N. If\[g=9.8m\diagup s^{2}\] , the resulting acceleration of the slab will be
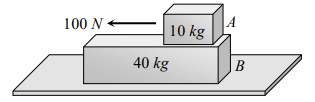
a) \[0.98m\diagup s^{2}\]
b) \[1.47m\diagup s^{2}\]
c) \[1.52m\diagup s^{2}\]
d) \[6.1m\diagup s^{2}\]
Explanation:

9. A block of mass 2 kg rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional
force on the block is
a) 9.8 N
b) \[0.7\times 9.8\times\sqrt{3}N\]
c) \[ 9.8\times\sqrt{3}N\]
d) \[0.8\times 9.8 N\]
Explanation:

10. When a bicycle is in motion, the force of friction exerted by the ground on the two wheels is such that it acts
a) In the backward direction on the front wheel and in the forward direction on the rear wheel
b) In the forward direction on the front wheel and in the backward direction on the rear wheel
c) In the backward direction on both front and the rear wheels
d) Both a and c
Explanation: In cycling, the rear wheel moves by the force communicated to it by pedalling while front wheel moves by it self. So, while pedalling a bicycle, the force exerted by rear wheel on ground makes force of friction act on it in the forward direction (like walking). Front wheel moving by itself experience force of friction in backward direction (like rolling of a ball). [However, if pedalling is stopped both wheels move by themselves and so experience force of friction in backward direction]