1. \(\lim_{x\rightarrow\infty}f(x)^{g(x)}=\lim_{x\rightarrow\infty}f(x)^{\lim_{x\rightarrow\infty}g(x)}\)
a) True
b) False
Explanation: It is a property of limits.
2. \(ln(lim_{x\rightarrow\infty}\frac{f(x)}{g(x)})=\lim_{x\rightarrow\infty}ln(f(x))+\lim_{x\rightarrow\infty}ln(g(x))\)
a) True
b) False
Explanation:
\(ln(lim_{x\rightarrow\infty}\frac{f(x)}{g(x)})=ln(\frac{\lim_{x\rightarrow\infty}f(x)}{\lim_{x\rightarrow\infty}g(x)})\)
\(\Rightarrow ln(\lim_{x\rightarrow\infty}\frac{f(x)}{g(x)}) = \lim_{x\rightarrow\infty}ln(f(x)) – \lim_{x\rightarrow\infty}ln(g(x))\)
3. Evaluate limx → 1[(xx – 1) / (xlog(x))].
a) ee
b) e
c) 1
d) e2
Explanation: limx → 1 [(xx – 1) / (xlog(x))] = (0⁄0)
By L hospital rule,
limx → 1 [xx (1+xlog(x))/ (1+xlog(x))] = limx → 1 [xx] = 1.
4. Find n for which \(\lim_{x\rightarrow 0}\frac{(cos(x)-1)(cos(x)-e^x)}{x^n}\), has non zero value.
a) >=1
b) >=2
c) <=2
d) ~2
Explanation: \(\lim_{x\rightarrow 0}\frac{(cos(x)-1)(cos(x)-e^x)}{x^n}=(0/0)\)
By L’Hospital Rule two times we get
=>\(\lim_{x\rightarrow 0}\frac{sin(2x)+e^x(cos(x)+sin(x))}{n(n-1)x^{n-2}}\)
Hence, limit have non zero limit, if n ≠ 0 and (n-1) ≠ 0 and (n-2) >= 0 means n >= 2.
5. Find the value of limx → 0(Sin(2x))Tan2 (2x)?
a) e0.5
b) e-0.5
c) e-1
d) e
Explanation: y=\(\lim_{x\rightarrow 0}(sin(2x))^{tan^2(2x)}\)
Taking log of both side
\(ln y=\lim_{x\rightarrow 0}\frac{ln(sin(2x))}{cot^2(2x)}(0/0)\)
By L’Hospital Rule
\(ln y=-\lim_{x\rightarrow 0}\frac{2cos(2x)}{sin(2x).4.cosec^2(2x)cot(2x)}=-0.5\lim_{x\rightarrow 0}sin^2(2x)\)=-0.5
=>y=e-0.5
6. Evaluate \(\lim_{x\rightarrow\infty}\left [\frac{x-1}{x-2} \right ]^x\).
a) 1⁄4
b) 1⁄3
c) 1⁄2
d) 1
Explanation: \(y=\lim_{x\rightarrow\infty}\left [\frac{x-1}{x-2} \right ]^x\)
\(ln y=\lim_{x\rightarrow\infty}xln\left [\frac{x-1}{x-2} \right ]\)
=>\(\lim_{x\rightarrow\infty}\frac{\left [\frac{x-1}{x-2} \right ]}{\frac{1}{x}}\)
By putting 1=1/y, we get
=>\(\lim_{y\rightarrow 0}\frac{ln\left [\frac{x-1}{x-2} \right ]}{y}=[ln(1/2)]/0\) (i.e indeterminate)
Hence by applying L’Hospital rule
=>\(\lim_{y\rightarrow 0}\frac{ln\left [\frac{x-1}{x-2} \right ]}{y}=\lim_{y\rightarrow 0}\frac{\frac{2-y-1+y}{(2-y)^2}}{\frac{1-y}{2-y}}=\lim_{y\rightarrow 0}\frac{\frac{1}{2-y}}{\frac{1-y}{1}}=\lim_{y\rightarrow 0}(\frac{1}{(2-y)(1-y)})\)=1/2
7. For the cartesian curve y=f(x) with ‘s’ as arc length which of the following condition holds good?
a) \(\frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\)
b) \(\frac{d^2s}{dx^2} = \sqrt{1-(\frac{dy}{dx})^2}\)
c) \(\frac{dy}{dx} = \sqrt{1+(\frac{ds}{dx})^2}\)
d) \(\sqrt{(\frac{ds}{dx})^2 + (\frac{dy}{dx})^2} = 1\)
Explanation: We can notice that ds is parallel to tangent to the curve, thus ds segment make an angle of φ with x-axis in positive direction
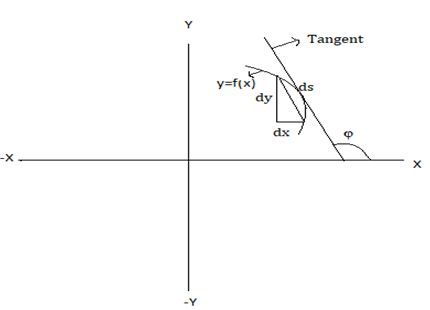
\(\frac{dy}{ds} = sinφ, \frac{dx}{ds} = cosφ, \frac{ds}{dx} = secφ, i.e (\frac{dx}{ds})^2 = sec^2 φ = 1+tan^2 φ…(1)\)
but \(tan φ=\frac{dy}{dx}\) = slope
substituting in (1) we get \( 1+(\frac{dy}{dx})^2 = (\frac{ds}{dx})^2 = \frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\).
8. For the curve \(y=a \,log \,sec(\frac{x}{a})\) what is the value of \( \frac{ds}{dx}\)? (where φ is the angle made by tangent to the curve with x-axis)?
a) cos φ
b) sec φ
c) tan φ
d) cot φ
Explanation: w.k.t \(\frac{ds}{dx} = \sqrt{1+(\frac{dy}{dx})^2}\)
\(\frac{dy}{dx} = a \frac{tan \frac{x}{a}.sec\frac{x}{a}}{sec\frac{x}{a}} \frac{1}{a} = tan \frac{x}{a} \)
substituting we get
\(\frac{ds}{dx} = \sqrt{1+(tan \frac{x}{a})^2}=sec\frac{x}{a}, \,but \,w.k.t\, \frac{dy}{dx} = tan φ = tan\frac{x}{a} \,thus\, φ=\frac{x}{a}\)
\(\frac{ds}{dx} = secφ.\)
9. If the parametric equation of the curve is given by x=aet sint & y=aet cos t the value of \(\frac{ds}{dt}\) is given by _____
a) aet
b) 2aet
c) √3 aet
d) √2 aet
Explanation: w.k.t \(\frac{ds}{dt} = \sqrt{(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2}…(1)\)
\(\frac{dx}{dt} = ae^t (cos t + sin t), \frac{dy}{dt} = ae^t (-sin t + cost)\)
substituting in (1) we get
\(\frac{ds}{dt} = ae^t \sqrt{(cos t + sin t)^2+(-sin t+cost)^2}\)
\(\frac{ds}{dt} = ae^t \sqrt{1+2 sin t cos + 1 – 2 sin t cost} = \sqrt{2} ae^t…(cos^{2} t + sin{2} t = 1).\)
10. For the curve in polar form \(\sqrt{\frac{r}{a}} = sec(\frac{θ}{2}) \,the\, \,value\, \,of\, \frac{ds}{dθ}\) is _____
a) r sec θ
b) r sec \((\frac{θ}{2})\)
c) r sec (2θ)
d) r cosec \((\frac{θ}{2})\)
Explanation: Squaring the given curve on both side i.e \(r=a sec ^2 (\frac{θ}{2})\)…(1)
\(\frac{dr}{dθ} = a.2 sec(\frac{θ}{2}) sec(\frac{θ}{2}) tan (\frac{θ}{2}).1/2 = a sec^2 (\frac{θ}{2}) tan(\frac{θ}{2}) \)
from (1)
\(\frac{dr}{dθ} = r tan (\frac{θ}{2}) \,the\, \,equation\, \,for\, \frac{ds}{dθ} \,is\, = \sqrt{(r^2+(\frac{dr}{dθ})^2)} = \sqrt{r^2(1+ tan^2 (\frac{θ}{2}))} \)
\(\frac{ds}{dθ} = r sec (\frac{θ}{2}).\)