1. A and B can together do a piece of work it in 6 days and A alone can do it in 9 days. The number of days B will take to do it alone is ?
a) 18 days
b) 24 days
c) 9 days
d) 12 days
Explanation:L.C.M. of Total Work = 36
One day work of A + B = $$\frac{{36}}{{6}}$$ = 6 unit/day
One day work of A = $$\frac{{36}}{{9}}$$ = 4 unit/day
$$\eqalign{ & {\text{B's efficiency}} \cr & = 6 - 4 \cr & = 2 \cr & {\text{Time taken by B}} \cr & = \frac{{36}}{2} \cr & = 18{\text{ days}} \cr} $$
2. A can do a piece of work in 18 days. He worked at it for 12 days and B finished the remaining work in 8 days. B alone can do the whole work in ?
a) 16 days
b) 24 days
c) 35 days
d) 28 days
Explanation:
$$\eqalign{ & {\text{18A}} = {\text{12A}} + {\text{8B}} \cr & {\text{6A}} = {\text{8B}} \cr & \frac{{\text{A}}}{{\text{B}}} = \frac{4}{3} \cr & {\text{So, }} \cr & {\text{Efficiency of A and B are }}4,3. \cr & {\text{Total work}} \cr & = 18 \times 4 \cr & = 72{\text{ units}} \cr & {\text{So, B will do}} \cr & = \frac{{72}}{3} \cr & = 24{\text{ days}} \cr} $$
3. A and B can do a work in 8 days, B and C can do the same work in 12 days. A, B and C together can finish it in 6 days. A and C together will do it in ?
a) 4 days
b) 6 days
c) 8 days
d) 12 days
Explanation: L.C.M. of Total Work = 24
One day work of A + B = $$\frac{{24}}{{8}}$$ = 3 unit/day
One day work of B + C = $$\frac{{24}}{{12}}$$ = 2 unit/day
One day work of A + B + C = $$\frac{{24}}{{6}}$$ = 4 unit/day
$$\eqalign{ & {\text{Efficiency of C}} \cr & = 4 - 3 \cr & = 1 \cr & {\text{Efficiency of A}} \cr & = 4 - 2 \cr & = 2 \cr & {\text{Efficiency of B}} \cr & = 4 - 1 \cr & = 3 \cr & {\text{Efficiency of A}} + {\text{C}} \cr & = 2 + 1 \cr & = 1 \cr & {\text{Time taken by A}} + {\text{C}} \cr & = \frac{{24}}{3} \cr & = 8{\text{ days}} \cr} $$
4. A can do a certain job in 12 days and B is 60% more efficient than A. The B can do the same piece of work in ?
a) $${\text{8 days}}$$
b) $${\text{7}}\frac{1}{2}{\text{ days}}$$
c) $${\text{6}}\frac{1}{4}{\text{ days}}$$
d) $${\text{6 days}}$$
Explanation: Ratio of time, taken by A and B = 160 : 100 = 8 : 5
If A takes 8 days, B takes 5 days
If A takes 12 days,
B takes $${\text{ = }}\frac{5}{8} \times 12 = \frac{{15}}{2} = 7\frac{1}{2}$$ days
5. A man can do a piece of work in 30 hours. If he works with his son then the same piece of work is finished in 20 hours. If the son works alone then he do the work in ?
a) 60 hours
b) 50 hours
c) 25 hours
d) 10 hours
Explanation:L.C.M. of Total Work = 60
One hours work of M = $$\frac{{60}}{{30}}$$ = 2 unit/hours
One hours work of M + S = $$\frac{{60}}{{20}}$$ = 3 unit/hours
$$\eqalign{ & {\text{Efficiency of S}} \cr & = 3 - 2 \cr & = 1 \cr & {\text{Required time}} \cr & = \frac{{60}}{1} \cr & {\text{ = }}60{\text{ hours }} \cr} $$
6. A takes 10 days less than the time taken by B to finish a piece of work. If both A and B can do it in 12 days, then the time taken by B alone to finish the work is = ?
a) 30 days
b) 27 days
c) 20 days
d) 25 days
Explanation:Let B can alone finish the work = x days
So, A can alone finish the work = (x - 10) days
Now, one day work of A = $$\frac{1}{{{\text{x}} - 10}}$$
and one day work of B = $$\frac{1}{{\text{x}}}$$
Now, given (A + B) can finish the work = 12 day
So, one day work of (A + B) = $$\frac{1}{{12}}$$
$$\eqalign{ & \Rightarrow \frac{1}{{{\text{x}} - 10}} + \frac{1}{{\text{x}}} = \frac{1}{{12}} \cr & \Rightarrow \frac{{x + x - 10}}{{x \times \left( {x - 10} \right)}} = \frac{1}{{12}} \cr & \Rightarrow \frac{{2x - 10}}{{{x^2} - 10x}} = \frac{1}{{12}} \cr & \Rightarrow 12\left( {2x - 10} \right) = {x^2} - 10x \cr & \Rightarrow 24x - 120 = {x^2} - 10x \cr & \Rightarrow {x^2} - 10x - 24x + 120 = 0 \cr & \Rightarrow {x^2} - 34x + 120 = 0 \cr & \Rightarrow {x^2} - 30x - 4x + 120 = 0 \cr & \Rightarrow x\left( {x - 30} \right) - 4\left( {x - 30} \right) = 0 \cr & \Rightarrow \left( {x - 30} \right) \times \left( {x - 4} \right) = 0 \cr & \Rightarrow x = 30,\,4 \cr} $$
if x = 4, then A alone can finish the work = 4 - 10 = -6, which is not possible.
So, x = 30
Hence, B can alone finish the work = 30 days
7. Dinesh and Rakesh are working on an Assignment, Dinesh takes 6 hours to type 32 pages on a computer, while Rakesh takes 5 hours to type 40 pages. How much time will they take working together on two different computers to type an assignment of 110 page ?
a) 7 hours, 30 minutes
b) 8 hours
c) 8 hours, 15 minutes
d) 8 hours, 25 minutes
Explanation:
$$\eqalign{ & {\text{Dinesh's one hour work}} \cr & = \frac{{32}}{6} \cr & = \frac{{16}}{3}{\text{ pages/hour}} \cr & {\text{Rakesh's one hour work}} \cr & = \frac{{40}}{5} \cr & = 8{\text{ pages/hour}} \cr & {\text{Dinesh's and Rakesh's one hour work}} \cr & = \frac{{16}}{3} + 8 \cr & = \frac{{40}}{3}{\text{ pages/hour}} \cr & {\text{They will finish the work together}} \cr & \frac{{{\text{Total work}}}}{{{\text{Efficiency}}}} \cr & = \frac{{110}}{{\frac{{40}}{3}}} \cr & = 8\frac{1}{4} \cr & = {\text{8 hours, 15 minutes}} \cr} $$
8. A can do as much work as B and C together can do. A and B can together do a piece of work in 9 hours 36 minutes and C can do it in 48 hours. The time in hours that B needs to do the work alone, is ?
a) 18 hours
b) 24 hours
c) 30 hours
d) 12 hours
Explanation: 9 hours 36 minutes
$$\eqalign{ & = 9 + \frac{{36}}{{60}}\,{\text{hours}} \cr & = 9\frac{3}{5} = \frac{{48}}{5}{\text{hours}} \cr} $$
(A + B)’s 1 hour’s work = $$\frac{5}{{48}}$$
C’s 1 hour’s work = $$\frac{1}{{48}}$$
(A + B + C)’s 1 hour’s work = $$\frac{5}{{48}} + \frac{1}{{48}}$$ = $$\frac{1}{8}$$ . . . . . . .(i)
A’s 1 hour’s work = (B + C)’s 1 hour’s work . . . . . . . . (ii)
From equation (i) and (ii),
2 × (A’s 1 hour’s work) = $$\frac{1}{8}$$
A’s 1 hour’s work = $$\frac{1}{{16}}$$
∴ B’s 1 hour’s work
$$\eqalign{ & = \frac{5}{{48}} - \frac{1}{{16}} \cr & = \frac{{5 - 3}}{{48}} \cr & = \frac{1}{{24}} \cr} $$
∴ B alone will finish the work in 24 hours.
9. If 5 men and 3 women can reap 18 acre of crop in 4 days, 3 men and 2 women can reap 22 acre of crop in 8 days, then how many men are required to join 21 women to reap 54 acre of crop in 6 days ?
a) 5
b) 6
c) 10
d) 12
Explanation: Acreage reaped by 5 men and 3 women in 1 day
$$\eqalign{ & = \frac{{18}}{4} \cr & = \frac{9}{2} \cr} $$
Acreage reaped by 3 men and 2 women in 1 day
$$\eqalign{ & = \frac{{22}}{8} \cr & = \frac{{11}}{4} \cr} $$
Suppose 1 man can reap x acres in 1 day and 1 women can reap y acres in 1 day
$$\eqalign{ & \therefore 5x + 3y = \frac{9}{2} \cr & \Rightarrow 10x + 6y = 9\,.....{\text{(i)}} \cr & 3x + 2y = \frac{{11}}{4} \cr & \Rightarrow 9x + 6y = \frac{{33}}{4}\,.....{\text{(ii)}} \cr & {\text{Subtracting (ii) from (i),}} \cr & {\text{We get}}:x = 9 - \frac{{33}}{4} = \frac{3}{4} \cr & {\text{Putting x}} = \frac{3}{4}{\text{ in (i), we get}} \cr & \Rightarrow 6y = 9 - \frac{{15}}{2} \cr & \Rightarrow 6y = \frac{3}{2} \cr & \Rightarrow y = \frac{1}{4} \cr} $$
Acreage reaped by 21 women in 6 days
$$\eqalign{ & = \left( {\frac{1}{4} \times 21 \times 6} \right) \cr & = \frac{{63}}{2} \cr} $$
Remaining acreage to be reaped
$$\eqalign{ & = \left( {54 - \frac{{63}}{2}} \right) \cr & = \frac{{45}}{2} \cr} $$
Acreage reaped by 1 men in 6 days
$$\eqalign{ & = \left( {\frac{3}{4} \times 6} \right) \cr & = \frac{9}{2} \cr} $$
In 6 days, $$\frac{9}{2}$$ acre is reaped by 1 man
∴ In 6 days, $$\frac{{45}}{2}$$ acre is reaped by
$$\eqalign{ & = \left( {\frac{2}{9} \times \frac{{45}}{2}} \right){\text{men}} \cr & = 5{\text{ men}} \cr} $$
10. 25 men with 10 boys can do in 6 days as much work as 21 men with 30 boys can do in days. How many boys must help 40 men to do the same work in 4 days ?
a) 5
b) 10
c) 20
d) 40
Explanation:
$$\eqalign{ & {\text{Let 1 men's 1 day's work}} = x \cr & {\text{and 1 boy's 1 day's work}} = y \cr & {\text{Then, }} \cr & \Rightarrow {\text{6}}\left( {25x + 10y} \right) = 5\left( {21x + 30y} \right) \cr & \Rightarrow 150x + 60y = 105x + 150y \cr & \Rightarrow 45x = 90y \cr & \Rightarrow x = 2y \cr & {\text{Let,}} \cr & {\text{The required number of boys be }}z \cr & {\text{Then,}} \cr & \Rightarrow {\text{4}}\left( {40x + zy} \right) = 6\left( {25x + 10y} \right) \cr & \Rightarrow 4\left( {80y + zy} \right) = 6\left( {50y + 10y} \right) \cr & \Rightarrow 80 + z = \frac{{6 \times 60}}{4} = 90 \cr & \Rightarrow z = 10 \cr} $$
11. If 2 men or 6 women or 4 boys can finish a work in 99 days, how many days will one man, one woman and one boy together take to finish the same work ?
a) 44 days
b) 54 days
c) 64 days
d) None of these
Explanation:
$$\eqalign{ & {\text{1 men's 1 day's work}} \cr & = \frac{1}{{99 \times 2}} \cr & = \frac{1}{{198}} \cr & {\text{1 women's 1 day's work}} \cr & = \frac{1}{{99 \times 6}}. \cr & = \frac{1}{{594}} \cr & {\text{1 boy's 1 day's work}} \cr & = \frac{1}{{99 \times 4}} \cr & = \frac{1}{{396}} \cr} $$
(1 men + 1 women + boy)'s 1 day's work
$$\eqalign{ & = \frac{1}{{198}} + \frac{1}{{594}} + \frac{1}{{396}} \cr & = \frac{{11}}{{1188}} \cr & = \frac{1}{{108}} \cr} $$
Hence, 1 mens , 1 women and 1 boys together take 108 days to finish the work
12. 8 men can complete a piece of work in 20 days. 8 women can complete the same work in 32 days. In how many days will 5 men and 8 women together complete the same work ?
a) 10 days
b) 12 days
c) 14 days
d) 16 days
Explanation:
$$\eqalign{ & {\text{1 men's 1 day's work}} \cr & = \frac{1}{{20 \times 8}} \cr & = \frac{1}{{160}} \cr & {\text{1 women's 1 day's work}} \cr & = \frac{1}{{32 \times 8}} \cr & = \frac{1}{{256}} \cr & \left( {{\text{5 men}} + {\text{8 women}}} \right){\text{'s 1 day's work}} \cr & = \frac{5}{{160}} + \frac{8}{{256}} \cr & = \frac{1}{{32}} + \frac{1}{{32}} \cr & = \frac{1}{{16}} \cr} $$
Hence, 5 mens and 8 women together can complete the work in 16 days
13. A can do three times the work done by B in one day. They together finish $$\frac{2}{5}$$ of the work in 9 days. The number of days by which B can do the work alone are ?
a) 120 days
b) 100 days
c) 30 days
d) 90 days
Explanation: Efficiency of A = 3 efficiency of B
$$\left( {{\text{A}} = 3,{\text{B}} = 1} \right)$$
$$\frac{2}{5}$$ th of the work done by (A + B) in 9 days
Total work (A + B) = $$\frac{{45}}{2}$$ days will be completed
$$\eqalign{ & {\text{Total work}} \cr & = {\text{days}} \times {\text{efficiency }}\left( {{\text{A}} + {\text{B}}} \right) \cr & = \frac{{45}}{2} \times 4 \cr & = 90 \cr & {\text{Number of days for B }} \cr & {\text{ = }}\frac{{{\text{Total work}}}}{{{\text{Efficiency}}}} \cr & = \frac{{90}}{1} \cr & = 90{\text{ days}} \cr} $$
14. A can write 75 pages in 25 hours. A and B together can write 135 pages in 27 hours. In what time can B write 42 pages ?
a) 17 hrs
b) 19 hrs
c) 21 hrs
d) 23 hrs
Explanation:
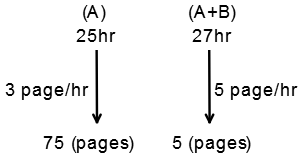
B's efficiency
= (A + B)'s efficiency - A's efficiency
= 5 - 3
= 2 pages/hour
B's time
2 pages in 1 hour
42 pages in 21 hours
15. A and B can complete a piece of work in 12 and 18 days respectively. A begins to do the work and they work alternatively one at a time for one day each. The whole work will be complete in ?
a) $${\text{14}}\frac{1}{3}{\text{ days}}$$
b) $${\text{15}}\frac{1}{3}{\text{ days}}$$
c) $${\text{16}}\frac{1}{3}{\text{ days}}$$
d) $${\text{18}}\frac{2}{3}{\text{ days}}$$
Explanation: A's one day work = 3 units
B's one day work = 2 units
A starts the work and does 3 units and B does the work 2 units/day.
They both do 5 units of work in 2 days.
They both do 35 units of work in 14 days
(Divide $${\frac{{36}}{5}}$$, take it to the closest)
$$\eqalign{ & {\text{Work left }} \Rightarrow 36 - 35 = 1{\text{unit}}{\text{.}} \cr & {\text{Now, A's turn}}{\text{.}} \cr & {\text{A completes}} \cr & \Rightarrow \frac{{1{\text{ unit}}}}{{{\text{3 units/day}}}} \cr & = \frac{1}{3}{\text{ day}} \cr & {\text{Whole work completes in}} \cr & \Rightarrow 14 + \frac{1}{3} \cr & = 14\frac{1}{3}{\text{ days}} \cr} $$
16. 40 men can complete a piece of work in 15 days. 20 more men joined them after 5 days they start doing work. How many days will be required by them to finish the remaining work ?
a) $${\text{7}}\frac{2}{3}{\text{ days}}$$
b) $${\text{6}}\frac{1}{5}{\text{ days}}$$
c) $${\text{8}}\frac{1}{4}{\text{ days}}$$
d) $${\text{6}}\frac{2}{3}{\text{ days}}$$
Explanation: Work done by 40 men in 5 days = $$\frac{1}{3}$$
(As if whole work is completed in 15 days then in 5 days $${{{\frac{1}{3}}^{{\text{rd}}}}}$$ of the work will be finished)
$$\eqalign{ & {\text{Remaining work}} = 1 - \frac{1}{3} = \frac{2}{3} \cr & \because 40{\text{ men do 1 work in 15 days}}{\text{.}} \cr & {\text{60 men can do }}\frac{2}{3}{\text{work in }}x{\text{ day}} \cr & \frac{{{{\text{M}}_1}{{\text{D}}_1}}}{{{{\text{W}}_1}}}{\text{ = }}\frac{{{{\text{M}}_2}{{\text{D}}_2}}}{{{{\text{W}}_2}}} \cr & {{\text{M}}_1} = 40{\text{ , }}{{\text{M}}_2} = 60 \cr & {{\text{D}}_1} = 15{\text{ , }}{{\text{D}}_2} = x \cr & {{\text{W}}_1} = 1{\text{ ,}}{{\text{W}}_2} = \frac{2}{3} \cr & \Rightarrow \frac{{40 \times 15}}{1} = \frac{{60 \times x}}{2} \cr & \Rightarrow \frac{2}{3}\left( {40 \times 15} \right) = 60x \cr & \Rightarrow 2 \times 40 \times 5 = 60x \cr & \Rightarrow x = \frac{{20}}{3} \cr & \Rightarrow x = 6\frac{2}{3}{\text{ days}} \cr} $$
17. A and B working separately can do a piece of work in 9 and 15 days respectively. If they work for a day alternatively, with A beginning, then the work will be completed in ?
a) 10 days
b) 11 days
c) 9 days
d) 12 days
Explanation: L.C.M. of Total Work = 45
One day work of A = $$\frac{{45}}{{9}}$$ = 5 unit/day
One day work of B = $$\frac{{45}}{{15}}$$ = 3 unit/day
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 2 days work }} \cr & = 5 + 3 \cr & = 8{\text{ units}} \cr & {\text{They will do in }} \cr & = \frac{{40}}{8} \times 2 \cr & = \left( {5 \times 2} \right) \cr & = 10{\text{ days}} \cr & \therefore {\text{Work left}} \cr & = 45 - 40 \cr & = {\text{5 units}} \cr & {\text{Now,}} \cr & {\text{A's turn and he will complete in}} \cr & = \frac{5}{5} \cr & = 1{\text{ days}} \cr & {\text{Then total work completed in}} \cr & = 10 + 1 \cr & = 11{\text{ days}} \cr} $$
18. 12 monkeys can eat 12 bananas in 12 minutes. In how many minutes can 4 monkeys eat 4 bananas ?
a) 4 minutes
b) 10 minutes
c) 12 minutes
d) 8 minutes
Explanation:
$$\eqalign{ & {\text{Let the required time}} = {\text{T}} \cr & \Rightarrow \frac{{{{\text{m}}_{\text{1}}} \times {{\text{d}}_{\text{1}}} \times {{\text{t}}_{\text{1}}}}}{{{{\text{w}}_{\text{1}}}}}{\text{ = }}\frac{{{{\text{m}}_{\text{2}}} \times {{\text{d}}_{\text{2}}} \times {{\text{t}}_{\text{2}}}}}{{{{\text{w}}_{\text{2}}}}} \cr & \Rightarrow \frac{{12 \times 12}}{{12}} = \frac{{4 \times {\text{time}}}}{4} \cr & \Rightarrow {\text{Time}} = 12\operatorname{minutes} \cr} $$
19. Two worker A and B are engaged to do a piece of work. A working alone would take 8 hours more to complete the work that when work together. If B worked alone, would take $${\text{4}}\frac{1}{2}$$ hours more than when working together. The time required to finish the work together is = ?
a) 5 hours
b) 8 hours
c) 4 hours
d) 6 hours
Explanation:
$$\eqalign{ & {\text{Let,}} \cr & {\text{a}} = {\text{8h}} \cr & {\text{b}} = {\text{4}}\frac{1}{2}{\text{h}} = \frac{9}{2}{\text{h}} \cr} $$
Time required to finish the work together
$$\eqalign{ & = \sqrt {{\text{ab}}} \cr & = \sqrt {8 \times \frac{9}{2}} \cr & = 6{\text{ h}} \cr} $$
20. X can copy 80 pages in 20 hours, x and y together can copy 135 pages in 27 hours. Then y can copy 20 pages in ?
a) 20 hours
b) 24 hours
c) 3 hours
d) 12 hours
Explanation:
$$\eqalign{ & \Rightarrow {{\text{R}}_{\text{x}}} \cr & = \frac{{80}}{{20}} \cr & {\text{ = 4 pages/hour}} \cr & \Rightarrow {{\text{R}}_{{\text{x + y}}}} \cr & = \frac{{135}}{{27}} \cr & {\text{ = 5 pages/hour}} \cr & \Rightarrow {{\text{R}}_{\text{y}}} \cr & = {{\text{R}}_{{\text{x + y}}}} - {{\text{R}}_{\text{x}}} \cr & = 5 - 4 \cr & = 1{\text{ pages/hour}} \cr & \therefore {\text{y can copy 20 pages in}} \cr & = \frac{{{\text{20p}}}}{{{\text{1p/h}}}} \cr & = {\text{ }}20{\text{ hours}} \cr} $$
21. Amit, Bhawana and Chandan can do a piece of work, working together in one day only. Amit is 5 times efficient than Bhawna and Chandan takes half of the number of days taken by Bhawna to do the same work. What is the difference between the number of days taken by Amit and Chandan when they work alone ?
a) 4
b) 5
c) 3
d) $${\text{2}}\frac{2}{5}$$
Explanation:
| Amit | Bhawana | Chandan | |
| Eff. → | 5x | x | 2x |
$$\eqalign{ & {\text{Let total work}} = 1 \cr & {\text{Efficiency of }}\left( {{\text{A}} + {\text{B}} + {\text{C}}} \right) = 1 \cr & {\text{Then,}} \cr & \Leftrightarrow 5x + x + 2x = 1 \cr & \Leftrightarrow x = \frac{1}{8} \cr & {\text{Days taken by Amit}} \cr & = \frac{1}{{\frac{5}{8}}} \Rightarrow \frac{8}{5} \cr & {\text{Days taken by Chandan}} \cr & = \frac{1}{{\frac{2}{8}}} \Rightarrow 4 \cr & {\text{Difference of days}} \cr & = 4 - \frac{8}{5} \Rightarrow \frac{{20 - 8}}{5} \Rightarrow 2\frac{2}{5} \cr} $$
22. 12 men can do a piece of work in 15 days and 20 women can do the same work in 12 days. In how many days can 5 men and 5 women complete the same work ?
a) $${\text{20}}\frac{4}{7}{\text{ days}}$$
b) $${\text{2}}\frac{4}{7}{\text{ days}}$$
c) $${\text{20}}\frac{3}{7}{\text{ days}}$$
d) 18 days
Explanation: 12 man × 15 = 20 women × 12 = Total work
3 man = 4 women
$$\eqalign{ & \frac{{{\text{Men}}}}{{{\text{Women}}}} = \frac{4}{3} \to {\text{Efficiency}} \cr & {\text{Total work}} = 12 \times 4 \times 15 = 720 \cr & \left( {5{\text{ man}} + 5{\text{ women}}} \right) \times {\text{D}} = 720 \cr & {\text{D}}\left( {5 \times 4 + 5 \times 3} \right) = 720 \cr & {\text{D}} = \frac{{720}}{{35}} = 20\frac{4}{7}{\text{ days}} \cr} $$
23. X can do a piece of work in 24 days. When he had worked for 4 days, Y joined him. If complete work was finished in 16 days, Y can alone finish that work in ?
a) 18 days
b) 27 days
c) 36 days
d) 42 days
Explanation:
$$\eqalign{ & {\text{X's 1 day's work}} = \frac{1}{{24}} \cr & {\text{X's 16 day's work}} = \frac{{16}}{{24}} \cr & {\text{Let,}} \cr} $$
Y alone complete the work in x days
$${\text{Y's 12 day's work}} = \frac{{12}}{x}$$
According to the question,
Complete work done by X and Y = 1
X's 16 day's work + Y's 12 day's work = 1
$$\eqalign{ & \Rightarrow \frac{{16}}{{24}} + \frac{{12}}{x} = 1 \cr & \Rightarrow \frac{2}{3} + \frac{{12}}{x} = 1 \cr & \Rightarrow \frac{{12}}{x} = 1 - \frac{2}{3} = \frac{1}{3} \cr & \Rightarrow x = 12 \times 3 \cr & \Rightarrow x = 36{\text{ days}} \cr} $$
24. 6 men can complete a piece of work in 12 days, 8 women can complete the same piece of work in 18 days and 18 children can do it in 10 days. 4 men, 12 women and 20 children do the work for 2 days. If the remaining work be completed by men only in 1 day, how many men will be required ?
a) 36
b) 24
c) 18
d) Cannot be determined
Explanation: 6 men will complete the work in 12 days
1 men will complete the work in (6 × 12) = 72 days
8 women will complete two work in 18 days
1 women will complete the work in (8 × 18) = 144 days
18 children will complete the work in 10 days
1 children will complete the work in (18 × 10) = 180 days
$$\eqalign{ & {\text{1 men's 1 day's work}} = \frac{1}{{72}} \cr & {\text{1 women's 1 day's work}} = \frac{1}{{144}} \cr & {\text{1 children's 1 day's work}} = \frac{1}{{180}} \cr} $$
(4 men + 12 women + 20 children)'s 2 day's work
$$\eqalign{ & = 2\left( {\frac{4}{{72}} + \frac{{12}}{{144}} + \frac{{20}}{{180}}} \right) \cr & = 2\left( {\frac{1}{{18}} + \frac{1}{{12}} + \frac{1}{9}} \right) \cr & {\text{L}}{\text{.C}}{\text{.M of 18, 12 and 9}} = {\text{36}} \cr & {\text{ = }}\frac{{2\left( {2 + 3 + 4} \right)}}{{36}} \cr & = \frac{1}{2} \cr & \therefore {\text{Remaining work}} = \frac{1}{2} \cr & \therefore {\text{Required number of men}} \cr & = 72 \times \frac{1}{2} \cr & = 36 \cr} $$
25. 16 men can finish a piece of work in 49 days. 14 men started working and 8 days they could finish certain amount of work. If it is required to finish the remaining work in 24 days. How many more men should be added to the existing workforce ?
a) 21
b) 28
c) 16
d) 14
Explanation:
$$\eqalign{ & {\text{Given,}} \cr & {{\text{M}}_1} = 16{\text{ , }}{{\text{M}}_2} = ? \cr & {{\text{D}}_1} = 49{\text{ , }}{{\text{D}}_2} = 24 \cr & {{\text{W}}_1} = 1{\text{ ,}}{{\text{W}}_2} = ? \cr & {\text{According to the question,}} \cr & \frac{{{{\text{M}}_1}{{\text{D}}_1}}}{{{{\text{W}}_1}}}{\text{ = }}\frac{{{{\text{M}}_2}{{\text{D}}_2}}}{{{{\text{W}}_2}}} \cr & \Rightarrow \frac{{16 \times 49}}{1} = \frac{{14 \times 8}}{{{{\text{W}}_2}}} \cr & \Rightarrow {{\text{W}}_2} = \frac{{14 \times 8}}{{16 \times 49}} \cr & \Rightarrow {{\text{W}}_2} = \frac{1}{7} \cr & {\text{Remaining work}} \cr & = \left( {1 - \frac{1}{7}} \right) \cr & = \frac{6}{7} \cr & {\text{Again,}}\frac{{{{\text{M}}_1}{{\text{D}}_1}}}{{{{\text{W}}_1}}}{\text{ = }}\frac{{{{\text{M}}_2}{{\text{D}}_2}}}{{{{\text{W}}_2}}} \cr & \Rightarrow \frac{{16 \times 49}}{1} = \frac{{{{\text{M}}_2} \times 24}}{{\frac{6}{7}}} \cr & \Rightarrow 16 \times 49 = \frac{{{{\text{M}}_2} \times 24 \times 7}}{6} \cr & \Rightarrow 16 \times 49 = {{\text{M}}_2} \times 4 \times 7 \cr & \Rightarrow {{\text{M}}_2} = \frac{{16 \times 49}}{{4 \times 7}} \cr & \Rightarrow {{\text{M}}_2} = 28 \cr & \therefore {\text{Number of additional men}} \cr & = \left( {28 - 14} \right) \cr & = 14 \cr} $$
26. 12 men can do a piece of work in 24 days. How many days are needed to complete the work, if 8 men do this work ?
a) 28 days days
b) 36 days
c) 48 days
d) 52 days
Explanation: 12 men can do a piece of work in 24 days
$$ \Rightarrow {{\text{M}}_1} = 12{\text{ and }}{{\text{D}}_1} = 24$$
8 men can do this work in $${{\text{D}}_2}$$ days
$$\eqalign{ & \Rightarrow {{\text{M}}_2} = 8{\text{ }} \cr & \,\,\,\,\,\,\,\,\,{{\text{M}}_1}{{\text{D}}_1} = {{\text{M}}_{\text{2}}}{{\text{D}}_{\text{2}}} \cr & \Rightarrow 12 \times 24 = 8 \times {{\text{D}}_2} \cr & \Rightarrow {{\text{D}}_2} = \frac{{12 \times 24}}{8} \cr & \Rightarrow {{\text{D}}_2} = 36{\text{ days}} \cr} $$
27. A can do in one day three times the work done by B in one day. They together finish $$\frac{2}{5}$$ of the work in 9 days. The number of days by which B can do the work alone is = ?
a) 90 days
b) 120 days
c) 100 days
d) 30 days
Explanation: Let time taken by A alone in doing work be x days
∴ Time taken by B alone = 3x days
$$\eqalign{ & {\text{A's 1 day's work}} = \frac{1}{x} \cr & {\text{B's 1 days work}} = \frac{1}{{3x}} \cr & \because {\text{A and B together finish}} \cr & = \frac{2}{5}{\text{work in 9 days}}{\text{.}} \cr} $$
∴ Time taken by A and B in doing whole work
$$\eqalign{ & = \frac{{9 \times 5}}{2} \cr & = \frac{{45}}{2}{\text{ days}} \cr} $$
According to given information we get
$$\eqalign{ & \therefore \frac{1}{x} + \frac{1}{{3x}} = \frac{2}{{45}} \cr & \Rightarrow \frac{{3 + 1}}{{3x}} = \frac{2}{{45}} \cr & \Rightarrow \frac{4}{{3x}} = \frac{2}{{45}} \cr & {\text{By cross - multiply we get }} \cr & \Rightarrow 2 \times 3x = 4 \times 45 \cr & \Rightarrow x = \frac{{4 \times 45}}{{2 \times 3}} \cr & \Rightarrow x = 30{\text{ days}} \cr & {\text{Time taken by A}} \cr & = x{\text{ days}} \cr & = {\text{30 days}} \cr & \therefore {\text{Time taken by B}} \cr & = 3x{\text{ days}} \cr & = 3 \times 30 \cr & = 90{\text{ days}} \cr} $$
28. A, B and C can complete a piece of work in 24, 5 and 12 days respectively. Working together, they will complete the same work in ?
a) $$\frac{7}{{24}}{\text{days}}$$
b) $${\text{3}}\frac{3}{7}{\text{days}}$$
c) $${\text{4 days}}$$
d) $${\text{3}}\frac{1}{{13}}{\text{days}}$$
Explanation:
$$\eqalign{ & {\text{A's 1 day's work}} = \frac{1}{{24}} \cr & {\text{B's 1 day's work}} = \frac{1}{5} \cr & {\text{C's 1 day's work}} = \frac{1}{{12}} \cr & \therefore \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \frac{1}{{24}} + \frac{1}{5} + \frac{1}{{12}} \cr & {\text{L}}{\text{.C}}{\text{.M of 24, 5 and 12}} \cr} $$
| 2 | 24 - 5 - 12 |
| 2 | 12 - 5 - 6 |
| 3 | 6 - 5 - 3 |
| 2 - 5 - 1 |
Time taken by A, B and C to complete the work, working together
$$\eqalign{ & = \frac{{40}}{{13}} \cr & = 3\frac{1}{{13}}{\text{days}} \cr} $$
29. If 4 men and 6 women can complete a work in 8 days, while 3 men and 7 women can complete it in 10 days, then 10 women complete it in ?
a) 35 days
b) 50 days
c) 45 days
d) 40 days
Explanation:
$$\eqalign{ & {\text{According to the question,}} \cr & \Rightarrow {\text{4m}} + {\text{6w}} = 8{\text{ days}}.....{\text{(i)}} \cr & {\text{or}} \cr & \Rightarrow {\text{32m}} + 48{\text{w}} = 1{\text{ days}} \cr & \Rightarrow {\text{3m}} + 7{\text{w}} = 10{\text{ days}}.....{\text{(ii)}} \cr & {\text{or}} \cr & \Rightarrow {\text{30m}} + 70{\text{w}} = 1{\text{ day}} \cr & \therefore {\text{32m}} + {\text{48w}} = 30{\text{m}} + 70{\text{w}} \cr & \Rightarrow {\text{2m}} = 22{\text{w}} \cr & \Rightarrow {\text{m}} = 11{\text{w}} \cr & {\text{From (i)}} \cr & \Rightarrow {\text{4m}} = 44{\text{w}} \cr & \therefore \left( {{\text{44w}} + {\text{6w}}} \right) \times 8 = 10{\text{w}} \times x \cr & \Rightarrow {\text{50w}} \times 8 = 10{\text{w}} \times x \cr & \Rightarrow x = 40{\text{ days}} \cr} $$
30. A can do a piece of work in 12 days and B in 24 days. If they work together, in how many days will they finish the work ?
a) 20 days
b) 8 days
c) 12 days
d) 15 days
Explanation:
| Days | Eff. | Total work |
| A - 12 | 2 | |
| 24 | ||
| B - 12 | 1 | |
| 3 | ||
A and B together can finish the work
$$\eqalign{ & = \frac{{24}}{3} \cr & = 8{\text{ days}} \cr} $$
31. A labourer was appointed by a contractor on the condition he would be paid Rs. 75 for each day of his work but would be, fined at the rate of Rs. 15 per day for his absent. After 20 days, the contractor paid the labourer Rs. 1140. The number of days the labourer absented from work was ?
a) 3 days
b) 5 days
c) 4 days
d) 2 days
Explanation: 4 days
32. 18 men can complete a piece of work in 63 days. 9 women take 189 days to complete the same piece of work. How many days will 4 men, 9 women and 12 children together take to complete the piece of work if 7 children alone can complete the piece of work in 486 days ?
a) 54 days
b) 63 days
c) 76 days
d) 81 days
Explanation:
$$\eqalign{ & {\text{1 men's 1 day's work}} \cr & = \frac{1}{{63 \times 18}} \cr & = \frac{1}{{1134}} \cr & {\text{1 women's 1 day's work}} \cr & = \frac{1}{{189 \times 9}} \cr & = \frac{1}{{1701}} \cr & {\text{1 children's 1 day's work}} \cr & = \frac{1}{{486 \times 7}} \cr & = \frac{1}{{3402}} \cr} $$
(4 men + 9 women + 12 children)'s 1 day's work
$$\eqalign{ & = \frac{4}{{1134}} + \frac{9}{{1701}} + \frac{{12}}{{3402}} \cr & = \frac{{42}}{{3402}} \cr & = \frac{1}{{81}} \cr} $$
Hence, 4 mens , 9 women and 12 children together will complete the work in 81 days.
33. 16 men can finish a work in 24 days and 48 boys can finish the same work in 16 days. 12 men started the work and after 4 days 12 boys joined them. In how many days can they finish the remaining work ?
a) 6
b) 12
c) 16
d) None of these
Explanation:
$$\eqalign{ & {\text{1 men's 1 day's work}} \cr & = \frac{1}{{24 \times 16}} \cr & = \frac{1}{{384}} \cr & {\text{1 boy's 1 day's work}} \cr & = \frac{1}{{16 \times 48}} \cr & = \frac{1}{{768}} \cr & {\text{12 men's 4 day's work}} \cr & = \left( {\frac{{12}}{{384}} \times 4} \right) \cr & = \frac{1}{8} \cr & {\text{Remaining work}} \cr & = \left( {1 - \frac{1}{8}} \right) \cr & = \frac{7}{8} \cr & \left( {{\text{12 men}} + {\text{12 boy}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{{12}}{{384}} + \frac{{12}}{{768}}} \right) \cr & = \left( {\frac{1}{{32}} + \frac{1}{{64}}} \right) \cr & = \frac{3}{{64}} \cr} $$
$$\frac{3}{{64}}$$ work is done by (12 men + 12 boy)'s in 1 day
$$\eqalign{ & \therefore \frac{7}{8}{\text{ work is done by them in }} \cr & {\text{ = }}\frac{{64}}{3} \times \frac{7}{8}{\text{ days}} \cr & = \frac{{56}}{3}{\text{ days}} \cr & = {\text{18}}\frac{2}{3}{\text{ days}} \cr} $$
34. 4 men and 10 women were put on a work. They completed $$\frac{1}{3}$$ of the work in 4 days. After this 2 men and 2 women were increased. They completed $$\frac{2}{9}$$ more of the work in 2 days. If the remaining work is to be completed in 3 days, then how many more women must be increased ?
a) 8
b) 32
c) 55
d) 50
Explanation:
$$\eqalign{ & {\text{Let 1 man's 1 day's work}} = x \cr & {\text{And }} \cr & {\text{1 women's 1 day's work}} = y \cr & {\text{Then,}} \cr & \Rightarrow 4x + 10y = \frac{1}{3} \times \frac{1}{4} = \frac{1}{{12}} \cr & \Rightarrow 4x + 10y = \frac{1}{{12}} \cr & \Rightarrow 2x + 5y = \frac{1}{{24}}.....(i) \cr & {\text{And,}} \cr & \Rightarrow 6x + 12y = \frac{1}{9} \cr & \Rightarrow 2x + 4y = \frac{1}{{27}}.....({\text{ii}}) \cr} $$
Subtracting (ii) from (i), we get
$$\eqalign{ & y = \frac{1}{{24}} - \frac{1}{{27}} = \frac{1}{{216}} \cr & {\text{Now,}} \cr} $$
Now,
(6 men + 12 women)'s 3 day's work
$$\eqalign{ & = \left( {\frac{1}{9} \times 3} \right) \cr & = \frac{1}{3} \cr & {\text{Work completed}} \cr & = \left( {\frac{1}{3} + \frac{2}{9} + \frac{1}{3}} \right) \cr & = \frac{8}{9} \cr & \therefore {\text{Remainig work}} \cr & = \left( {1 - \frac{8}{9}} \right) \cr & = \frac{1}{9} \cr & {\text{1 women's 3 day's work}} \cr & = \left( {\frac{1}{{216}} \times 3} \right) \cr & = \frac{1}{{72}} \cr} $$
In 3 day's $$\frac{1}{{72}}$$ work is done by 1 women.
$$\eqalign{ & \therefore {\text{In 3 day's }}\frac{1}{9}{\text{work is done by}} \cr & {\text{ = }}\left( {72 \times \frac{1}{9}} \right) \cr & = {\text{8 women}}{\text{.}} \cr} $$
35. A can do a piece of work in 5 days less than the time taken by B to do it. If both of them together take $${\text{11}}\frac{1}{9}$$ days, then the time taken by B alone to do the same work (in days ) is ?
a) 15 days
b) 20 days
c) 25 days
d) 30 days
Explanation: Try these question with the help of the option to save the time
Let B takes x days to complete the work
∴ A takes (x - 5)days
Now take the option 'B' i.e x = 20days
∴ Time taken by B = 20days and A = 15days
T.W = LCM of number of day taken by A and B = 60.
Work Efficiency ration A : B = 4 : 3
∴Total Time taken to complete the work together = $$\frac{60}{4+3}$$ = $$8\frac{4}{7}$$ days
This option not matched with $${\text{11}}\frac{1}{9}$$
Now take the option 'C' i.e x = 25days
∴ Time taken by B = 25days and A = 20days
T.W = LCM of number of day taken by A and B = 100.
Work Efficiency ration A : B = 5 : 4
∴Total Time taken to complete the work together = $$\frac{100}{5+4}$$ = $$11\frac{1}{9}$$ days
Hence , Option (C) is the correct .
36. A and B can complete a piece of work in 12 and 18 days respectively. A begins to do the work and they work alternatively one at a time for one day each. The whole work will be completed in ?
a) $${\text{14}}\frac{1}{3}{\text{ days}}$$
b) $${\text{15}}\frac{2}{3}{\text{ days}}$$
c) $${\text{16}}\frac{1}{3}{\text{ days}}$$
d) $${\text{18}}\frac{2}{3}{\text{ days}}$$
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 2 days work}} \cr & = \left( {\frac{1}{{12}} + \frac{1}{{18}}} \right) \cr & = \frac{5}{{36}} \cr & {\text{Work done in 7 pairs of days}} \cr & = \left( {\frac{5}{{36}} \times 7} \right) \cr & = \frac{{35}}{{36}} \cr & {\text{Remaining work}} \cr & = \left( {1 - \frac{{35}}{{36}}} \right) \cr & = \frac{1}{{36}} \cr & {\text{On 15th day, it is A's turn}}{\text{.}} \cr & \frac{1}{{12}}{\text{ work is done by A in 1 day}}{\text{.}} \cr & \frac{1}{{36}}{\text{ work is done by A in}} \cr & = \left( {12 \times \frac{1}{{36}}} \right) \cr & = \frac{1}{3}{\text{ day}}{\text{.}} \cr & \therefore {\text{Total time taken}} = 14\frac{1}{3}{\text{ days}} \cr} $$
37. A can do a piece of work in 90 days, B in 40 days and C in 12 days. They work for a day each in turn i.e., first day A does it alone, B does it the second day and C the third day. After that A does it for another day, and so on. After finishing the work they get Rs. 240. If the wages are divided in proportion to the work done by them, find what each will get ?
a) A Rs. 24, B Rs. 54, C Rs. 162
b) A Rs. 22, B Rs.50, C Rs. 132
c) A Rs. 26, B Rs. 52, C Rs. 142
d) A Rs. 20, B Rs. 44, C Rs. 182
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 3 days work}} \cr & = \frac{1}{{90}} + \frac{1}{{40}} + \frac{1}{{12}} \cr & = \frac{{43}}{{360}} \cr & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 24 days work}} \cr & = \frac{{43}}{{360}} \times 8 \cr & = \frac{{344}}{{360}} \cr & {\text{Remaining work}} \cr & = \left( {1 - \frac{{344}}{{360}}} \right) \cr & = \frac{{16}}{{360}} \cr & = \frac{4}{{90}} \cr & {\text{On 25th day, it is A's turn}}{\text{.}} \cr & {\text{A's 1 day's work}} = \frac{1}{{90}} \cr & {\text{Remaining work}} \cr & = \left( {\frac{4}{{90}} - \frac{1}{{90}}} \right) \cr & = \frac{3}{{90}} \cr & = \frac{1}{{30}} \cr & {\text{On 26th day, it is B's turn}}{\text{.}} \cr & {\text{B's 1 day's work}} = \frac{1}{{40}} \cr & {\text{Remaining work}} \cr & = \left( {\frac{1}{{30}} - \frac{1}{{40}}} \right) \cr & = \frac{1}{{120}} \cr & {\text{On 27th day, it is C's turn}}{\text{.}} \cr & \frac{1}{{12}}{\text{ work is done by C in 1 day}}{\text{.}} \cr & \frac{1}{{120}}{\text{ work is done by C in }} \cr & = \left( {12 \times \frac{1}{{120}}} \right) \cr & = \frac{1}{{10}}{\text{ day}}{\text{.}} \cr} $$
Hence, the whole work is complete in $${\text{26}}\frac{1}{{10}}$$ days out of which A worked for 9 days,
B worked for 9 days and C worked for $${\text{8}}\frac{1}{{10}}$$ days.
Ratio of wages of A, B and C = Ratio of work done by A, B and C
$$ = \left( {\frac{1}{{90}} \times 9} \right):\left( {\frac{1}{{40}} \times 9} \right)$$ : $$\left( {\frac{1}{{12}} \times 8\frac{1}{{10}}} \right)$$
$$\eqalign{ & = \frac{1}{{10}}:\frac{9}{{40}}:\frac{{27}}{{40}} \cr & = 4:9:27 \cr & \therefore {\text{A's share}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{4}{{40}} \times 240} \right) \cr & = {\text{Rs}}{\text{.24}} \cr & {\text{B's share}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{9}{{40}} \times 240} \right) \cr & = {\text{Rs}}.54 \cr & {\text{C's share}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{{27}}{{40}} \times 240} \right) \cr & = {\text{Rs}}{\text{.162}} \cr} $$
38. A job can be done by 3 skilled workmen in 20 days or by 5 boys in 30 days. How many days will they take if they work together ?
a) 8 days
b) 10 days
c) 11 days
d) 12 days
Explanation:
$$\eqalign{ & {\text{3 men's 1 day's work}} = \frac{1}{{20}} \cr & {\text{5 boy's 1 day's work}} = \frac{1}{{30}} \cr & \left( {{\text{3 men}} + {\text{5 boy}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{20}} + \frac{1}{{30}}} \right) \cr & = \frac{5}{{60}} \cr & = \frac{1}{{12}} \cr} $$
∴ 3 men and 5 boys will complete the work in 12 days.
39. P is thrice as good a workman as Q and therefore able to finish a job in 48 days less than Q. Working together, they can do it in ?
a) 18 days
b) 24 days
c) 30 days
d) 12 days
Explanation: Let time taken by P = x days
Then, time taken by Q = 3x days
∴ 3x - x = 48
⇒ 2x = 48
⇒ x = 24
∴ (P + Q)'s 1 day's work
$$\eqalign{ & = \frac{1}{{24}} + \frac{2}{{72}} \cr & = \frac{{3 + 1}}{{72}} \cr & = \frac{1}{{18}} \cr} $$
∴ Required time = 18 days
40. A does 20% less work than B. If A can complete a piece of work in $$7\frac{1}{2}$$ hours, then B can do it in ?
a) $${\text{6}}\frac{1}{2}{\text{ hours}}$$
b) 6 hours
c) $${\text{5}}\frac{1}{2}{\text{ hours}}$$
d) 5 hours
Explanation: Let time taken by B = x
$${\text{Efficiency}} \propto \frac{1}{{{\text{Time}}\,{\text{taken}}}}$$
So, if B is 100% efficient. then A is 80% efficient
So,
$$\eqalign{ & \Rightarrow \frac{{80}}{{100}} = \frac{x}{{15/2}} \cr & \Rightarrow x = \frac{{80 \times 15}}{{100 \times 2}} \cr & \Rightarrow x = 6\,{\text{hours}} \cr} $$
41. A can do a piece of work in 12 days and B in 20 days. If they together work on it for 5 days, and remaining work is completed by C in 3 days, then in how many days can C do the same work alone ?
a) 10 days
b) 9 days
c) 12 days
d) 15 days
Explanation: L.C.M. of Total Work =60 unit
One day work of A = $$\frac{{60}}{{12}}$$ = 5 unit/day
One day work of B = $$\frac{{60}}{{20}}$$ = 3 unit/day
$$\eqalign{ & {\text{5}}\left( {{\text{A}} + {\text{B}}} \right) + {\text{3C}} = {\text{60 units}} \cr & {\text{5}} \times {\text{8}} + {\text{3C}} = 60 \cr & 3{\text{C}} = 20 \cr & {\text{C}} = \frac{{20}}{3}{\text{ units/day}} \cr & {\text{Time taken by C}} \cr & = \frac{{60}}{{\frac{{20}}{3}}} \cr & = \frac{{60 \times 3}}{{20}} \cr & = 9{\text{ days}} \cr} $$
42. A and B work together to complete the rest of a job in 7 days. However,$$\frac{{37}}{{100}}$$ of the job was already done. Also the work done by A in 5 days is equal to the work done by B in 4 days. How many days would be required by the fastest worker to complete the entire work ?
a) 20
b) 25
c) 30
d) 10
Explanation:
$$\eqalign{ & {\text{Total work}} = 100 \cr & {\text{Remaining work}} \cr & = 100 - 37 \cr & = 63 \cr & {\text{5A}} = {\text{4B}} \cr & \frac{{\text{A}}}{{\text{B}}} = \frac{4}{5}{\text{ efficiency}} \cr & {\text{Total efficiency of A}} + {\text{B}} = 9 \cr & {\text{Work done by in 7 days}} \cr & = 9 \times 7 \cr & = 63 \cr & \therefore {\text{Time taken by B}} \cr & = \frac{{100}}{5} \cr & = 20{\text{ days}} \cr} $$
43. A can do a work in 10 days. The efficiency of A is 20% less than B. How many days B need to finish the same work?
a) 8.5 days
b) 12.3 days
c) 8 days
d) 7.5 days
Explanation:
$$\eqalign{ & 20\% = \frac{1}{5}\left[ {{\text{efficiency}} \propto \frac{1}{{{\text{days}}}}} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{A }}:{\text{ B}} \cr & {\text{Efficiency}}\,\,\,\,\,\,4{\text{ }}:{\text{ }}5 \cr & {\text{Days}}\,\,\,\,\,\,\,\,\,\,\mathop {\mathop 5\limits_{{\text{ }} \downarrow \times 2} }\limits_{10\,{\text{days}}} :\mathop {\mathop 4\limits_{{\text{ }} \downarrow \times 2} }\limits_{{\bf{8}}\,{\bf{days}}} \cr} $$
44. A group of workers can complete a piece of work in 50 days, when they are working individually. On the first day one person works, on the second day another person joins him, on the third day one person joins them and this process continues till the work is completed. How many approximate days are needed to complete the work ?
a) 8 days
b) 9 days
c) 10 days
d) 11 days
Explanation: Let a man complete 1 piece of work in a day.
Then total work = 50 units
Then by statement 1 st day = one man × 1 work/day = 1
Then by statement 2nd day = two men × 1 work/day = 2
Then by statement 3rd day = three men × 1 work/day = 3
Let the whole work will be completed in N days.
Then total work 1 + 2 + 3 + ..... + N = 50
$$\eqalign{ & \frac{{{\text{N}}\left( {{\text{N}} + {\text{1}}} \right)}}{2} = 50 \cr & {\text{N}}\left( {{\text{N + 1}}} \right){\text{ = 100}} \cr & {\text{Then, N}} = 10{\text{ days}}\left( {{\text{approx}}} \right) \cr} $$
45. A can do a piece of work in 20 days and B in 15 days. With help of C, they finish the work in 5 days. In how many days C alone can do the same work ?
a) 5 days
b) 6 days
c) 10 days
d) 12 days
Explanation:L.C.M. of Total Work =60
One day work of A = $$\frac{{60}}{{20}}$$ = 3 unit/day
One day work of B = $$\frac{{60}}{{15}}$$ = 4 unit/day
One day work of A + B + C = $$\frac{{60}}{{5}}$$ = 12 unit/day
$$\eqalign{ & {\text{C's efficiency}} \cr & = 12 - 3 - 4 \cr & = 5 \cr & {\text{C will complete total work in}} \cr & = \frac{{60}}{5} \cr & {\text{ = 12 days}} \cr} $$
46. Shashi can do piece of work in 20 days. Tanya is 25% more efficient than Sashi. The number of days taken by Tanya to do the same piece of work is = ?
a) 15
b) 25
c) 18
d) 16
Explanation:
$$\eqalign{ & 25\% = \frac{1}{4}\left[ {{\text{efficiency}} \propto \frac{1}{{{\text{days}}}}} \right] \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{Sashi }}:{\text{ Tanya}} \cr & {\text{Efficiency}}\,\,\,\,\,\,\,4{\text{ }}:{\text{ }}5 \cr & {\text{Days}}\,\,\,\,\,\,\,\,\,\,\,\mathop {\mathop 5\limits_{{\text{ }} \downarrow \times 4} }\limits_{20} :\mathop {\mathop 4\limits_{{\text{ }} \downarrow \times 4} }\limits_{{\bf{16}}} \cr} $$
47. 18 men or 36 boys working 6 hours a day can plough a field in 24 days. In how many days will 24 men and 24 boys working 9 hours a day plough the same field ?
a) 9 days
b) 10 days
c) 6 days
d) 8 days
Explanation:Let the required no of days be x.
18 Men = 36 Boys
1 Man = 2 Boys
∴ 24 Men = 48 Boys
According to the question,
M1D1H1 = M2D2H2
36 × 24 × 6 = (48 + 24) × x × 9
36 × 24 × 6 = 72 × 9 × x
x = $$\frac{{36 \times 6 \times 24}}{{72 \times 9}}$$
x = 8 days
48. A can do $$\frac{1}{3}$$ rd of a work in 5 days and B can do the do $$\frac{2}{5}$$ th of this work in 10 days. Both A and B, together can do the work in ?
a) $${\text{ 7}}\frac{3}{8}{\text{ days}}$$
b) $${\text{8}}\frac{4}{5}{\text{ days}}$$
c) $${\text{9}}\frac{3}{8}{\text{ days}}$$
d) 10 days
Explanation:
$$\eqalign{ & \frac{1}{3}{\text{work in 5 days}} \cr & {\text{then a complete work in}} \cr & = 5 \times 3 = 15{\text{ days}} \cr & {\text{B}} \to \frac{2}{5}{\text{work in 10 days}} \cr & {\text{then B completes work in}} \cr & = 10 \times \frac{5}{2} = {\text{25 days}} \cr} $$
L.C.M. of Total Work =75
One day work of A = $$\frac{{75}}{{15}}$$ = 5 unit/day
One day work of B = $$\frac{{75}}{{25}}$$ = 3 unit/day
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{ can do work}} \cr & = \frac{{75}}{8} = 9\frac{3}{8}{\text{ days}} \cr} $$
49. A and B undertake a piece of work for Rs. 250. A alone can do that work in 5 days and B alone can do that work in 15 days. With the help of C, they finish the work in 3 days. If every one gets paid in proportion to work done by them, the amount C will get is ?
a) Rs. 50
b) Rs. 100
c) Rs. 150
d) Rs. 200
Explanation: L.C.M. of Total Work = 45
One day work of A = $$\frac{{45}}{{5}}$$ = 9 unit/day
One day work of B = $$\frac{{45}}{{15}}$$ = 3 unit/day
One day work of A + B + C = $$\frac{{45}}{{3}}$$ = 15 unit/day
$$\eqalign{ & {\text{Efficiency of C}} \cr & = 15 - \left( {9 + 3} \right) \cr & = 3 \cr & {\text{C's amount}} \cr & = \frac{{250}}{{15}} \times 3 \cr & = {\text{Rs}}{\text{. 50}} \cr} $$
50. A is twice as good as B and together they finish a piece of work in 16 days. The number of days taken by A alone to finish the work is = ?
a) 20 days
b) 21 days
c) 22 days
d) 24 days
Explanation:
$$\eqalign{ & {\text{B}}:{\text{A}} \cr & \,1:2 \to {\text{Efficiency ratio}} \cr & {\text{Total work}} = 16 \times \left( {1 + 2} \right) = 48 \cr} $$
Number of days taken by A to complete the work
$$\eqalign{ & = \frac{{48}}{2} \cr & = 24{\text{ days}} \cr} $$
51. A contractor was engaged to construct a road in 16 days. After working for 12 days with 20 labours it was found that only $${\frac{5}{8}}$$ th of the road had been constructed. To complete the work in stipulated time the number of extra labours required are ?
a) 16
b) 12
c) 10
d) 18
Explanation:
$$\eqalign{ & {\text{From, }} \cr & \frac{{{{\text{m}}_1} \times {{\text{d}}_1} \times {{\text{t}}_1}}}{{{{\text{w}}_1}}} = \frac{{{{\text{m}}_2} \times {{\text{d}}_2} \times {{\text{t}}_2}}}{{{{\text{w}}_2}}} \cr & {\text{Let extra workers be x}} \cr & \Rightarrow \frac{{20 \times 12}}{{\frac{5}{8}}} = \frac{{\left( {20 + x} \right) \times 4}}{{\frac{3}{8}}} \cr & \Rightarrow 4 \times 12 = \frac{{\left( {20 + x} \right) \times 4}}{3} \cr & \Rightarrow 36 = 20 + x \cr & \Rightarrow x = 16 \cr & \Rightarrow {\text{Extra workers }} = {\text{16}} \cr} $$
52. A alone can complete a piece of work in 18 days and B alone in 15 days, B alone worked at it for 10 days and then left the work. In how many more days, will A alone complete the remaining work ?
a) 5 days
b) $${\text{5}}\frac{1}{2}{\text{ days}}$$
c) 6 days
d) 8 days
Explanation:
$$\eqalign{ & {\text{B's}}\,{\text{10}}\,{\text{day's}}\,{\text{work}} \cr & = \left( {\frac{1}{{15}} \times 10} \right) = \frac{2}{3} \cr & {\text{Remaining}}\,{\text{work}} \cr & = \left( {1 - \frac{2}{3}} \right) = \frac{1}{3} \cr & {\text{Now}},\frac{1}{{18}}{\text{work}}\,{\text{is}}\,{\text{done}}\,{\text{by}}\,{\text{A}}\,{\text{in}}\,{\text{1}}\,{\text{day}} \cr & \therefore \frac{1}{3}\,{\text{work}}\,{\text{is}}\,{\text{done}}\,{\text{by}}\,{\text{A}}\,{\text{in}} \cr & \left( {18 \times \frac{1}{3}} \right) = 6\,{\text{days}} \cr} $$
53. A can do a piece of work in 12 days. When he had worked for 3 days. B joined him. If they complete the work in 3 more days, in how many days can B alone finish the work ?
a) 6 days
b) 12 days
c) 4 days
d) 8 days
Explanation: Total work = 12
Efficiency 1 units/day = 12 days time (A)
After 3 days A finishes 3 units.
∴ Work left =12 - 3 = 9 units
9 units of work, 3 units/day = 3 days (A + B)
(A + B)'s one day work = 3 units
A's one day work = 1 unit
B's one day work = 3 - 1 = 2 units
∴ B completes whole work in
$$\eqalign{ & = \frac{{{\text{Total work}}}}{{{\text{Efficiency}}}} \cr & = \frac{{12}}{2} \cr & = {\text{6 days }} \cr} $$
54. 45 men can complete a piece of work in 16 days. Four days they started working , 36 more men joined them. How many days will they take to complete the remaining work ?
a) 6 days
b) 8 days
c) $${\text{6}}\frac{2}{3}{\text{ days}}$$
d) $${\text{7}}\frac{3}{4}{\text{ days}}$$
Explanation: According to the question,
Let the remaining work is complete in D days
$${\text{4}}{{\text{5}}_{{\text{men}}}} \times {\text{1}}{{\text{6}}_{{\text{days}}}}$$ = $$\left( {{\text{4}}{{\text{5}}_{{\text{men}}}} \times {{\text{4}}_{{\text{days}}}}} \right)$$ + $${\left( {{\text{45}} + {\text{36}}} \right)_{{\text{men}}}}$$ $$ \times {\text{D}}$$
$$\eqalign{ & \Rightarrow \frac{{540}}{{81}} = {\text{D}} \cr & \Rightarrow {\text{D}} = 6\frac{2}{3}{\text{ days}} \cr} $$
55. A started a ,work and left after working for 2 days. Then B was called and he finished the work in 9 days. had A left the work after working for 3 days, B would have finished the remaining work in 6 days. In how many days can each of them, working alone, finish the whole work ?
a) 2.5 days, 7.5 days
b) 5 days, 8.5 days
c) 5 days, 15 days
d) None of these
Explanation: Suppose A takes x days to finish the work alone and B take y days to finish the work alone.
$$\eqalign{ & {\text{Then,}}\frac{2}{x} + \frac{9}{y} = 1.....(i) \cr & {\text{And,}}\frac{3}{x} + \frac{6}{y} = 1 \cr & \Leftrightarrow \frac{1}{x} + \frac{2}{y} = \frac{1}{3} \cr & \Leftrightarrow \frac{2}{x} + \frac{4}{y} = \frac{2}{3}.....({\text{ii)}} \cr & {\text{Subtracting (ii) from (i), }} \cr & {\text{We get}}:\frac{5}{y} = \frac{1}{3}{\text{or }}y = 15 \cr & {\text{Putting }}y = 15{\text{ in (i), }} \cr & {\text{We get}}:\frac{2}{x} = \frac{2}{5}{\text{or }}x = 5 \cr} $$
Hence, A alone takes 5 days while B alone takes 15 days to finish the work.
56. A company employed 200 workers to complete a certain work in 150 days. If only $$\frac{1}{4}$$ th of the work had been done in 50 days, then in order to complete the whole work in time, the number of additional workers to be employed were ?
a) 100
b) 600
c) 300
d) 200
Explanation:
$$\eqalign{ & \Rightarrow \frac{{{{\text{M}}_1}{{\text{D}}_1}}}{{{{\text{W}}_1}}} = \frac{{{{\text{M}}_2}{{\text{D}}_2}}}{{{{\text{W}}_2}}} \cr & \Rightarrow \frac{{200 \times 50}}{{\frac{1}{4}}} = \frac{{{{\text{M}}_2} \times 100}}{{\frac{3}{4}}} \cr & \Rightarrow {{\text{M}}_2} = 300 \cr & {\text{So, additional men}} \cr & = 300 - 200 \cr & = 100 \cr} $$
57. If 20 women can lay a road of length 100m in 10 days. 10 women can lay the same road of length 50m in = ?
a) 5 days
b) 15 days
c) 10 days
d) 20 days
Explanation:
$$\eqalign{ & {\text{According to the question,}} \cr & \frac{{20 \times 10}}{{100}} = \frac{{10 \times x}}{{50}} \cr & \Leftrightarrow x = 10{\text{ days}} \cr} $$
58. A and B can together finish a work in 30 days. They worked together for 20 days and B left. After another 20 days, A finished the remaining work. In how many days A alone can finish the job ?
a) 40 days
b) 50 days
c) 54 days
d) 60 days
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 20 day's work}}{\text{.}} \cr & = \left( {\frac{1}{{30}} \times 20} \right) \cr & = \frac{2}{3} \cr & {\text{Remaining work }} \cr & = \left( {1 - \frac{2}{3}} \right) \cr & = \frac{1}{3}{\text{ }} \cr} $$
Now, $$\frac{1}{3}$$ work is done by A in 20 days
Whole work will be done by A in (20 × 3) = 60 days.
59. A can build up a wall in 8 days while B can break it in 3 days. A has worked for 4 days and then B joined to work with A for another 2 days only. In how many days will A alone build up the remaining part of the wall ?
a) $${\text{6}}\frac{1}{3}{\text{ days}}$$
b) 7 days
c) $${\text{7}}\frac{1}{3}{\text{ days}}$$
d) $${\text{13}}\frac{1}{3}{\text{ days}}$$
Explanation: Part of wall built by A in 1 day = $$\frac{1}{8}$$
Part of wall broken by B in 1 day = $$\frac{1}{3}$$
Part of wall built by A in 4 days
$$\eqalign{ & = \left( {\frac{1}{8} \times 4} \right) \cr & = \frac{1}{2} \cr} $$
Part of wall broken by B and built by A in 2 days
$$\eqalign{ & = 2\left( {\frac{1}{3} - \frac{1}{8}} \right) \cr & = \frac{5}{{12}} \cr} $$
$$\eqalign{ & {\text{Part of wall built in 6 days}} \cr & = \left( {\frac{1}{2} - \frac{5}{{12}}} \right) \cr & = \frac{1}{{12}} \cr & {\text{Remaining part to be built}} \cr & = \left( {1 - \frac{1}{{12}}} \right) \cr & = \frac{{11}}{{12}} \cr} $$
Now, $$\frac{1}{8}$$ part of wall built by A in 1 day
$$\eqalign{ & \therefore \frac{{11}}{{12}}{\text{ part of wall built by A in}} \cr & = \left( {8 \times \frac{{11}}{{12}}} \right) \cr & = \frac{{22}}{3} \cr & = 7\frac{1}{3}{\text{ day}} \cr} $$
60. Anuj and Manoj can together paint their house in 30 days. After working for 20 days, Anuj has to go out and Manoj finished the remaining working the next 30 days. If Manoj had gone away after 20 days instead of Anuj, then Anuj would have completed the remaining work in ?
a) 15 days
b) 20 days
c) 25 days
d) 35 days
Explanation:
$$\eqalign{ & \left( {{\text{Anuj}} + {\text{Manoj}}} \right){\text{'s 20 day's work}} \cr & = \left( {\frac{1}{{30}} \times 20} \right) \cr & = \frac{2}{3} \cr & {\text{Remaining work}} \cr & = \left( {1 - \frac{2}{3}} \right) \cr & = \frac{1}{3} \cr & {\text{Manoj's 30 day's work}} = \frac{1}{3} \cr & \therefore {\text{Manoj's 1 day's work}} = \frac{1}{{90}} \cr & {\text{Anuj's 1 day's work}} \cr & = \left( {\frac{1}{{30}} - \frac{1}{{90}}} \right) \cr & {\text{ = }}\frac{2}{{90}} \cr & = \frac{1}{{45}} \cr} $$
If Manoj had gone away after 20 days, then the remaining $$\frac{1}{3}$$ work would have been done by Anuj.
$$\frac{1}{{45}}$$ work is done by Anuj in 1 day
$$\frac{1}{3}$$ work would be done by Anuj in
$$\eqalign{ & = \left( {45 \times \frac{1}{3}} \right) \cr & = {\text{15 days}} \cr} $$
61. 40 men can complete a piece of work in 18 days. Eight days after they started working together, 10 more men joined them. How many days will they now take to complete the remaining work ?
a) 6 days
b) 8 days
c) 10 days
d) 12 days
Explanation: Let D days required to complete the remaining work
$${40_{{\text{men}}}} \times {18_{{\text{days}}}}$$ = $$\left( {{{40}_{{\text{men}}}} \times {8_{{\text{days}}}}} \right)$$ + $$\left( {{{50}_{{\text{men}}}} \times {\text{D}}} \right)$$
$$\eqalign{ & \Rightarrow 720 - 320 = 50{\text{D}} \cr & \Rightarrow {\text{D}} = 8 \cr} $$
62. A, B and C can complete a work in 10, 12 and 15 days respectively. They started the work together. But A left the work 5 days before its completion. B also left the work 2 days after A left. In how many days was the work completed ?
a) 4
b) 5
c) 7
d) 8
Explanation:
$$\eqalign{ & {\text{C's 3 day's work}} \cr & = \left( {\frac{1}{{15}} \times 3} \right) \cr & = \frac{1}{5} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 2 day's work}} \cr & = \left[ {\left( {\frac{1}{{12}} + \frac{1}{{15}}} \right) \times 2} \right] \cr & = \left( {\frac{3}{{20}} \times 2} \right) \cr & = \frac{3}{{10}} \cr & \therefore {\text{Remaining work}} \cr & = \left[ {1 - \left( {\frac{1}{5} + \frac{3}{{10}}} \right)} \right] \cr & = \left( {1 - \frac{1}{2}} \right) \cr & = \frac{1}{2} \cr & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{10}} + \frac{1}{{12}} + \frac{1}{{15}}} \right) \cr & = \frac{{15}}{{60}} \cr & = \frac{1}{4} \cr} $$
$$\frac{1}{4}$$ work is done by A, B ans C in 1 day.
∴ $$\frac{1}{2}$$ work is done by A, B and C in
$$\eqalign{ & = \left( {4 \times \frac{1}{2}} \right) \cr & = {\text{2 days}} \cr & {\text{Total number of days}} \cr & = \left( {3 + 2 + 2} \right) \cr & = 7 \cr} $$
63. A man and a boy received Rs. 800 as wages for 5 days for the work they did together. The man's efficiency in the work was three times that of the boy. What are the daily wages of the boy ?
a) Rs. 40
b) Rs. 44
c) Rs. 56
d) Rs. 76
Explanation: Ratio of 1 day's work of man and boy = 3 : 1
$$\eqalign{ & {\text{Total wages of the boy}} \cr & = {\text{Rs}}{\text{.}}\left( {800 \times \frac{1}{4}} \right) \cr & = {\text{Rs}}{\text{. 200}} \cr & \therefore {\text{Daily wages of the boy}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{{200}}{5}} \right) \cr & = {\text{Rs}}{\text{. 40}} \cr} $$
64. Two men undertake to do a piece of work for Rs. 1400. The first man alone can do this work in 7 days while the second man alone can do this work in 8 days. If they working together complete this work in 3 days with the help of a boy, how should the money be divided ?
a) Rs. 600, Rs. 550, Rs. 250
b) Rs. 600, Rs. 525, Rs. 275
c) Rs. 600, Rs. 500, Rs. 300
d) Rs. 500, Rs. 525, Rs. 375
Explanation:
$$\eqalign{ & {\text{Boy's 1 day's work}} \cr & = \frac{1}{3} - \left( {\frac{1}{7} + \frac{1}{8}} \right) \cr & = \left( {\frac{1}{3} - \frac{{15}}{{56}}} \right) \cr & = \frac{{11}}{{168}} \cr} $$
∴ Ratio of wages of the first man, second man and boy
$$\eqalign{ & = \frac{1}{7}:\frac{1}{8}:\frac{{11}}{{168}} \cr & = 24:21:11 \cr & {\text{First man's share}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{{24}}{{56}} \times 1400} \right) \cr & = {\text{Rs}}{\text{.600}} \cr & {\text{Second man's share}} \cr & = {\text{Rs}}{\text{.}}\left( {\frac{{21}}{{56}} \times 1400} \right) \cr & = {\text{Rs}}{\text{.525}} \cr & {\text{Boy's man's share}} \cr & = {\text{Rs}}{\text{.}}\left[ {1400 - \left( {600 + 525} \right)} \right] \cr & = {\text{Rs}}{\text{.275}} \cr} $$
65. 20 men can do a piece of work in 18 days. They worked together for 3 days, then 5 men joined. In how many days is the remaining work completed ?
a) 12 days
b) 14 days
c) 13 days
d) 15 days
Explanation: 20 men → 18 days
⇒ Work done by 20 men working
Together = 1 work
⇒ Work done by them in 3 days working
Together = 1 × 3 = 3 work
⇒ Remaining work = 18 - 3 = 15 work
⇒ 15 work is to be done by (20 + 5) = 25 men
$$\eqalign{ & \therefore {\text{Efficiency of 1 man}} = \frac{1}{{20}} \cr & \Rightarrow {\text{Efficincy of 5 men}} \cr & = \frac{5}{{20}} \cr & = \frac{1}{4} \cr & \Rightarrow {\text{So, efficiency of }}\left( {20 + 5} \right) \cr & \Rightarrow 25{\text{ men}} = 1 + \frac{1}{4} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{5}{4}{\text{ working days}} \cr & {\text{Required time}} \cr & = \frac{{{\text{Work}}}}{{{\text{Efficiency}}}} \cr & = \frac{{15}}{{\frac{5}{4}}} \cr & = 12{\text{ days}} \cr} $$
Therefore, 12 more days will be taken to finish the remaining work
66. A and B can do a work in 8 days, B and C can do the same work in 12 days. A, B and C together can finish it in 6 days. A and C together will do it in = ?
a) 8 days
b) 6 days
c) 8 days
d) 12 days
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{6} \cr & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{8} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{{12}}{\text{ }} \cr & \therefore \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {2 \times \frac{1}{6}} \right) - \left( {\frac{1}{8} + \frac{1}{{12}}} \right) \cr & = \left( {\frac{1}{3} - \frac{5}{{24}}} \right) \cr & = \frac{3}{{24}} \cr & = \frac{1}{8} \cr} $$
So, A and C together will do the work in 8 days.
67. A and B together can do a job in 2 days; B and C can do it in 4 days; A and C in $${\text{2}}\frac{2}{5}$$ days. The number of days required for A to do the job alone is = ?
a) 1
b) 3
c) 6
d) 12
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{2} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{4} \cr & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{5}{{12}} \cr & {\text{Adding, we get: }} \cr & {\text{2}}\left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{2} + \frac{1}{4} + \frac{1}{{12}}} \right) \cr & = \frac{{14}}{{12}} \cr & = \frac{7}{6} \cr & \Rightarrow \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{7}{{12}} \cr & {\text{So, A's 1 day's work}} \cr & = \left( {\frac{7}{{12}} - \frac{1}{4}} \right) \cr & = \frac{4}{{12}} \cr & = \frac{1}{3} \cr & \therefore {\text{A alone can do the work in 3 days}}{\text{.}} \cr} $$
68. 10 men working 6 hours a day can complete a work in 18 days. How many hours a day must 15 men work to complete the same work in 12 days ?
a) 6 hours/day
b) 10 hours/day
c) 12 hours/day
d) 15 hours/day
Explanation:
$$\eqalign{ & \frac{{{{10}_{{\text{men}}}} \times {6_{{\text{hours}}}} \times {{18}_{{\text{days}}}}}}{{{1_{{\text{work}}}}}} = \frac{{{{15}_{{\text{men}}}} \times {{12}_{{\text{days}}}} \times {\text{H hour/day}}}}{{{1_{{\text{work}}}}}} \cr & \Leftrightarrow {\text{6 hours/day}} \cr} $$
69. A work could be completed in 100 days by some workers. However, due to the absence of 10 workers, it was completed in 110 days. The original number of workers was ?
a) 100
b) 110
c) 55
d) 50
Explanation: Let total number of worker in beginning is N
$$\eqalign{ & {\text{According to the question,}} \cr & \frac{{{\text{N}} \times {{100}_{{\text{days}}}}}}{{{1_{{\text{work}}}}}} = \frac{{\left( {{\text{N}} - 10} \right) \times {{110}_{{\text{days}}}}}}{{{1_{{\text{work}}}}}} \cr & 100{\text{N}} = {\text{110N}} - {\text{1100}} \cr & \Rightarrow {\text{10N}} = {\text{1100}} \cr & \Rightarrow {\text{N}} = {\text{110}} \cr} $$
70. A job can be complete by 12 men in 12 days. How many extra days will be needed to complete the job if 6 men leave after working for 6 days ?
a) 3 days
b) 6 days
c) 12 days
d) 24 days
Explanation: According to the question,
Total work
= 12 M × 12 D
= 144 units
Work done by 12 men in 6 days
= 12 × 6
= 72 units
Rest work
= 144 - 72
= 72 units
Required time for 6 men to complete the work
$$\eqalign{ & = \frac{{72}}{6} \cr & {\text{ = 12 days}} \cr & {\text{Hence,}} \cr & {\text{Total time}} = 12 + 6 = 18{\text{ days}} \cr & {\text{Extra time}} = 18 - 12 = 6{\text{ days}} \cr} $$
71. 3 men or 5 women can do a work in 12 days. How long will 6 men and 5 women take to finish the work ?
a) 20 days
b) 10 days
c) 4 days
d) 15 days
Explanation: According to the question,
3 men = 5 women
As they complete the same work in same time
6 men + 5 women
= 6 men + 3 men
= 9 men
If, 3 men does a work in 12 days
1 men does a work in 12 × 3
9 men does a work in $$\frac{{{\text{12}} \times {\text{3}}}}{9}$$ = 4 days
72. A particular job can be completed by a team of 10 men in 12 days. The same job can be completed by a team of 10 women in 6 days. How many days are needed to complete the job if the two teams work together ?
a) 4 days
b) 6 days
c) 9 days
d) 18 days
Explanation:
$$\eqalign{ & {\text{10 men}} \times {\text{12 days}} = {\text{10 women}} \times {\text{6 days}} \cr & {\text{2 men}} = {\text{1 woman}} \cr & \frac{{\text{M}}}{{\text{W}}} = \frac{1}{2}{\text{ }} \cr & {\text{1 man work}} = {\text{1 unit/day}} \cr & {\text{1 woman work}} = {\text{2 unit/day}} \cr & {\text{Total work}} = {\text{10 men}} \times {\text{12 days}} \cr & = 10 \times 1 \times 12 \cr & = 120{\text{ units}} \cr & {\text{Time required}}\left( {{\text{10 men}} + {\text{10 women}}} \right) \cr & = \frac{{{\text{Total work}}}}{{{\text{Efficiency}}}} \cr & = \frac{{120}}{{10 \times 1 + 10 \times 2}} \cr & = \frac{{120}}{{30}} \cr & = 4{\text{ days}} \cr} $$
73.Two workers A and B are engaged to do a work. A working alone takes 8 hours more to complete the job than if both worked together. If B worked alone, he would need 41/2 hours more to complete the job than they both working together. What time would they take to do the work together ?
a) 4 hours
b) 5 hours
c) 6 hours
d) 7 hours
Explanation: Let A and B together take x hours to complete the work.
Then, A alone takes (x + 8) hours
And
B alone takes $$\left( {{\text{x}} + \frac{9}{2}} \right)$$ hours to complete the work
Then,
$$\eqalign{ & \Rightarrow \frac{1}{{\left( {x + 8} \right)}} + \frac{1}{{\left( {x + \frac{9}{2}} \right)}} = \frac{1}{x} \cr & \Rightarrow \frac{1}{{\left( {x + 8} \right)}} + \frac{2}{{\left( {2x + 9} \right)}} = \frac{1}{x} \cr & \Rightarrow x\left( {4x + 25} \right) = \left( {x + 8} \right)\left( {2x + 9} \right) \cr & \Rightarrow 2{x^2} = 72 \cr & \Rightarrow {x^2} = 36 \cr & \Rightarrow x = 6 \cr} $$
74. Three friends Anne, Bob and Chris work together to do a certain job. Time it takes them to do the work together to do a certain job. The it takes them to do the work together is 6 hours less than Anne would have take alone, 1 hour less than Bob would have taken alone and half the time Chris would have taken working alone text. How long did it take them to complete the job, working together ?
a) 20 minutes
b) 30 minutes
c) 40 minutes
d) 50 minutes
Explanation: Let the time taken by the three friends together to do the work be x hours
Then, time taken by Anne alone = (x + 6) hours
Time taken by Bob alone = (x + 1) hours
Time taken by Bob alone = 2x hours
$$\therefore \frac{1}{{x + 6}} + \frac{1}{{x + 1}} + \frac{1}{{2x}} = \frac{1}{x}$$
$$ \Rightarrow $$ $$\frac{{2x\left( {x + 1} \right) + 2x\left( {x + 6} \right) + \left( {x + 1} \right)\left( {x + 6} \right)}}{{2x\left( {x + 6} \right)\left( {x + 1} \right)}}$$ $$ = $$ $$\frac{1}{x}$$
$$\eqalign{ & \Rightarrow 5{x^2} + 21x + 6 = 2\left( {{x^2} + 7x + 6} \right) \cr & \Rightarrow 3{x^2} + 7x - 6 = 0 \cr & \Rightarrow \left( {x + 3} \right)\left( {3x - 2} \right) = 0 \cr & \Rightarrow x = \frac{2}{3}{\text{ }}\left[ {\because x \ne - 3} \right] \cr & \therefore {\text{Required times}} \cr & = \frac{2}{3}{\text{ hours}} \cr & = \left( {\frac{2}{3} \times 60} \right){\text{hours}} \cr & = 40{\text{ minutes}} \cr} $$
75. A and B together can complete a work in 12 days. B and C together can complete the same work in 8 days and A and C together can complete it in 16 days. In total, how many days do A, B and C together take to complete the same work ?
a) $${\text{3}}\frac{5}{{12}}$$
b) $${\text{3}}\frac{9}{{13}}$$
c) $${\text{7}}\frac{5}{{12}}$$
d) $${\text{7}}\frac{5}{{13}}$$
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{{12}} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{8} \cr & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{{16}} \cr} $$
Adding, we get 2(A + B + C)'s 1 day's work
$$\eqalign{ & = \left( {\frac{1}{{12}} + \frac{1}{8} + \frac{1}{{16}}} \right) \cr & = \frac{{13}}{{96}} \cr} $$
So, A, B and C together can complete the work in
$$\eqalign{ & = \frac{{96}}{{13}} \cr & = 7\frac{5}{{13}}{\text{days}} \cr} $$
76. 60 men could complete a piece of work in 250 days. They worked together for 200 days. After that work had to be stopped for 10 days due to bad weather. How many more men should be engaged to complete the work in time ?
a) 10
b) 15
c) 18
d) 20
Explanation: 60 men work for 200 days.
They stops for 10 day due to bad weather.
So, the work is to complete in
= (50 - 10)
= 40 days
In order to complete in scheduled time i.e., 250 days.
Let 'n' number of more men is required
(60men × 200days) +{(60 + n)men × 40days} = 60men × 250days
⇒ 12000 + {(60 + n)men × 40days} = 15000
⇒ (60 + n)40days = 3000
⇒ 60 + n = 75
⇒ n = 15
77. A and B can do a piece of work in 12 days, B and C in 8 days and C and A in 6 days. How long would B take to do the same work alone ?
a) 24 days
b) 32 days
c) 40 days
d) 48 days
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{{12}} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{8} \cr & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 day's work}} = \frac{1}{{62}} \cr} $$
[ (A + B)'s 1 day's work + (B + C)'s 1 day's work ] - (A + C)'s 1 day's work
$$\eqalign{ & = \frac{1}{{12}} + \frac{1}{8} - \frac{1}{6} \cr & \Rightarrow 2\left( {{\text{B's 1 day's work}}} \right) = \frac{1}{{24}} \cr & \Rightarrow {\text{B's 1 day's work}} = \frac{1}{{48}} \cr} $$
Hence, B alone can do the work in 48 days.
78. A can build a wall in the same time in which B and C together can do it. If A and B together can do it. If A and B together could do it in 25 days and C alone in 35 days, in what time could B alone do it ?
a) 91 days
b) 100 days
c) 175 days
d) None of these
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{{25}} \cr & {\text{C's 1 day's work}} = \frac{1}{{35}} \cr & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{25}} + \frac{1}{{35}}} \right) \cr & = \frac{{12}}{{175}}.....({\text{i}}) \cr} $$
Also, A's 1 day's work = (B + C)'s 1 day's work.....(ii)
$$\eqalign{ & {\text{From (i) and (ii), we get : }} \cr & \Rightarrow {\text{2}} \times \left( {{\text{A's 1 day's work}}} \right) = \frac{{12}}{{175}} \cr & \Rightarrow {\text{A's 1 day's work}} = \frac{6}{{175}} \cr & \therefore {\text{B's 1 day's work}} \cr & = \left( {\frac{1}{{25}} - \frac{6}{{175}}} \right) \cr & = \frac{1}{{175}} \cr} $$
79. Madhu takes twice as much time as Uma to complete a work and Rahul does it in the same time as Madhu and Uma together. If all three working together can finish the work in 6 days, then the time taken by Madhu to finish the work is = ?
a) 12 days
b) 14 days
c) 36 days
d) 40 days
Explanation: Suppose Uma takes x days to complete a work
Then, Madhu takes 2x days to complete the work
Uma's 1 day's work = $$\frac{1}{x}$$
Madhu's 1 day's work = $$\frac{1}{{2x}}$$
Rahul's 1 day's work = (Madhu + Uma)'s 1 day's work
$$\eqalign{ & = \frac{1}{{2x}} + \frac{1}{x} \cr & = \frac{3}{{3x}}{\text{ }} \cr} $$
(Madhu + Uma + Rahul)'s 1 day's work
$$\eqalign{ & = \frac{3}{{3x}} + \frac{1}{{2x}} + \frac{1}{x} = \frac{6}{{3x}} = \frac{3}{x} \cr & \therefore \frac{3}{x} = \frac{1}{6} \cr & \Rightarrow x = 18{\text{ }} \cr} $$
Hence, Madhu takes (2 × 18) = 36 days to complete the work
80. If 28 men complete $$\frac{7}{8}$$ of a piece of work in a week, then the number of men, who must be engaged to get the remaining work completed in another week, is = ?
a) 5
b) 6
c) 4
d) 3
Explanation:
$$\eqalign{ & \frac{{{\text{28 M}} \times {\text{1 Week}}}}{{\frac{7}{8}}} = \frac{{x \times {\text{ 1 Week}}}}{{\frac{1}{8}}} \cr & \Leftrightarrow x = 4{\text{ men}} \cr} $$
81. A can complete a piece of work in 10 days, B in 15 days and C in 20 days. A and C together for 2 days and A was replaced by B. In how many days, altogether, was the work complete ?
a) 6 days
b) 8 days
c) 15 days
d) 16 days
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{10}} + \frac{1}{{20}}} \right) \cr & = \frac{3}{{20}} \cr & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 2 day's work}} \cr & = \left( {\frac{3}{{20}} \times 2} \right) \cr & = \frac{3}{{10}} \cr & {\text{Remaining work }} \cr & = \left( {1 - \frac{3}{{10}}} \right) \cr & = \frac{7}{{10}}{\text{ }} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{15}} + \frac{1}{{20}}} \right) \cr & = \frac{7}{{60}} \cr} $$
$$\frac{7}{{60}}$$ work is done by B and C in 1 day
∴ $$\frac{7}{{10}}$$ work is done by B and C in
$$\eqalign{ & = \left( {\frac{{60}}{7} \times \frac{7}{{10}}} \right) \cr & = 6{\text{ days}}{\text{. }} \cr & {\text{Hence, total time taken }} \cr & = \left( {2 + 6} \right){\text{days}} \cr & = 8{\text{ days}} \cr} $$
82. A completes $$\frac{7}{{10}}$$ of the work 15 days. Then he completes the remaining work the help of B in 4 days. The time required for A and B together to complete the entire work is = ?
a) $${\text{8}}\frac{1}{4}{\text{days}}$$
b) $$10\frac{1}{2}{\text{days}}$$
c) $$12\frac{2}{3}{\text{days}}$$
d) $$13\frac{1}{3}{\text{days}}$$
Explanation:
$$\eqalign{ & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 4 day's work}} \cr & = \left( {1 - \frac{7}{{10}}} \right) \cr & = \frac{3}{{10}} \cr & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{3}{{10}} \times \frac{1}{4}} \right) \cr & = \frac{3}{{40}} \cr & {\text{Remaining work }} \cr & = \left( {1 - \frac{3}{{10}}} \right) \cr & = \frac{7}{{10}}{\text{ }} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{15}} + \frac{1}{{20}}} \right) \cr & = \frac{7}{{60}} \cr} $$
Hence, A an B together take $$ = \frac{{40}}{3} = 13\frac{1}{2}$$ days to complete the entire work.
83. A man and a boy can do a piece of work in 24 days. If the man works alone for the last 6 days, it is completed in 26 days. How long would the boy take to do it alone ?
a) 20 days
b) 24 days
c) 36 days
d) 72 days
Explanation: (M + B)'s 1 day's work =$$\frac{1}{{24}}$$
(M + B)'s 20 day's work + M's 6 day's work = 1
$$\eqalign{ & \Rightarrow {\text{M's 6 day's work}} \cr & = \left( {1 - \frac{1}{{24}} \times 20} \right) \cr & = \frac{4}{{24}} = \frac{1}{6} \cr & \Rightarrow {\text{M's 1 day's work}} \cr & = \frac{1}{6} \times \frac{1}{6} \cr & = \frac{1}{{36}} \cr & \therefore {\text{B's 1 day's work}} \cr & = \frac{1}{{24}} - \frac{1}{{36}} \cr & = \frac{1}{{72}} \cr} $$
Hence, the boy alone can do the work in 72 days.
84. Two men can do a piece of work in x days. But y women can do that in 3 days. Then the ratio of the work done by 1 man and 1 woman is ?
a) 3y : 2x
b) 3x : 2y
c) x : y
d) 2y : 3x
Explanation: 2 men can do a work in x days
1 men can do a work in (2 × x) days
y women can do a work in 3 days
1 women can do a work in 3y days
| 1 man | : | 1 woman | |
| Days | 2x | : | 3y |
| Efficiency | 3y | : | 2x |
85. If 12 carpenters working 6 hours a day can make 460 chairs in 240 days, then number of chairs made by 18 carpenters in 360 days each working 8 hours a day ?
a) 1320
b) 1380
c) 1260
d) 920
Explanation:
$${\text{According to the question,}}$$
$$ \Rightarrow \frac{{12 \times 6 \times 240}}{{460}}$$ = $$\frac{{18 \times 360 \times 8}}{x}$$
$$\eqalign{ & \Rightarrow x = \frac{{18 \times 360 \times 8 \times 460}}{{12 \times 6 \times 240}} \cr & \Rightarrow x = 1380 \cr} $$
86. A and B can do a job in 7 days. A is $${\text{1}}\frac{3}{4}$$ times as efficient as B. The same job can be done by A alone in ?
a) $$9\frac{1}{3}\,{\text{days}}$$
b) $${\text{11 days}}$$
c) $$12\frac{1}{4}\,{\text{days}}$$
d) $$16\frac{1}{3}\,{\text{days}}$$
Explanation: (A's 1 day's work) : (B's 1 day's work)
$$\eqalign{ & = \frac{7}{4}:1 \cr & = 7:4 \cr} $$
Let A's and B's 1 day's work be 7x and 4x respectively
Then,
$$\eqalign{ & 7x + 4x = \frac{1}{7} \cr & \Rightarrow 11x = \frac{1}{7} \cr & \Rightarrow x = \frac{1}{{77}} \cr & \therefore {\text{A's 1 day's work}} \cr & = \left( {\frac{1}{{77}} \times 7} \right) \cr & = \frac{1}{{11}} \cr} $$
Hence, A alone can do the job in 11 days.
87. A road of 5 m length will be constructed in 100 days. So, 280 workers were employed. But after 80 days it was found that only $${\text{3}}\frac{1}{2}$$ km road was completed. Now how many more people were need to finish the work in the specified time ?
a) 480
b) 80
c) 200
d) 100
Explanation: Let 'n' more number of man are required to complete the job in 20 day.
$$\frac{{{{80}_{{\text{days}}}} \times {\text{28}}{{\text{0}}_{{\text{worker}}}}}}{{{\text{3}}{\text{.5 km}}}} = $$ $$\frac{{{{\left( {{\text{280}} + {\text{n}}} \right)}_{{\text{worker}}}} \times {\text{2}}{{\text{0}}_{{\text{days}}}}}}{{{\text{1}}{\text{.5 km}}}}$$
$$\eqalign{ & {\text{After solving:}} \cr & \Rightarrow 480 = 280 + {\text{n}} \cr & \Rightarrow {\text{n}} = 200 \cr} $$
88. If the work done by (x - 1) men in (x + 1) days and the work done by (x + 2) men in (x - 1) days are in the ratio 9 : 10, then the value of x is equal to ?
a) 5
b) 6
c) 7
d) 8
Explanation: Put values in formula
$$\frac{{{{\left( {x - 1} \right)}_{{\text{men}}}} \times {{\left( {x + 1} \right)}_{{\text{days}}}}}}{{{{\text{9}}_{{\text{work}}}}}} = $$ $$\frac{{{{\left( {x + 2} \right)}_{{\text{men}}}} \times {{\left( {x - 1} \right)}_{{\text{days}}}}}}{{{{10}_{{\text{work}}}}}}$$
$$\eqalign{ & \Rightarrow \frac{{x + 1}}{9} = \frac{{x + 2}}{{10}} \cr & \Rightarrow 10x + 10 = 9x + 18 \cr & \Rightarrow x = 8 \cr} $$
89. A can do a piece of work in 70 days and B is 40% more efficient then A. Then the number of days taken by B to do the same work is = ?
a) 40 dayd
b) 60 days
c) 50 days
d) 45 days
Explanation:
| A | : | B | |
| Efficiency → | 100% | : | 140% |
| 5 | : | 7 | |
| ⤩ | |||
| Time | 7 | : | 5 |
| ×10↓ | ↓×10 | ||
| Actual Time | 70 days | 50 days |
90. A can do a certain work in 12 days. B is 60% more efficient then A. How many days will B and A together take to do the same job?
a) $$\frac{{80}}{{13}}{\text{days}}$$
b) $$\frac{{70}}{{13}}{\text{days}}$$
c) $$\frac{{75}}{{13}}{\text{days}}$$
d) $$\frac{{60}}{{13}}{\text{days}}$$
Explanation: Time taken by B to complete the work
$$\eqalign{ & = 12 \times \frac{{100}}{{160}} \cr & = \frac{{15}}{2}\,{\text{days}} \cr} $$
∴ (A + B)'s 1 day's work
$$\eqalign{ & = \frac{1}{{12}} + \frac{2}{{15}} \cr & = \frac{{5 + 8}}{{60}} \cr & = \frac{{13}}{{60}} \cr} $$
Hence, the work will be completed in $$\frac{{60}}{{13}}$$ days
91. A contractor undertakes to make a road in 40 days and employs 25 men. After 24 days, he finds that only one-third of the road is made. How many extra men should he employ so that he is able to complete the work 4 days earlier ?
a) 100
b) 60
c) 75
d) None of these
Explanation:
$$\eqalign{ & {\text{Let additional men be }}x \cr & \frac{{25 \times 24}}{{{\text{Work}} \to \frac{1}{3}}} = \frac{{\left( {25 + x} \right) \times 12}}{{\frac{2}{3}\left( {{\text{Remaining work 1}} - \frac{1}{3}} \right)}} \cr & \Rightarrow x = 75 \cr} $$
92. 639 persons can repair a road in 12 days working 5 hours a day. In how many days will 30 persons working 6 hours a day complete the work ?
a) 210 days
b) 213 days
c) 214 days
d) 215 days
Explanation:
$$\eqalign{ & {\text{According to the question,}} \cr & {\text{Let, D is number of days}} \cr & \frac{{639 \times 12 \times 5}}{{1{\text{ road}}}} = \frac{{30 \times 6 \times {\text{D}}}}{{1{\text{ road}}}} \cr & \Leftrightarrow {\text{D}} = {\text{213 days}} \cr} $$
93. If 72 men can build a wall of 280 m length in 21 days, how many men could take 18 days to build a similar type of wall of length 100 m ?
a) 30
b) 10
c) 18
d) 28
Explanation:
$$\eqalign{ & {\text{Here work is 280 m length of wall }} \cr & {\text{And 100 m length of wall}} \cr & {\text{Let, M men will finish 100 m wall}}{\text{.}} \cr & \frac{{72 \times 21}}{{280}} = \frac{{{\text{M}} \times {\text{18}}}}{{100}} \cr & \Leftrightarrow {\text{M}} = 30 \cr} $$
94. 4 mat-weavers can weave 4 mats in 4 days. At the same rate how many mats would be woven by 8 mat-weavers in 8 days ?
a) 4
b) 8
c) 12
d) 16
Explanation:
$$\eqalign{ & \frac{{{4_{{\text{mat - wevers}}}} \times {4_{{\text{days}}}}}}{{{4_{{\text{mats}}}}}} = \frac{{{8_{{\text{mat - wevers}}}} \times {8_{{\text{days}}}}}}{{{{\text{N}}_{{\text{mats}}}}}} \cr & \Leftrightarrow {\text{N}} = {\text{16 mats}} \cr} $$
95. A can do a piece of work in 4 hours, B and C together in 3 hours, and A and C together in 2 hours. How long will B alone take to do it ?
a) 8 hours
b) 10 hours
c) 12 hours
d) 24 hours
Explanation:
$$\eqalign{ & {\text{A's 1 hour's work}} = \frac{1}{4} \cr & \left( {{\text{B}} + {\text{C}}} \right){\text{'s 1 hour's work}} = \frac{1}{3} \cr & \left( {{\text{A}} + {\text{C}}} \right){\text{'s 1 hour's work}} = \frac{1}{2} \cr & \left( {{\text{A}} + {\text{B}} + {\text{C}}} \right){\text{'s 1 hour's work}} \cr & = \frac{1}{4} + \frac{1}{3} \cr & = \frac{7}{{12}} \cr & \therefore {\text{B's 1 hour's work}} \cr} $$
= (A + B + C)'s 1 hour's work - (A + C)'s 1 hour's work
$$\eqalign{ & = \frac{7}{{12}} - \frac{1}{2} \cr & = \frac{1}{{12}} \cr} $$
So, B alone can complete the work in 12 hours.
96. A 10 hectare field is reaped by 2 men, 3 women and 4 children together in 10 days. If working capabilities of a man, a woman and a child are in the ratio 5 : 4 : 2, then a 16 hectare field will be reaped by 6 men, 4 women and 7 children in = ?
a) 5 days
b) 6 days
c) 7 days
d) 8 days
Explanation: According to the question,
Efficiency of a man, a woman and a child are
$$\eqalign{ & 5:4:2{\text{ units/day}} \cr & {\text{One day work of 2 men}} \cr & = 2 \times 5 \cr & = 10{\text{ units}} \cr & {\text{One day work of 3 women}} \cr & = 3 \times 4 \cr & = 12{\text{ units}} \cr & {\text{One day work of 4 children}} \cr & = 4 \times 2 \cr & = 8{\text{ units}} \cr} $$
Applying formula, let time taken is D days.
$$\frac{{\left( {10 + 12 + 8} \right) \times {{10}_{{\text{days}}}}}}{{{{10}_{{\text{hectare}}}}}} = $$ $$\left[ {\frac{{\left( {{6_{{\text{men}}}} \times 5} \right) + \left( {{4_{{\text{women}}}} \times 4} \right) + \left( {{7_{{\text{children}}}} \times 2} \right) \times {\text{D}}}}{{{{16}_{{\text{hectare}}}}}}} \right]$$
$$\eqalign{ & \Leftrightarrow \frac{{\left( {30} \right) \times 10}}{{10}} = \frac{{\left[ {60} \right] \times {\text{D}}}}{{16}} \cr & \Leftrightarrow {\text{D}} = 8{\text{ days}} \cr} $$
97. If p men working p hours per day for p days produce p units of work, then the units of work produced by n men working n hours a day for days is = ?
a) $$\frac{{{{\text{p}}^{\text{2}}}}}{{{{\text{n}}^{\text{2}}}}}$$
b) $$\frac{{{{\text{p}}^{\text{3}}}}}{{{{\text{n}}^{\text{2}}}}}$$
c) $$\frac{{{{\text{n}}^{\text{2}}}}}{{{{\text{p}}^{\text{2}}}}}$$
d) $$\frac{{{{\text{n}}^{\text{3}}}}}{{{{\text{p}}^{\text{2}}}}}$$
Explanation: Applying formula
Let work done by 'n' men and women
$$\frac{{{{\text{p}}_{{\text{men}}}} \times {{\text{p}}_{{\text{hours}}}} \times {{\text{p}}_{{\text{days}}}}}}{{{{\text{p}}_{{\text{units}}}}}} = $$ $$\frac{{{{\text{n}}_{{\text{men}}}} \times {{\text{n}}_{{\text{hours}}}} \times {{\text{n}}_{{\text{days}}}}}}{{{{\text{W}}_{{\text{units}}}}}}$$
$$\eqalign{ & \Leftrightarrow {{\text{p}}^{\text{2}}} = \frac{{{{\text{n}}^{\text{3}}}}}{{\text{w}}} \cr & \Leftrightarrow {\text{W}} = \frac{{{{\text{n}}^{\text{3}}}}}{{{{\text{p}}^{\text{2}}}}} \cr} $$
98. If two persons, with equal abilities, can do two jobs in two days then 100 persons with equal abilities can do 100 similar jobs in = ?
a) 100 days
b) 10 days
c) 5 days
d) 2 days
Explanation:
$$\frac{{{{\text{2}}_{{\text{person}}}} \times {{\text{2}}_{{\text{days}}}}}}{{{{\text{2}}_{{\text{jobs}}}}}} = \frac{{{\text{100}} \times {\text{D}}}}{{{\text{10}}{{\text{0}}_{{\text{jobs}}}}}}$$ (D is number of days required)
$$\eqalign{ & {\text{After solving}} \cr & {\text{D}} = 2{\text{ days}} \cr} $$
99. A is twice as good a workman as B. If they work together, they can complete a job in 18 days. If A alone does the job, in how many days he will complete the job ?
a) 27 days
b) 36 days
c) 40 days
d) 54 days
Explanation: (A's 1 day's work) : (B's 1 day's work)
$$\eqalign{ & = 2:1 \cr & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} = \frac{1}{{18}} \cr & \therefore {\text{A's 1 day's work}} \cr & = \left( {\frac{1}{{18}} \times \frac{2}{3}} \right) \cr & = \frac{1}{{27}} \cr} $$
Hence, A alone can finish the work in 27 days
100. A is thrice as good a workman as B and so takes 60 days less than B for doing a job. The time in which they can do the job together is = ?
a) $$22\frac{1}{2}\,{\text{days}}$$
b) $${\text{30 days}}$$
c) $${\text{45 days}}$$
d) $${\text{60 days}}$$
Explanation: Ratio of times taken by A and B = 1 : 3
If difference of time is 2 days, B takes 3 days
If difference of time is 60 days, B takes
$$\eqalign{ & = \left( {\frac{3}{2} \times 60} \right) \cr & = {\text{90 days}} \cr} $$
So, A takes 30 days to do the work
$$\eqalign{ & {\text{A's 1 day's work}} = \frac{1}{{30}} \cr & {\text{B's 1 day's work}} = \frac{1}{{90}} \cr & \left( {{\text{A}} + {\text{B}}} \right){\text{'s 1 day's work}} \cr & = \left( {\frac{1}{{30}} + \frac{1}{{90}}} \right) \cr & = \frac{4}{{90}} \cr & = \frac{2}{{45}} \cr} $$
∴ A and B together can do the job in
$$\eqalign{ & = \frac{{45}}{2} \cr & = 22\frac{1}{2}\,{\text{days}} \cr} $$