1. If the numerator of a fraction is increased by 20% and the denominator is decreased by 5%, the value of the new fraction becomes $$\frac{5}{2}$$. The original fraction is :
a) $$\frac{24}{19}$$
b) $$\frac{3}{18}$$
c) $$\frac{95}{48}$$
d) $$\frac{48}{95}$$
Explanation: Let the fraction = $$\frac{x}{y}$$
According to the question,
$$\frac{x × 120}{y × 95}$$ = $$\frac{5}{2}$$
$$\frac{x}{y}$$ = $$\frac{5 × 95}{2 × 120}$$
$$\frac{x}{y}$$ = $$\frac{95}{48}$$
2. A line of length 1.5 metres was measured as 1.55 metres by mistakes. What will be the value of error percent ?
a) 0.05%
b) $$3\frac{7}{31}$$%
c) $$3\frac{1}{3}$$%
d) 0.08%
Explanain: Percentage error :
= $$\frac{1.55 - 1.50}{1.50}$$ × 100
= $$\frac{0.05}{1.50}$$ × 100
= $$\frac{5}{150}$$ × 100
= $$\frac{5 × 2}{3}$$
= $$\frac{10}{3}$$
= $$3\frac{1}{3}$$%
3. A reduction of 20% in the price of wheat enables Bhuvnesh to buy 5 kg more wheat for Rs. 320. The original rate (in rupees per kg) of wheat was :
a) 16
b) 18
c) 20
d) 21
Explanation: Let the initial expenditure = 100 units
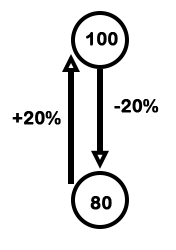
Increase in consumption
= $$\frac{20}{80}$$ = $$\frac{1}{4}$$
1 unit = 5 kg
Original consumption
= 5 × 4 = 20 kg
New consumption
= 5 × 5 = 25 kg
Original price = $$\frac{320}{20}$$ = 16 per kg
4. If the height of a cylinder is increased by 15% and the radius of its base is decreased by 10% then the percentage change in its curved surface area is :
a) 2.5% increased
b) 3.5% increased
c) 2.5% decreased
d) 3.5% decreased
Explanation: Increase in height = 15% = $$\frac{3}{20}$$
Decrease in base radius = 10% = $$\frac{1}{10}$$
| Initial | Final | |
| Radius | 10 | 9 |
| height | 20 | 23 |
| Area | 200 | 207 |
Increment in Area = 207 - 200 = 7
Required % increase in area
= $$\frac{7}{200}$$ × 100
= 3.5%
5. Two numbers are respectively 20% and 50% of the third number. What percent is the first number of the second ?
a) 10%
b) 20%
c) 30%
d) 40%
Explanation: Let the 3rd number is 100
According to the question,
$$\eqalign{ & \,{1^{{\text{st}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{2^{{\text{nd}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{3^{{\text{rd}}}} \cr & 20\,\,\,\,\,\,\,:\,\,\,\,\,\,\,\,50\,\,\,\,\,\,\,\,:\,\,\,\,\,\,\,100 \cr} $$
Required % = $$\frac{20}{50}$$ × 100 = 40%
6. In an examination, 65% of the students passed in Mathematics, 48% passed in Physics and 30% passed in both. How much percent of students failed in both the subjects ?
a) 17%
b) 43%
c) 13%
d) 47%
Explanation: Pass students in Mathematics = 65%
Pass students in Physics = 48%
Student pass in both subject Mathematics and Physics = 30%
Student only pass in Mathematics = 65 - 30 = 35%
Student only pass in Physics = 48 - 30 = 18%
Percentage of Failed students in both subjects :
= 100 - [ student pass only in Mathematics + student pass only in Physics + student pass in both subject]
= [100 - (35 + 18 + 30)]
= 17%
7. At an election there were two candidate got 38% of votes and lost by 7200 votes. The total numbers of valid votes were :
a) 13000
b) 13800
c) 16200
d) 30000
Explanation: Let the total number of votes = 100x
losser candidate get 38% of vote i.e. = 38x and winner will get = 100x - 38x = 62x
According to the question,
62x - 38x = 7200
⇒ 24x = 7200
⇒ x = 300
Total votes = 100x
= 100 × 300
= 30000
8. In 2 kg mixture of copper and aluminium, 30% is copper. How much aluminium powder should be added to the mixture so that the quantity of copper becomes 20% ?
a) 900 gms
b) 800 gms
c) 1000 gms
d) 1200 gms
Explanation: According to the question,
Mixture of copper and aluminium = 2000 gms
30% copper = $$\frac{30}{100}$$ × 2000 = 600 gms
Aluminium in mixture = 2000 - 600 = 1400gm
Now 'x' weight of mixture have and 600 gm copper become 20% of its total weight.
i.e. x = $$\frac{{600}}{{20}} \times 100 $$ = 3000gm
Total amount of Aluminium in mixture = 3000 - 600 = 2400
Additional aluminium powder added = 2400 - 1400 = 1000gm
9. If 20% of (A + B) = 50% of B, then value of $$\frac{2A - B}{2A + B}$$ is :
a) $$\frac{1}{2}$$
b) $$\frac{1}{3}$$
c) $$\frac{1}{41}$$
d) 1
Explanation:
$$\frac{20}{100}$$ (A + B) = $$\frac{50}{100}$$ (B)
2A + 2B = 5B
2A = 3B
A = $$\frac{3}{2}$$ put value of A in given equation
$$\frac{2A - B}{2A + B}$$
= $$\frac{3B - B}{3B + B}$$
= $$\frac{2B}{4B}$$
= $$\frac{1}{2}$$
10. Ticket for all but 100 seats in a 10000 seat stadium were sold. Of the ticket sold, 20% were sold at half price and the remaining tickets were sold at the full price of Rs. 20. The total revenue from the ticket sales, (in Rs.) was :
a) 158400
b) 178200
c) 180000
d) 198000
Explanation: Total seats = 10000
Ticket sold = (10000 - 100) = 9900
According to the question,
Total revenue
= 9900 × $$\frac{20}{100}$$ × 10 + 9900 × $$\frac{80}{100}$$ × 20
= 9900 × 2 + 9900 × 16
= 9900 (2 + 16)
= Rs. 178200
11. An army lost 10% of its men in war. 10% of the remaining died due to disease and 10% of the rest were declared disabled. Thus the strength of the army was reduced to 729000 active men. The original strength of the army was :
a) 1500000
b) 1000000
c) 1200000
d) 1100000
Explanation: Initial number of soldiers in the army = x
According to the question,
$$\eqalign{ & \Rightarrow {\text{x}} \times \frac{{90}}{{100}} \times \frac{{90}}{{100}} \times \frac{{90}}{{100}} = 729000 \cr & \Rightarrow x = \frac{{729000 \times 1000}}{{9 \times 9 \times 9}} \cr & \Rightarrow x = 1000000 \cr} $$
12. In an examination, 35% of total students failed in Hindi, 45% failed in English and 20% failed in both. Find the percentage of those students who passed in both the subjects ?
a) 45%
b) 35%
c) 20%
d) 40%
Explanain : Failed students in Hindi = 35%
Failed students in English = 45%
Student failed in both subject hindi and english = 20%
Student only fail in hind = 35 - 20 = 15%
Student only fail in English = 45 - 20 = 25%
Percentage of passed students in both subjects :
= 100 - [ student fail in hindi + student fail in english + student fail in both subject]
= [100 - (15 + 25 + 20)]
= 40%
13. The price of an article was increased by r%. Later the new price was decreased by r%. If the latest price was Rs. 1, then the original price was :
a) Rs. 1
b) Rs. $$\frac{{1 - {r^2}}}{{100}}$$
c) Rs. $$\frac{{\sqrt {1 - {r^2}} }}{{100}}$$
d) Rs. $$\left( {\frac{{10000}}{{10000 - {r^2}}}} \right)$$
Explanation: r% = $$\frac{r}{100}$$
| Initial Price | Final | |
| 100 | (100 + r) | |
| 100 | (100 - r) | |
| 10000 | (100 + r) (100 - r) |
According to the question,
(100 + r) (100 - r) units = Rs. 1
(10000 - r2) units = Rs. 1
1 unit = $$\left( {\frac{{1}}{{10000 - {r^2}}}} \right)$$
Original price = $$\left( {\frac{{10000}}{{10000 - {r^2}}}} \right)$$
14. The difference of two numbers is 15% of larger sum. The ratio of the larger number to the smaller number is :
a) 23 : 17
b) 11 : 9
c) 17 : 11
d) 23 : 11
Explanation: Let the number are a and b
where a > b
According to the question,
(a - b) = $$\frac{15}{100}$$ (a + b)
(a - b) = $$\frac{3}{20}$$ (a + b)
20a - 20b = 3a + 3b
17a = 23b
$$\frac{a}{b}$$ = $$\frac{23}{17}$$
Required ratio = 23 : 17
15. A number if reduced by 25% becomes 225. By what percent should it be increased so that it becomes 375 ?
a) 25%
b) 30%
c) 35%
d) 75%
Explanation: Let the number = x
According to the question,
$$\frac{x × (100 - 25)}{100}$$ = 225
x = $$\frac{225 × 100}{75}$$
x = 300
Required percentage :
= $$\frac{(375 - 300)}{300}$$ × 100
= 25%
16. 2 is what percent of 50 ?
a) 2%
b) 2.5%
c) 4%
d) 5%
Explanation: Required % = $$\frac{2}{50}$$ × 100 = 4%
17. 15% of 45% of a number is 105.3. What is 24% of that number.
a) 385.5
b) 374.4
c) 390
d) 375
Explanation: Let the number be x
⇒ x × $$\frac{15}{100}$$ × $$\frac{45}{100}$$ = 105.3
⇒ x = 1560
⇒ Required answer
= $$\frac{24}{100}$$ × 1560
= 374.4
18. The ratio 5 : 4 expressed as a percent equals :
a) 125%
b) 405%
c) 80%
d) 12.5%
Explanation: Required % = $$\frac{5}{4}$$ × 100 = 125%
Always writes a : b in % ⇒ $$\frac{a}{b}$$ × 100
19. If 60% of A = $$\frac{3}{4}$$ of B, then A : B is :
a) 9 : 20
b) 20 : 9
c) 4 : 5
d) 5 : 4
Explanation: 60% of A = $$\frac{3}{4}$$B
$$\frac{3}{5}$$A = $$\frac{3}{4}$$B
$$\frac{A}{B}$$ = $$\frac{5}{4}$$
⇒ A : B = 5 : 4
20. In an examination, 93% of students passed and 259 failed. The total number of students appearing at the examination was :
a) 3700
b) 3850
c) 3950
d) 4200
Explanation: Percentage of failed students
= (100 - 93)% = 7%
According to the question,
7% → 259
1% → 37
100% → 3700
Total students = 3700
21. The average of marks obtained by 100 candidates in a certain examination is 30. If the average marks of passed candidates is 35 and that of the failed candidates is 10, what is the number of candidates who passed the examinations ?
a) 60
b) 70
c) 80
d) 90
Explanation: By mixture and allegation method.
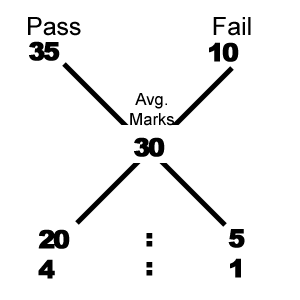
4 : 1 = 5 units
5 units = 100
1 unit = 20
Pass candidate :
= 4 units
= 4 × 20
= 80
22. If 90% of A = 30% of B and B = 2x% of A, then the value of x is :
a) 450
b) 400
c) 300
d) 150
Explanain : 90% of A = 30% of B
90A = 30B
⇒ B = 3A ..... (i)
B = $$\frac{2x}{100}$$ × A
3A = $$\frac{2x}{100}$$ × A
⇒ x = 150
23. 18% of which number is equal to 12% of 75 ?
a) 50
b) 100
c) 2
d) $$\frac{3}{2}$$
Explanation: Let the number = x
According to the question,
⇒ x × $$\frac{18}{100}$$ = $$\frac{12}{100}$$ × 75
⇒ 18x = 12 × 75
⇒ x = $$\frac{12 × 75}{18}$$
⇒ x = 50
Hence, required number = 50
24. Out of his total income, Mr. Kapur spends 20% on house rent and 70% of the rest on house hold expenses. If he saves Rs. 1800 what is his total income (in Rs.) ?
a) Rs. 7800
b) Rs. 7000
c) Rs. 8000
d) Rs. 7500
Explanation: Let Mr.kapur income is 100x
House rent 20%, i.e. 20x
Remaining income 100x - 20x = 80x
Now 70% of his remaining income spend in house hold expenses
i.e. 70% of 80x = 56x
Remain saving is 80x - 56x = 24x
According to question
24x = 1800
x = $$\frac{{1800}}{{24}} = 75$$
Mr.kapur income = 100 × 75 = 7500
25. Two numbers are in the ratio 2 : 3. If 20% of the smaller number added to 20, is equal to the sum of 10% of the larger number and 25, the the smaller number is :
a) 100
b) 160
c) 180
d) 200
Explanation: Let the numbers are 2x and 3x respectively
According to the question,
2x × $$\frac{20}{100}$$ + 20 = 3x × $$\frac{10}{100}$$ + 25
$$\frac{2}{5}$$x + 20 = $$\frac{3}{10}$$ + 25
$$\frac{3}{10}$$x - $$\frac{2}{5}$$x = - 5
3x - 4x = - 50
x = 50
Hence, required smaller number
= 2x
= 2 × 50
= 100
26. Two persons contested an election of Parliament. The winning candidate secured 57% of the total votes polled and won by a majority of 42000 votes. The number of total votes polled is :
a) 500000
b) 600000
c) 300000
d) 400000
Explanation: Let the total number of votes = 100x
Winner candidate get 57% of vote i.e. = 57x and losser will get = 100x - 57x = 43x
According to the question,
57x - 43x = 42000
⇒ 14x = 42000
⇒ x = 3000
Total votes = 100x
= 100 × 3000
= 300000
27. In a factory 60% of the workers are above 30 years and of these 75% are male and the rest are females. If there are 1350 male workers above 30 years, the total number of workers in the factory is :
a) 3000
b) 2000
c) 1800
d) 1500
Explanation: Given,
60% of work whose age is 30 above
1350 males work whose age is 30 above.
75% of workers are male whose age are 30 above.
25% of female workers whose ages are 30 above.
Number of female work whoes age 30 above
= $$\frac{{1350}}{{75}} \times 25 = 450$$
total number of work whoes age are 30 above = 1350 + 450 = 1800(60% of the work)
Total number of work = $$\frac{{1800}}{{60}} \times 100 = 3000$$
28. In the last financial year, a car company sold 41800 cars. In this year, the target is sale 51300 cars. By what percent must the sale be increased ?
a) $$11\frac{9}{22}$$%
b) $$8\frac{9}{22}$$%
c) $$8\frac{11}{23}$$%
d) $$22\frac{8}{11}$$%
Explanation: Percentage increase :
= $$\frac{51300 - 41800}{41800}$$ × 100
= $$\frac{9500}{41800}$$ × 100
= $$\frac{9500}{418}$$
= $$\frac{500}{22}$$
= $$\frac{250}{11}$$
= $$22\frac{8}{11}$$%
29. One third of a number is 96. What will 67% of that number be ?
a) 192.96
b) 181.44
c) 169.92
d) 204.48
Explanation: Let the number = x
⇒ $$\frac{1}{3}$$ × x = 96
⇒ x = 288
⇒ Required answer :
= $$\frac{67}{100}$$ × 288
= 192.96
30. If the duty on an article is reduced by 40% of his present rate by how much percent must its consumption increase in order that the revenue remains unaltered ?
a) 60%
b) $$62\frac{1}{3}$$%
c) 72%
d) $$66\frac{2}{3}$$%
Explanation:% change = $$\frac{{\text{R}}}{{100 \pm {\text{R}}}}$$ × 100%
Required answer :
= $$\frac{40}{100 - 40}$$ × 100
= $$\frac{40}{60}$$ × 100
= $$\frac{200}{3}$$
= $$66\frac{2}{3}$$%
31. When 75 added to 75% of a number, the answer is the number. Find 40% of that number.
a) 100
b) 80
c) 120
d) 160
Explanation: 75% = $$\frac{3}{4}$$
Let the number = 4x
According to the question,
4x × $$\frac{3}{4}$$ + 75 = 4x
x = 75
Number = 75 × 4 = 300
Required answer :
= 300 × $$\frac{40}{100}$$
= 120
32. If 15% of (A + B) = 25% of (A - B), then what percent of B equal to A ?
a) 10%
b) 60%
c) 200%
d) 400%
Explanain:
$$\frac{15}{100}$$ (A + B) = $$\frac{25}{100}$$ (A - B)
⇒ 15A + 15B = 25A - 25B
⇒ 10A = 40B
⇒ A = 4B
Required % :
= $$\frac{A}{B}$$ × 100
= $$\frac{4B}{B}$$ × 100
= 400%
33. When 60 is subtracted from 60% of a number, the result is 60. The number is :
a) 120
b) 150
c) 180
d) 200
Explanation: Note : In percentage always assume data. Which make your Calculation easier.
60% $$\frac{3}{5}$$
Let the number = 5x
Accounting to the question,
⇒ 5x × $$\frac{3}{5}$$ - 60 = 60
⇒ x = $$\frac{120}{3}$$
⇒ x = 40
Hence, required number :
= 5x
= 5 × 40
= 200
34. In an examination A got 25% marks more than B, B got 10% less than C and C got 25% more than D. If D got 320 marks out of 500, the marks obtained by A were :
a) 405
b) 450
c) 360
d) 400
Explanation: Marks obtained by D = 320
Marks obtained by C
= 320 × $$\frac{125}{100}$$ = 400
Marks obtained by B
= 400 × $$\frac{(100 - 10)}{100}$$ = 360
Marks obtained by A
= 360 × $$\frac{125}{100}$$ = 450
Hence, required marks obtained by A = 450
35. A reduction of 10% in the price of an apple enable a man to buy 10 apples more for Rs. 54. The reduced price of apples per dozen is :
a) Rs. 6.48
b) Rs. 12.96
c) Rs. 10.80
d) Rs. 14.40
Explanation: Let initial expenditure = 100 units
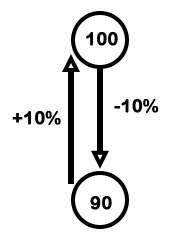
Required increment = $$\frac{10}{90}$$ = $$\frac{1}{9}$$
1 unit = 10 apples
Original consumption = 9 units
= 9 × 10 = 90 apples
New consumption = 10 units
= 10 × 10 = 100 apples
New price = $$\frac{54}{100}$$ × 12 = Rs. 6.48 per dozen
36. If X is 20% less then Y, then find the value of $$\frac{Y - X}{Y}$$ and $$\frac{X}{X - Y}$$ :
a) $$\frac{1}{5}$$, - 4
b) 5, $$\frac{1}{4}$$
c) $$\frac{2}{5}$$, $$-\frac{5}{2}$$
d) $$\frac{3}{5}$$, $$-\frac{3}{5}$$
Explanation: 20% = $$\frac{1}{5}$$ = $$\frac{4}{5}$$
X : Y
4 : 5
Let X = 4a
Y = 5a
Hence,
⇔ $$\frac{Y - X}{Y}$$
= $$\frac{5a - 4a}{5a}$$
= $$\frac{a}{5a}$$
= $$\frac{1}{5}$$
⇔ $$\frac{X}{X - Y}$$
= $$\frac{4a}{4a - 5a}$$
= $$\frac{4a}{- a}$$
= - 4
Hence required answer = $$\frac{1}{5}$$, - 4
37. The ratio of the number of boys to that of girls in a school is 4 : 1. If 75% of boys and 70% of the girls are scholarship holders, then the percentage of students who do not get scholarship is :
a) 50%
b) 28%
c) 75%
d) 26%
Explanation: Let the number of boys = 400
Let the number of girls = 100
Total number of students who do not get scholarship
= 400 × $$\frac{25}{100}$$ + 100 × $$\frac{30}{100}$$
= 100 + 30
= 130
Required percentage
= $$\frac{130}{500}$$ × 100
= 26%
38. A man had a certain amount with him. He spent 20% of that to buy any article and 5% of the remaining on transport. Then he gifted Rs. 120. If he is left with Rs. 1400, the amount he spent on transport is :
a) Rs. 76
b) Rs. 61
c) Rs. 95
d) Rs. 80
Explanation: Let the total amount = x
According to the question,
x × $$\frac{80}{100}$$ × $$\frac{95}{100}$$ = (120 + 1400)
x × $$\frac{4}{5}$$ × $$\frac{19}{20}$$ = 1520
x = $$\frac{1520 × 100}{76}$$
x = 2000
Total amount = 2000
Amount spent on transport
= 2000 × $$\frac{80}{100}$$ × $$\frac{5}{100}$$
= Rs. 80
39. The income of a company increases 20% per annum. If its income is Rs. 2664000 in the year 2012. Then its income in the year 2010 was :
a) Rs. 2120000
b) Rs. 1850000
c) Rs. 2820000
d) Rs. 2855000
Explanation: Let the income in 2010 be P
⇒ R = 20%
⇒ Income of year 2012
⇒ Rs. 2664000
$$\eqalign{ & \Rightarrow {\text{Income of 2012}} = P{\left[ {1 + \frac{R}{{100}}} \right]^2} \cr & \Rightarrow 2664000 = P{\left[ {1 + \frac{{20}}{{100}}} \right]^2} \cr & \Rightarrow 2664000 = P \times \frac{6}{5} \times \frac{6}{5} \cr & \Rightarrow {\text{Income in 2010 = 1850000}} \cr} $$
40. An individual pays 30% income tax. On this he has to pay a surcharge of 10%. Thus, the net tax rate, he has pay is :
a) 45%
b) 40%
c) 33%
d) 27%
Explanation: Net tax rate
= 30 + $$\frac{30 × 10}{100}$$
= 33%
41. The difference between the value of the number increased by 20% and the value of the number decreased by 25% is 36. Find the number ?
a) 7.2
b) 0.2
c) 720
d) 80
Explanation: Let the number = x
According to the question,
⇒ x × $$\frac{120}{100}$$ - x × $$\frac{75}{100}$$ = 36
⇒ 120x - 75x = 3600
⇒ 45x = 3600
⇒ x = $$\frac{3600}{45}$$
⇒ x = 80
Hence, required number = 80
42. In a village, each of the 60% of families has a cow; each of the 30% of families has a buffalo and each of the 15% of families has both a cow and buffalo. In all there are 96 families in the village. How many families do not have a cow or a buffalo ?
a) 20
b) 24
c) 26
d) 28
Explanain: 15% of families have cow and buffalo.
Families only have cow = 60 - 15 = 45%
Families only have buffalo = 30 - 15 = 15%
Required families which do not have a cow or a buffalo
= 100 - (Families only have cow + Families only have buffalo + Families have cow and buffalo)
= 100 - (45 + 15 + 15)
= 25%
According to the question,
Required number
= $$\frac{96}{100}$$ × 25
= 24
43. The population of a village has increased annually at the rate of 25%. If at the end of 3 years it is 10000, the population in the beginning of the first year was :
a) 5120
b) 5000
c) 4900
d) 4500
Explanation: 25% = $$\frac{1}{4}$$
\[\begin{gathered} {\text{Initial }}\,\,\,\,\,\,{\text{Final}} \hfill \\ \,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5 \hfill \\ \,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5 \hfill \\ \,\,\,4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,5 \hfill \\ \overline {\,\,\,\,\,\,64\,\,\,\,\,\,\,\,\,\,125\,\,\,} \hfill \\ \end{gathered} \]
⇒ 125 units = 10000
⇒ 1 unit = 80
⇒ 64 units = 5120
⇒ Population at the beginning of 1st year = 5120
44. A saves 20% of his monthly salary. If his monthly expenditure is Rs. 6000, then his monthly savings is :
a)Rs. 1500
b) Rs. 1800
c) Rs. 1200
d) Rs. 4800
Explanation: Let the salary = 100 units
Savings = 20%
Savings = 100 × $$\frac{20}{100}$$ = 20 units
Expenditure = (100 - 20) = 80 units
According to the question,
80 units = Rs. 6000
1 unit = Rs. 75
Savings = 75 × 20 = Rs. 1500
45. A man spends 75% of his income. His income increased by 20% and he increased his expenditure by 15%. His savings will then be increased by :
a) 33%
b) $$33\frac{1}{3}$$%
c) 35%
d) 40%
Explanation: Let the income of the man = Rs. 100
∴Intial Expenditure = Rs.75
Now new income become = 100 + 20% of 100 = Rs. 120
New Expenditure = 75 + 15% of 75 = Rs.86.25
Intial Saving = 100 - 75 = Rs. 25
New Saving = 120 - 86.25 = Rs. 33.75
Required percentage increase :
= $$\frac{(33.75 - 25)}{25}$$ × 100
= 35%
46. The sum of two numbers is 520. If the bigger number is decreased by 4% and the smaller number is increased by 12% then the numbers obtained are equal. The smaller number is :
a) 280
b) 240
c) 210
d) 300
Explanation: Let the bigger number is a and the smaller number is (520 - a)
According to the question,
a × $$\frac{(100 - 4)}{100}$$ = (520 - a) × $$\frac{(100 + 12)}{100}$$
$$\frac{96a}{100}$$ = (520 - a) $$\frac{112}{100}$$
96a = (520 - a) 112
13a = 3640
a = 280
Hence, bigger number = 280
Smaller number = (520 - 280) = 240
47. Tulsiram's salary is 20% more then that of Kashyap. If Tulsiram saves Rs. 720 which is 4% of his salary, then Kashyap's salary is :
a) Rs. 15000
b) Rs. 12000
c) Rs. 10000
d) Rs. 22000
Explanation: Salary of Tulsiram
= Rs. $$\frac{720}{4}$$ × 100
= Rs. 18000
Salary of Kashyap
= 18000 × $$\frac{100}{120}$$
= Rs. 15000
48. The ratio of the number of boys to that of girls in a village is 3 : 2. If 30% of boys and 70% of girls appeared in an examination, the ratio of the number of students, appeared in the examination to that not appeared in the same examination is :
a) 1 : 1
b) 27 : 23
c) 9 : 14
d) 23 : 27
Explanation: According to the question,
Let the total number of students = 100
Ratio of Boys and Girls =$$\frac{3}{2}$$
Total number of Boy = $$\frac{3}{5} \times 100 = 60$$
Total number of Girl = $$\frac{2}{5} \times 100 = 40$$
30% of boy appeared in exam = 30% of 60 = 18
70% of girl appeared in exam = 70% of 40 = 28
Total number of student appeared in exam = 18 + 28 = 46
Students not appeared in exam = 100 - 46 = 54
$$\therefore \frac{{{\text{Ratio of students appeared in exam}}}}{{{\text{Not appeared in exam}}}}$$
= $$\frac{46}{54}$$
= $$\frac{23}{27}$$
= 23 : 27
49. The value of a machine is Rs. 6250. It decreases by 10% during the first year, 20% during the second year and 30% during the third year, What will be the value of the machine after 3 years ?
a) Rs. 2650
b) Rs. 3050
c) Rs. 3150
d) Rs. 3550
Explanation: Current value of machine
$$\eqalign{ & = 6250 \times \frac{{90}}{{100}} \times \frac{{80}}{{100}} \times \frac{{70}}{{100}} \cr & = {\text{Rs}}{\text{. 3150}} \cr} $$
50. A person gave 20% of his income to his elder son, 30% of remaining to the younger son and 10% of the balance, he donate to a trust. He is left with Rs. 10080. His income was :
a) Rs. 50000
b) Rs. 40000
c) Rs. 30000
d) Rs. 20000
Explanation: Let Person income is 100x
20% his income give to elder son, i.e. 20x
Remaining income 100x -20x = 80x
Now 30% of his remaining income given to his younger son
i.e. 30% of 80x = 24x
Remain saving is 80x - 24x = 56x
Now 10% of his remaining income he donated to a trust
i.e. 10% of 56x = 5.6x
Remain income = 56x - 5.6x = 50.4x
According to question
50.4x = 10080
x = $$\frac{{10080}}{{50.4}}$$ = 200
Person income = 100 x 200 = Rs. 20000
51. 25% of the candidates who appeared in an examination failed and only 450 students qualify the exam. The number of students who appeared in the examination was :
a) 700
b) 600
c) 550
d) 500
Explanation: Percentage of failed students = 25%
∴ Percentage of passed students
= (100 - 25)% = 75%
According to the question,
Total students :
= $$\frac{450}{75}$$ × 100 = 600
52. In an assembly election, a candidate got 55% of the total valid votes. 2% of the total votes were declared invalid. If the total number of voters is 104000, then the number of valid votes polled in favour of the candidate is :
a) 56506
b) 56650
c) 56560
d) 56056
Explanain: Total votes = 104000
Total valid votes :
= 104000 × $$\frac{(100 - 2)}{100}$$
= 104000 ×$$\frac{98}{100}$$
= 101920
Votes polled in favour of the candidate :
= 101920 × $$\frac{55}{100}$$
= 56056
53. 75 gm of sugar solution has 30% sugar in it. Then the quantity of sugar that should be added to the solution to make the quantity of the sugar 70% in the solution is :
a) 125 gm
b) 100 gm
c) 120 gm
d) 130 gm
Explanation: Sugar in original solution = $$\frac{{75 \times 30}}{{100}}$$ = 22.5 gm
Let m gm of sugar be mixed.
$$\therefore \frac{{22.5 + {\text{m}}}}{{75 + {\text{m}}}} \times 100 = 70$$
⇒ 2250+ 100m = 75 × 70 + 70m
⇒ 2250 + 100m = 5250 + 70m
⇒ 30m = 5250 - 2250 = 3000
⇒ m = $$\frac{{3000}}{{30}}$$ = 100 gm
54. In an examination, 1100 boys and 900 girls appeared, 50% of the boys and 40% of the girls passed the examination. The percentage of candidates who failed :
a) 45%
b) 45.5%
c) 50%
d) 54.5%
Explanation:Total number boy = 1100 and girl = 900
Total number of boy fail (50%) = 550
Total number of girl fail ( 60%) = 540
Total failed candidates = (550 + 540) = 1090
Required percentage of failed candidates :
= $$\frac{1090}{(1100 + 900)}$$ × 100
= $$\frac{1080 × 100}{2000}$$
= 54.5%
55. Christy donated 10% of his income to an orphanage and deposited 20% of the remainder in his bank. If he has now Rs. 7200 left, what is his income :
a) Rs. 10000
b) Rs. 8000
c) Rs. 9000
d) Rs. 8500
Explanation: Total income = 100x
10% deposit to orphange = 100x of 10% = 10x
Remain income 90x
Now 20% deposit to bank = 90x of 20% = 18x
Reamin income 90x - 18x = 72x
According to question
72x = 7200
⇒ x = $$\frac{7200}{72}$$ = 100
Income of Christy = 100 × 100 = 10000
56. The percentage of metals in a mine of lead ore is 60%. Now the percentage of silver is $$\frac{3}{4}$$% of metals and the rest is lead. If the mass of ore extracted from this mine is 8000 kg, the mass (in kg.) of lead is :
a) 4763
b) 4764
c) 4762
d) 4761
Explanation: Mass of lead ore = 8000 kg
⇒ Mass of metal in lead ore
= 60% of 8000
= 4800 kg
⇒ Mass of silver in metal
= $$\frac{3}{4}$$% of 4800
= 36 kg
⇒ Mass of lead in ore
= 4800 - 36
= 4764 kg
57. If 120 is 20% of a number, then 120% of that number will be :
a) 20
b) 120
c) 480
d) 720
Explanation: Let the number = x
According to the question,
x × $$\frac{20}{100}$$ = 120
x = 600
Required answer
= 600 × $$\frac{120}{100}$$ = 720
58. 498 is 17% less than a number then the number is :
a) 610
b) 580
c) 600
d) 620
Explanation: Let the number = x
According to the question,
⇒ x - $$\frac{17x}{100}$$ = 498
⇒ 100x - 17x = 49800
⇒ 83x = 49800
⇒ x = $$\frac{49800}{83}$$ = 600
59. If radius of a circle is increased by 5%, then the increase in it's area is :
a) 10.25%
b) 5.75%
c) 10%
d) 5%
Explanation: Quicker approach
$$ \uparrow $$ in A = a + b + $$\frac{ab}{100}$$
Here a = b = 5%
$$ \uparrow $$ in A :
$$\eqalign{ & = \left( {5 + 5 + \frac{{5 \times 5}}{{100}}} \right)\% \cr & = 10.25\% \cr} $$
60. If 60% of A's income is equal to 75% of B's income, then B's income is equal to x% of A's income. The value of x is :
a) 70
b) 60
c) 80
d) 90
Explanation: According to the question,
⇒ 60 × $$\frac{A}{100}$$ = 75 × $$\frac{B}{100}$$
⇒ 4A = 5B
⇒ B = $$\frac{4}{5}$$A
⇒ A × $$\frac{x}{100}$$ = B (given)
⇒ A × $$\frac{x}{100}$$ = $$\frac{4}{5}$$A
⇒ x = 80
61. The ratio of the number of boys and girls in school at 8 : 12. If 50% of boys and 25% of girls are getting scholarship for their studies, what is the percentage of school students who are not getting any scholarships ?
a) 65%
b) 66%
c) 67%
d) 68%
Explanation: Let the number of boys is = 8x
Number of girls = 12x
Boys are not getting scholarship
= 8x × $$\frac{1}{2}$$ = 4x
Girls are not getting scholarship
= 12x × $$\frac{3}{4}$$ = 9x
% of students not getting scholarship
= $$\frac{(4x + 9x)}{20x}$$ × 100
= 65%
62. In an examination there were 640 boys and 360 girls, 60% of boys and 80% of were successful. The percentage of failure was :
a) 20%
b) 30%
c) 30.5%
d) 32.8%
Explanain : The number of failure boys
= $$\frac{640 × 40}{100}$$
= 256
The number of failure girls
= $$\frac{360 × 20}{100}$$
= 72
Percentage of failure students
= $$\frac{(72 + 256)}{640 + 360}$$
= 32.8%
63. In an election between two candidates, 75% of the voters cast their votes, out of which 2% votes were declared invalid. A candidate got 9261 votes which were 75% of the valid votes. The total number of voters enrolled in that election was :
a) 16000
b) 16400
c) 16800
d) 18000
Explanation: Total valid votes got candidates
= $$\frac{9261}{75}$$ × 100
= 12348
Let total number of votes = x
Total votes polled
= x × $$\frac{75}{100}$$
= $$\frac{75x}{100}$$
Valid votes = $$\frac{75x}{100}$$ × $$\frac{98}{100}$$
According to the question,
⇔ $$\frac{75x}{100}$$ × $$\frac{98}{100}$$ = 12348
⇔ x = 16800
Hence, total votes = 16800
64. 1 litre of water is added to 5 litres of alcohol-water solution containing 40% alcohol strength. The strength of alcohol in the new solution will be :
a) 30%
b) 33%
c) $$33\frac{2}{3}$$%
d) $$33\frac{1}{3}$$%
Explanation: 40% = $$\frac{{2\,\, \to \,\,{\text{Alcohol}}}}{{5\,\, \to \,\,{\text{Mixture}}}}$$
Water : Alcohol
3 : 2
Required percentage
= $$\frac{2}{(5 + 1)}$$ × 100
= $$\frac{2}{6}$$ × 100
= $$\frac{1}{3}$$ × 100
= $$33\frac{1}{3}$$%
65. Each side of a rectangular field is diminished by 40%. By how much percent is the area of the field diminished ?
a) 32%
b) 64%
c) 25%
d) 16%
Explanation: By using successive formula
Net decrease in area
$$\eqalign{ & = 40 + 40 - \frac{{40 \times 40}}{{100}} \cr & = 64\% \cr} $$
66. The average marks obtained in a class of 50 students is 70%. The average of first 25 is 60% and that of 24 is 80%. What is the mark obtained by the last student ?
a) 90%
b) 60%
c) 80%
d) 70%
Explanation: Total Mark obtain by all 50 student = 50 × 70 = 3500
Total mark obtain by 1st 25 student = 25 × 60 = 1500
Total mark obtain by next 24 student = 24 × 80 = 1920
Mark obtain by last student = 3500 - (1500 + 1920) = 80
i.e 80% mark obtain by last student.
67. If 50% of (P - Q) = 30% of (P + Q) and Q = x% of P, then the value of x is :
a) 30
b) 25
c) 20
d) 50
Explanation:
$$\frac{50}{100}$$(P - Q) = $$\frac{30}{100}$$(P + Q)
5P - 5Q = 3P + 3Q
2P = 8Q
P = 4Q
Put value of P in given equation
Q = P × $$\frac{x}{100}$$
Q = 4Q × $$\frac{x}{100}$$
x = 25
Hence required value of x = 25
68. If x% of a is the same as y% of b, then z% of b will be :
a) $$\frac{yz}{x}$$% of a
b) $$\frac{zx}{y}$$% of a
c) $$\frac{xy}{z}$$% of a
d) $$\frac{y}{z}$$% of a
Explanation: According to the question,
a × $$\frac{x}{100}$$ = b × $$\frac{y}{100}$$
xa = yb
⇒ b = $$\frac{xa}{y}$$
Put value of b in given equation,
z% of b = z% of $$\frac{xa}{y}$$ = $$\frac{zx}{y}$$ of a
69. A candidate who gets 20% marks in a examination fails by 30 marks but another candidate who gets 32% gets 42 marks more than the pass marks. Then the percentage of pass marks is :
a) 52%
b) 50%
c) 33%
d) 25%
Explanation: Let the maximum marks = x
According to the question,
Case (i) pass marks = $$\frac{20x}{100}$$ + 30
Case (ii) pass marks = $$\frac{32x}{100}$$ - 42
Note : Pass marks would be same in both cases.
$$\frac{20x}{100}$$ + 30 = $$\frac{32x}{100}$$ - 42
$$\frac{12x}{100}$$ = 72
x = 600
Pass marks :
= 600 × $$\frac{20}{100}$$ + 30
= 150
Required percentage :
= $$\frac{150}{600}$$ × 100
= 25%
70. A man gives 50% of his money to his son and 30% to his daughter. 80% of the rest is donate to a trust. If he is left with 16000 now, how much money did he have in the beginning ?
a) Rs. 400000
b) Rs. 40000
c) Rs. 900000
d) Rs. 800000
Explanation: x × $$\frac{20}{100}$$ × $$\frac{20}{100}$$ = 16000
x = 400000
71. A man spends a part of his monthly income and saves the rest. The ratio of his expenditure to the saving is 61 : 6. If his monthly income is Rs. 8710, the amount of his monthly savings is :
a) Rs. 870
b) Rs. 690
c) Rs. 980
d) Rs. 780
Explanation: Expense + Saving = Income
61 + 6 = 67
67 units = Rs. 8710
1 unit = $$\frac{{8710}}{{67}}$$ = 130
6 unit = Rs. 780
72. A number is increased by 15% and then decreased by 25% and the number becomes 22 less than the original number. The original number is :
a) 140
b) 160
c) 120
d) 100
Explanain : Let the number is = 100x
Now after 15% of increase = 100x + 15% of 100x = 115x
Now 25% decrease = 115x - 25% of 115x = 115x - 28.75x = 86.25x
Actual decreased = 100x - 86.25x = 13.75x
According to the question,
13.75x = 22
x = $$\frac{22}{13.75}$$
100x = $$\frac{22}{13.75}$$ × 100 = 160
∴ Original number = 160
73. What is the difference between 0.6 and 0.6% ?
a) 5.94
b) 0.594
c) 60
d) 54
Explanation: 0.6% = $$\frac{0.6}{100}$$ = 0.006
So, difference = 0.6 - 0.006 = 0.594
74. A number is decreased by 10% and the resulting number is again decreased by 20%. What is the final percentage of decrease ?
a) 25%
b) 26%
c) 27%
d) 28%
Explanation: Find decreased profit
= 10 + 20 - $$\frac{10 × 20}{100}$$
= 30 - 2
= 28%
75. In an office, 40% of the staff is female. 70% of the female staff and 50% of the male staff are married. The percentage of the unmarried staff in the office is :
a) 65%
b) 42%
c) 60%
d) 64%
Explanation: Let the total staff = 100
40% of female, i.e 40 female and 60 male
70% of female staff is married i.e. 70% of 40 female = 28
Number of unmarried female = 40 - 28 = 12
50% of male staff is married i.e 50% of 60 male = 30
Number of unmarried male = 60 - 30 = 30
Total number of unmarried staff = 12 + 30 = 42
% of unmarried staff = $$\frac{42}{100}$$ × 100 = 42
76. A's salary is 50% more than that of B. Then B's salary is less than that of A by :
a) $$50$$%
b) $$33\frac{1}{3}$$%
c) $$33\frac{1}{4}$$%
d) $$33\frac{1}{2}$$%
Explanation: Let salary of B = 100
∴ Salary of A = 100 + 50% of 100 = 150
B salary is lesser then A = 150 - 100 = 50
Required %
= $$\frac{50}{150}$$ × 100 = $$33\frac{1}{3}$$%
77. If 60% of A = 30% of B, B = 40% of C and C = x% of A, then value of x is :
a) 800%
b) 200%
c) 300%
d) 500%
Explanation: According to the question,
A : B : C
1 : 2 : 5 ( 60A = 30B)
$$\frac{A}{B}$$ = $$\frac{1}{2}$$
C = 5
A = 1
Required answer = $$\frac{5}{1}$$ × 100 = 500%
78. In an examination 70% of the candidate passed in English, 80% passed in Mathematics, 10% failed in both subjects. If 144 candidates passed in both, the total number of candidates was :
a) 125
b) 200
c) 240
d) 375
Explanation: Failed candidates in English = (100 - 70) = 30%
Failed candidates in Mathematics = (100 - 80) = 20%
Candidates who fail in both subject = 10% Candidates who only fail in English = 30 - 10 = 20%
Candidates who only fail in Mathematics = 20 - 10 = 10%
Percentage of passed students in both subject
= 100 - (Candidates who only fail in English + Candidates who only fail in Mathematics + Candidates who fail in both subject)
= 100 - (20 + 10 + 10)
= 60%
According to the question,
60% of students = 144
Total students :
= $$\frac{144}{60}$$ × 100
= 240
79. Raman's salary is increased by 5% this year. If his present salary is Rs. 1806, the last year's salary was :
a) Rs. 1720
b) Rs. 1620
c) Rs. 1520
d) Rs. 1801
Explanation: Required last year salary
= $$\frac{1806}{100 + 5}$$ × 100
= Rs. 1720
80. If 80% of A = 50% of B and B = x% of A, then the value of x is :
a) 400
b) 300
c) 160
d) 150
Explanation: 80% of A = 50% of B
⇒ $$\frac{80}{100}$$A = $$\frac{50}{100}\,$$B
⇒ 8A = 5B
⇒ A = $$\frac{5}{8}$$B
Put value of A in given equation,
B = x% of A
⇒ B = $$\frac{x}{100}$$ × $$\frac{5}{8}\,$$B
⇒ x = $$\frac{100 × 8}{5}$$
⇒ x = 160
81. A sample of 50 litres of glycerine is found to be adulterated to the extent of 20%. How much pure glycerine should be added to it so as to bring down the percentage of impurity to 5% ?
a) 155 litres
b) 150 litres
c) 150.4 litres
d) 140 litres
Explanation: Give the amount of solution = 50litres
20% of impurity in a given solution
i.e.
40 liters of glycerine and 10 liters of impurities
Now to keep the impurity 10 liters and we added glycerine to a solution to bring down impurities level 5%.
i.e. 10 is 5% of 200. So we need to added glycerine 'x' amount of glycerine to make solution of 200liters
∴ x = 200 - (40 + 10) = 150 litres of glycerine
82. A and B are two fixed points 5 cm apart and C is a point an AB such that AC is 3 cm. If the length of AC is increased by 6%, the length CB is decreased by :
a) 6%
b) 7%
c) 8%
d) 9%
Explanation :
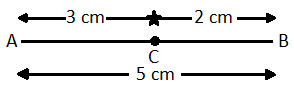
After increment of 6% new length of AC
= 3 + $$\frac{3 × 6}{100}$$ = 3.18cm
Required % decrease
= $$\frac{0.18}{2}$$ × 100
= 9%
83. What percentage of the whole week does Ajay spend in office, if his office hours are 9 am to 5 pm from Monday to Friday ?
a) 33.33%
b) 23.81%
c) 25.86%
d) 42.23%
Explanation: Time spend by Ajoy in a day = 8 hrs
Time spend by Ajay in a week = 8 × 5 = 40 hrs
Percentage time spend in a week :
= $$\frac{40}{24 × 7}$$ × 100
= 23.81%
84. A's salary was decreased by 50% and subsequently increased by 50%. How much percent does he lose ?
a) 25%
b) 30%
c) 20%
d) No loss
Explanation: Let A salary's in starting is = 100
Now after decreased by 50% A salary become = 50
Again 50% of salary increase i.e. 50% of 50 = 25
Current salary is = 50 + 25 = 75
Actual decrease in salary of A = 100 - 75 = 25
Actual % lose = $$\frac{25}{100}$$ × 100 = 25%
85. A man spend $$7\frac{1}{2}$$% of his money and after spending 75% of the remaining he had Rs. 370 left. How much money did he have :
a) 1200
b) 1600
c) 1500
d) 1400
Explanation: Let the 100unit is the salary of the person
After spending 7.5% of his salary remain salary 92.5 Now again he spended 75% of 92.5 and remain 25% which have value Rs. 370
According to the question,
92.5 × 25% unit = 370
92.5 × $$\frac{1}{4}$$ unit = 370
1 unit = $$\frac{370 × 4}{92.5}$$
100 unit = $$\frac{370 × 4 × 100}{92.5}$$
= Rs. 1600
86. There is a ratio of 5 : 4 between two numbers. If 40% of the first number is 12, then what would be 50% of the second number ?
a) 12
b) 24
c) 18
d) Data Inadequate
Explanation: 1st number : 2nd number
5 : 4
40% = $$\frac{2}{5}$$
2 units = 12
5 units = 30
So, 1st number = 30
2nd number = $$\frac{30}{5}$$ × 4 = 24
50% of 2nd = 24 × $$\frac{1}{2}$$ = 12
87. The ratio of number of boys and girls in a school 720 students is 7 : 5. How many more girls should be admitted to make the ratio 1 : 1 ?
a) 90
b) 120
c) 220
d) 240
Explanation: Number of a boy in the school = 720 × $$\frac{7}{12}$$ = 420
Number of a girl in the school = 720 × $$\frac{5}{12}$$ = 300
To maintain 1 : 1 we will have to add number of girls = 420 - 300 = 120
88. On a certain date, Pakistan has a success rate of 60% against India in all the ODI's played between the two countries. The lost the next 30 ODI's. In a row to India and their success rate comes down to 30%. The total number of ODI's played between the two countries is :
a) 50
b) 45
c) 60
d) 35
Explanation: Let a total of 5x match is played between Pakistan and India. Pakistan won 3x matches and India won 2x matches
According to the question,
But now India won 30 matches in a row and hence India's success percentage increase to 70%.
Now, Total match = 5x + 30
(2x + 30) = (5x + 30) × $$\frac{70}{100}$$
20x + 300 = 35x + 210
15x = 90
x = 6
So, total match :
= 5x + 30
= 5 × 6 + 30
= 60 matches
89. A person who spends $$66\frac{2}{3}$$% of his income is able to save Rs. 1200 per month. His monthly expenses (in Rs.) is :
a) 1200
b) 2400
c) 3000
d) 3200
Explanation:
$$66\frac{2}{3}$$% = $$\frac{2}{3}$$
Let the income of the person = 3 units
Expenditure = 2 units
Savings = (3 - 2) = 1 unit
According to the question,
1 unit = Rs. 1200
2 units = 2 × 1200 = Rs. 2400
90. The cost of an article worth Rs. 100 is increased by 10% first and again increased by 10%. The total increase in rupees is :
a) 20
b) 21
c) 110
d) 121
Explanation: % increase = 10 + 10 + $$\frac{10 × 10}{100}$$ = 21%
Total increase = $$\frac{100 × 21}{100}$$ = Rs. 21
91. One-fifth of half of a number is 20. Then 20% of that number is :
a) 80
b) 60
c) 20
d) 40
Explanation:Let the number is = x
According to the question,
$$\frac{1}{5}$$ of $$\frac{1}{2}$$ of x = 20
$$\frac{1}{5}$$ × $$\frac{1}{2}$$ × x = 20
x = 200
∴ 20% of 200 :
= $$\frac{20}{100}$$ × 200 = 40
92. In a class, the number of girls is 20% more than that of the boys. The strength of the class is 66. If 4 more girls are admitted to the class, the ratio of the number of boys to that of the girls is :
a) 1 : 2
b) 3 : 4
c) 1 : 4
d) 3 : 5
Explanain : 20% = $$\frac{1}{5}$$ = $$\frac{{6\,\, \to \,\,{\text{Girls}}}}{{5\,\, \to \,\,{\text{Boys}}}}$$
Boys : Girls
5 : 6
According to the question,
(5 + 6) units = 66
11 units = 66
1 unit = 6
Hence Boys = 6 × 5 = 30
Girls = 6 × 6 = 36
The number of girls when 4 is admitted
= (36 + 4)
= 40
Required ratio :
= 30 : 40
= 3 : 4
93. If P% of P is 36, then P is equal to :
a) 3600
b) 600
c) 60
d) 15
Explanation: According to the question,
P × $$\frac{P}{100}$$ = 36
⇒ P2 = 3600
⇒ P = 60
94. If A is equal to 20% of B and B is equal to 25% of C. Then what percentage of C equal to A ?
a) 10%
b) 15%
c) 5%
d) 20%
Explanation: A = 20% of B
A = $$\frac{1}{5}$$ B
$$\frac{A}{B} = \frac{1}{5}$$ ----(i)
B = 25% of C
B = $$\frac{1}{4}$$ C
$$\frac{B}{C} = \frac{1}{4}$$ ----(ii)
Multiply (i) and (ii) We get
$$\frac{A}{B} \times \frac{B}{C} = \frac{1}{5} \times \frac{1}{4}$$
$$\frac{A}{C} = \frac{1}{{20}}$$
Percent of C is equal to A
$$ = \frac{1}{{20}} \times 100 = 5\% $$
95. The marked price of an article is Rs. 5000 but due to festive offer a certain percent of discount is declared. Mr. x availed this opportunity and bought the article at reduced price. He then sold it at Rs. 5000 and thereby made a profit of $$11\frac{1}{9}$$%. The percentage of discount allowed was ?
a) 10%
b) $$3\frac{1}{3}$$%
c) $$7\frac{1}{2}$$%
d) $$11\frac{1}{9}$$%
Explanation: We find a percentage value of so we take or not take real value does not matters
% Profit = $$11\frac{1}{9}$$% = $$\frac{1}{9}$$
$$\frac{{1\,\, \to \,\,{\text{Profit}}}}{{2\,\, \to \,\,{\text{CP}}}}$$
So, SP = 10
Means in previous at the time of beginning the discount is 1 unit in 10 units MP
So, discount is = $$\frac{1}{10}$$ × 100 = 10%
96. The price of an article was first increased by 10% and then again by 20%. If the last increased price was Rs. 33, the original price was :
a) Rs. 30
b) Rs. 27.50
c) Rs. 26.50
d) Rs. 25
Explanation: Let the original price = 100x
Article price 1st increased by 10%. i.e price of article become 100x + 100x of 10% = 110x
And then the article price increased by 20% i.e. price of article become 110x + 110x of 20% = 132x
According to the question,
132x = 33
⇒ x = $$\frac{33}{132}$$
⇒ x = $$\frac{1}{4}$$
Therefore Original price of Article is
= 100 × $$\frac{1}{4}$$
= Rs. 25
97. The price of a commodity rises from Rs. 6 per kg to Rs. 7.50 per kg. If the expenditure cannot increase, the percentage of reduction in consumption is :
a) 15%
b) 20%
c) 25%
d) 30%
Explanation: Gain in price = 7.5 - 6 = 1.5
Required percentage reduction
= $$\frac{1.5}{7.5}$$ × 100
= 20%
98. What % of a day is 30 minutes ?
a) 2.83
b) 2.083
c) 2.09
d) 2.075
Explanation: Required %
= $$\frac{30}{24 × 60}$$ × 100
= 2.083
99. A scored 72% in a paper with a maximum marks of 900 and 80% in another paper with a maximum marks of 700. If the result is based on the combined percentage of two papers, the combined percentage is :
a) 75.5%
b) 76%
c) 76.5%
d) 77%
Explanation:900 × 72% = 648
700 × 80% = 560
Total scored marks = 1208
= % combined marks
= $$\frac{1208}{(900 + 700)}$$ × 100
= 75.5%
100. In an examination a candidate must secure 40% marks to pass. A candidate, who gets 220 marks, fails by 20 marks. Find the maximum marks for the examination ?
a) 1200
b) 300
c) 600
d) 450
Explanation: According to the question,
Pass marks = (220 + 20) = 240
40% → 240
∴ Maximum marks (100%) :
= $$\frac{240}{40}$$ × 100
= 600