1. In a class of 60 students, the number of boys and girls participating in the annual sports is in the ratio 3 : 2 respectively. The number of girls not participating in the sports is 5 more than the number of boys not participating in the sports. If the number of boys participating in the sports is 15, then how many girls are there in the class ?
a) 20
b) 25
c) 30
d) None of these
Explanation: Let the number of boys and girls participating in sports be 3x and 2x respectively.
Then, 3x = 15 or x = 5.
So, number of girls participating in sports = 2x = 10.
Number of students not participating in sports = 60 - (15 + 10) = 35.
Let number of boys not participating in sports be y.
Then, number of girls not participating in sports = (35 -y).
Therefore (35 - y) = y + 5 ⇔ 2y ⇔ 30 ⇔ y = 15.
So, number of girls not participating in sports = (35 - 15) = 20.
Hence, total number of girls in the class = (10 + 20) = 30.
2. There are deer and peacocks in a zoo. By counting heads they are 80. The number of their legs is 200. How many peacocks are there ?
a) 20
b) 30
c) 50
d) 60
Explanation: Let x and y be the number of deer and peacocks in the zoo respectively. Then,
x + y = 80 ...(i) and
4x + 2y = 200 or 2x + y = 100 ...(ii)
Solving (i) and (ii), we get) x = 20, y = 60.
3. A man wears socks of two colours - Black and brown. He has altogether 20 black socks and 20 brown socks in a drawer. Supposing he has to take out the socks in the dark, how many must he take out to be sure that he has a matching pair ?
a) 3
b) 20
c) 39
d) None of these
Explanation: Since there are socks of only two colours, so two out of any three socks must always be of the same colour.
4. A motorist knows four different routes from Bristol to Birmingham. From Birmingham to Sheffield he knows three different routes and from Sheffield to Carlisle he knows two different routes. How many routes does he know from Bristol to Carlisle ?
a) 4
b) 8
c) 12
d) 24
Explanation: Total number of routes from Bristol to Carlisle = (4 x 3 x 2) = 24.
5. Mac has £ 3 more than Ken, but then Ken wins on the horses and trebles his money, so that he now has £ 2 more than the original amount of money that the two boys had between them. How much money did Mac and Ken have between them before Ken's win ?
a) £ 9
b) £ 11
c) £ 13
d) £ 15
Explanation: Let money with Ken = x. Then, money with Mac = x + £ 3.
Now, 3x = (x + x + £ 3) + £ 2 ⇔ x = £ 5.
Therefore Total money with Mac and Ken = 2x + £ 3 = £ 13.
6. The total of the ages of Amar, Akbar and Anthony is 80 years. What was the total of their ages three years ago ?
a) 71 years
b) 72 years
c) 74 years
d) 77 years
Explanation: Required sum = (80 - 3 x 3) years = (80 - 9) years = 71 years.
7. Two bus tickets from city A to B and three tickets from city A to C cost Rs. 77 but three tickets from city A to B and two tickets from city A to C cost Rs. 73. What are the fares for cities B and C from A ?
a) Rs. 4, Rs. 23
b) Rs. 13, Rs. 17
c) Rs. 15, Rs. 14
d) Rs. 17, Rs. 13
Explanation: Let Rs. x be the fare of city B from city A and Rs. y be the fare of city C from city A.
Then, 2x + 3y = 77 ...(i) and
3x + 2y = 73 ...(ii)
Multiplying (i) by 3 and (ii) by 2 and subtracting, we get: 5y = 85 or y = 17.
Putting y = 17 in (i), we get: x = 13.
8. An institute organised a fete and 1/5 of the girls and 1/8 of the boys participated in the same. What fraction of the total number of students took part in the fete ?
a) 2/13
b) 13/40
c) Data inadequate
d) None of these
Explanation: Data inadequate
9. A number of friends decided to go on a picnic and planned to spend Rs. 96 on eatables. Four of them, however, did not turn up. As a consequence, the remaining ones had to contribute Rs. 4 each extra. The number of those who attended the picnic was
a) 8
b) 12
c) 16
d) 24
Explanation:

10. A, B, C, D and E play a game of cards. A says to B, "If you give me three cards, you will have as many as E has and if I give you three cards, you will have as many as D has." A and B together have 10 cards more than what D and E together have. If B has two cards more than what C has and the total number of cards be 133, how many cards does B have ?
a) 22
b) 23
c) 25
d) 35
Explanation: Clearly, we have :
B - 3 = E ...(i)
B + 3 = D ...(ii)
A+B = D + E+10 ...(iii)
B = C + 2 ...(iv)
A+B + C + D + E= 133 ...(v)
From (i) and (ii), we have : 2 B = D + E ...(vi)
From (iii) and (vi), we have : A = B + 10 ...(vii)
Using (iv), (vi) and (vii) in (v), we get:
(B + 10) + B + (B - 2) + 2B = 133 ⇔ 5B = 125 ⇔ B = 25.
11. A is three times as old as B. C was twice-as old as A four years ago. In four years' time, A will be 31. What are the present ages of B and C ?
a) 9, 46
b) 9, 50
c) 10, 46
d) 10, 50
Explanation: We have : A = 3B ...(i) and
C - 4 = 2 (A - 4) ...(ii)
Also, A + 4 = 31 or A= 31-4 = 27.
Putting A = 27 in (i), we get: B = 9.
Putting A = 27 in (ii), we get C = 50.
12. Today is Varun's birthday. One year, from today he will be twice as old as he was 12 years ago. How old is Varun today ?
a) 20 years
b) 22 years
c) 25 years
d) 27 years
Explanation:Let Varan's age today = x years.
Then, Varan's age after 1 year = (x + 1) years.
Therefore x + 1 = 2 (x - 12) ⇔ x + 1 = 2x - 24 ⇔ x = 25.
13. A bird shooter was asked how many birds he had in the bag. He replied that there were all sparrows but six, all pigeons but six, and all ducks but six. How many birds he had in the bag in all?
a) 9
b) 18
c) 27
d) 36
Explanation: There were all sparrows but six' means that six birds were not sparrows but only pigeons and ducks.
Similarly, number of sparrows + number of ducks = 6 and number of sparrows + number of pigeons = 6.
This is possible when there are 3 sparrows, 3 pigeons and 3 ducks i.e. 9 birds in all.
14. Mr. Johnson was to earn £ 300 and a free holiday for seven weeks' work. He worked for only 4 weeks and earned £ 30 and a free holiday. What was the value of the holiday?
a) £ 300
b) £ 330
c) £ 360
d) £ 420
Explanation:
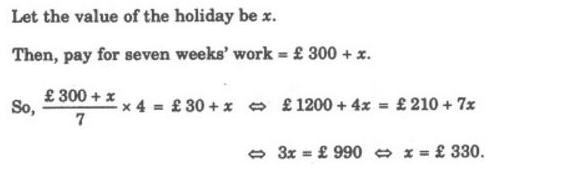
15. What is the smallest number of ducks that could swim in this formation - two ducks in front of a duck, two ducks behind a duck and a duck between two ducks ?
a) 3
b) 5
c) 7
d) 9
Explanation: Clearly, the smallest such number is 3.

Three ducks can be arranged as shown above to satisfy all the three given conditions.
16. A fires 5 shots to B's 3 but A kills only once in 3 shots while B kills once in 2 shots. When B has missed 27 times, A has killed
a) 30 birds
b) 60 birds
c) 72 birds
d) 90 birds
Explanation:

17. In a class, 3/5 of the students are girls and rest are boys. If 2/9 of the girls and 1/4 of the boys are absent, what part of the total number of students is present ?
a) 17/25
b) 18/49
c) 23/30
d) 23/36
Explanation:

18. In a family, a couple has a son and a daughter. The age of the father is three times that of his daughter and the age of the son is half of that of his mother. The wife is 9 years younger to her husband and the brother is seven years older than his sister. What is the age of the mother ?
a) 40 years
b) 45 years
c) 50 years
d) 60 years
Explanation: Let the daughter's age be x years.
Then, father's age = (3x) years.
Mother's age = (3x - 9) years; Son's age = (x + 7) years.
So, x + 7 = (3x-9)/2 ⇔ 2x + 14 = 3x - 9 ⇔ x = 23.
Therefore Mother's age = (3X - 9) = (69 - 9) years = 60 years.
19. If a 1 mm thick paper is folded so that the area is halved at every fold, then what would be the thickness of the pile after 50 folds ?
a) 100 km
b) 1000 km
c) 1 million km
d) 1 billion km
Explanation:

20. First bunch of bananas has (1/4) again as many bananas as a second bunch. If the second bunch has 3 bananas less than the first bunch, then the number of bananas in the first bunch is
a) 9
b) 10
c) 12
d) 15
Explanation:

21. Five bells begin to toll together and toll respectively at intervals of 6, 5, 7, 10 and 12 seconds. How many times will they toll together in one hour excluding the one at the start ?
a) 7 times
b) 8 times
c) 9 times
d) 11 times
Explanation: L.C.M. of 6, 5, 7, 10 and 12 is 420.
So, the bells will toll together after every 420 seconds i.e. 7 minutes.
Now, 7 x 8 = 56 and 7 x 9 = 63.
Thus, in 1-hour (or 60 minutes), the bells will toll together 8 times, excluding the one at the start.
22. A bus starts from city X. The number of women in the bus is half of the number of men. In city Y, 10 men leave the bus and five women enter. Now, number of men and women is equal. In the beginning, how many passengers entered the bus ?
a) 15
b) 30
c) 36
d) 45
Explanation: Originally, let number of women = x. Then, number of men = 2x.
So, in city Y, we have : (2x - 10) = (x + 5) or x - 15.
Therefore Total number of passengers in the beginning = (x + 2x) = 3x = 45.
23. A, B, C, D and E play a game of cards. A says to B, "If you give me 3 cards, you will have as many as I have at this moment while if D takes 5 cards from you, he will have as many as E has." A and C together have twice as many cards as E has. B and D together also have the same number of cards as A and C taken together. If together they have 150 cards, how many cards has C got
a) 28
b) 29
c) 31
d) 35
Explanation: Clearly, we have :
A = B - 3 ...(i)
D + 5 = E ...(ii)
A+C = 2E ...(iii)
B + D = A+C = 2E ...(iv)
A+B + C + D + E=150 ...(v)
From (iii), (iv) and (v), we get: 5E = 150 or E = 30.
Putting E = 30 in (ii), we get: D = 25.
Putting E = 30 and D = 25 in (iv), we get: B = 35.
Putting B = 35 in (i), we get: A = 32.
Putting A = 32 and E = 30 in (iii), we get: C = 28.
24. A farmer built a fence around his square plot. He used 27 fence poles on each side of the square. How many poles did he need altogether ?
a) 100
b) 104
c) 108
d) None of these
Explanation: Since each pole at the corner of the plot is common to its two sides, so we have :
Total number of poles needed = 27 x 4 - 4 = 108 - 4 = 104.
25. In a city, 40% of the adults are illiterate while 85% of the children are literate. If the ratio of the adults to that of the children is 2 : 3, then what percent of the population is literate ?
a) 20%
b) 25%
c) 50%
d) 75%
Explanation:

26. The number of boys in a class is three times the number of girls. Which one of the following numbers cannot represent the total number of children in the class ?
a) 48
b) 44
c) 42
d) 40
Explanation: Let number of girls = x and number of boys = 3x.
Then, 3x + x = 4x = total number of students.
Thus, to find exact value of x, the total number of students must be divisible by 4.
27. A shepherd had 17 sheep. All but nine died. How many was he left with ?
a) Nil
b) 8
c) 9
d) 17
Explanation: 'All but nine died' means 'All except nine died' i.e. 9 sheep remained alive
28. In a family, the father took 1/4 of the cake and he had 3 times as much as each of the other members had. The total number of family members is
a) 3
b) 7
c) 10
d) 12
Explanation:

29. In three coloured boxes - Red, Green and Blue, 108 balls are placed. There are twice as many balls in the green and red boxes combined as there are in the blue box and twice as many in the blue box as there are in the red box. How many balls are there in the green box ?
a) 18
b) 36
c) 45
d) None of these
Explanation: Let R, G and B represent the number of balls in red, green and blue boxes respectively.
Then, .
R + G + B = 108 ...(i),
G + R = 2B ...(ii)
B = 2R ...(iii)
From (ii) and (iii), we have G + R = 2x 2R = 4R or G = 3R.
Putting G = 3R and B = 2R in (i), we get:
R + 3R + 2R = 108 ⇔ 6R = 108 ⇔ R = 18.
Therefore Number of balls in green box = G = 3R = (3 x 18) = 54.
30. In a cricket match, five batsmen A, B, C, D and E scored an average of 36 runs. D Scored 5 more than E; E scored 8 fewer than A; B scored as many as D and E combined; and B and C scored 107 between them. How many runs did E score ?
a) 62
b) 45
c) 28
d) 20
Explanation: otal runs scored = (36 x 5) = 180.
Let the runs scored by E be x.
Then, runs scored by D = x + 5; runs scored by A = x + 8;
runs scored by B = x + x + 5 = 2x + 5;
runs scored by C = (107 - B) = 107 - (2x + 5) = 102 - 2x.
So, total runs = (x + 8) + (2x + 5) + (102 - 2x) + (x + 5) + x = 3x + 120.
Therefore 3x + 120 =180 ⇔ 3X = 60 ⇔ x = 20.