a) 12 m
b) 10 m
c) 8 m
d) 6 m

Answer: a
Explanation: Let AB and CD be two poles
AB = 20 m, CD = 14 m
A and C are joined by a wire
CE || DB and angle of elevation of A is 30°
Let CE = DB = x and AC = L

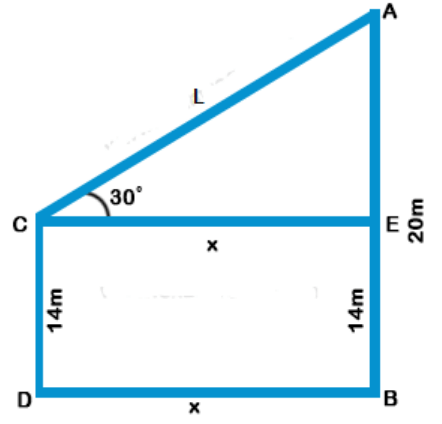
Now AE = AB – EB = AB – CD = 20 – 14 = 6 m
$$\eqalign{ & {\text{Now in right }}\Delta ACE, \cr & \sin \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} = \frac{{AE}}{{AC}} \cr & \sin {30^ \circ } = \frac{6}{{AC}} \cr & \frac{1}{2} = \frac{6}{{AC}} \cr & \Rightarrow AC = 2 \times 6 = 12 \cr & {\text{Length of AC}} = 12\,m \cr} $$