a) $$\left( {\sqrt 3 + 1} \right)\,x$$
b) $$\left( {\sqrt 3 – 1} \right)\,x$$
c) $$2\sqrt 3 \,x$$
d) $$3\sqrt 2 \,x$$

Answer: a
Explanation: AB is a tower
BD and BC are its shadows and CD = 2x

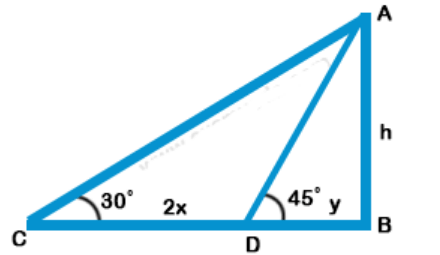
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{DB}} \cr & \Rightarrow 1 = \frac{h}{y} \Rightarrow y = h \cr & {\text{and}}\tan {30^ \circ } = \frac{{AB}}{{CB}} \cr & \frac{1}{{\sqrt 3 }} = \frac{h}{{2x + y}} \cr & 2x + y = \sqrt 3 \,h \cr & \sqrt 3 \,h – h = 2x \cr & h\left( {\sqrt 3 – 1} \right) = 2x \cr & \Rightarrow h = \frac{{2x}}{{\sqrt 3 – 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 – 1} \right)\left( {\sqrt 3 + 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{{3 – 1}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{2x\left( {\sqrt 3 + 1} \right)}}{2} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = x\left( {\sqrt 3 + 1} \right) \cr} $$