The angle of elevation of the top of a tower standing on a horizontal plane from a point A is α. After walking a distance ‘d’ towards the foot of the tower the angle of elevation is found to be β. The height of the tower is:
a) $$\frac{d}{{\cot \alpha + \cot \beta }}$$
b) $$\frac{d}{{\cot \alpha – \cot \beta }}$$
c) $$\frac{d}{{\tan \beta – \operatorname{tant} \alpha }}$$
d) $$\frac{d}{{\tan \beta + \operatorname{tant} \alpha }}$$

Answer: b
Explanation: Let AB be the tower and C is a point such that the angle of elevation of A is α.
After walking towards the foot B of the tower, at D the angle of elevation is β.
Let h be the height of the tower and DB = x Now in ΔACB,

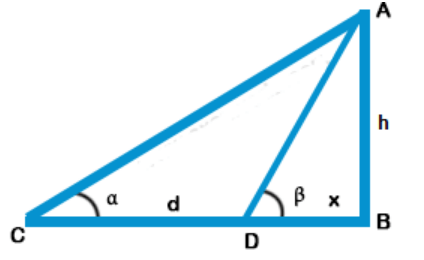
$$\eqalign{ & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{CB}} \cr & \tan \alpha = \frac{h}{{d + x}} \cr & \Rightarrow d + x = \frac{h}{{\tan \alpha }} \cr & \Rightarrow d + x = h\cot \alpha \cr & \Rightarrow x = h\cot \alpha – d\,…….\left( {\text{i}} \right) \cr & {\text{Similarly in right }}\Delta ADB, \cr & \tan \beta = \frac{h}{x} \cr & \Rightarrow x = \frac{h}{{\tan \beta }} \cr & \Rightarrow x = h\cot \beta \,………({\text{ii}}) \cr & {\text{From}}\,\left( {\text{i}} \right)\,{\text{and}}\,\left( {{\text{ii}}} \right) \cr & h\cot \alpha – d = h\cot \beta \cr & h\cot \alpha – h\cot \beta = d \cr & h\left( {\cot \alpha – \cot \beta } \right) = d \cr & h = \frac{d}{{\cot \alpha – \cot \beta }} \cr} $$
Height of the tower $$ = \frac{d}{{\cot \alpha – \cot \beta }}$$