a) $$\frac{{240\sqrt 3 }}{{\sqrt 3 – 1}}\,{\text{ft}}$$
b) $$\frac{{240}}{{\sqrt 3 – 1}}\,{\text{ft}}$$
c) $$\frac{{240}}{{\sqrt 3 }}\,{\text{ft}}$$
d) $$240\sqrt 3 \,{\text{ft}}$$

Answer: a
Explanation:

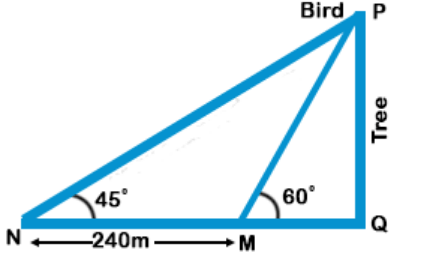
$$\eqalign{ & {\text{Now,}}\,{\text{tan}}{45^ \circ } = 1 = \frac{{PQ}}{{NQ}} \cr & {\text{Tree}}\,{\text{height}} \cr & = PQ = NQ \cr & = \left( {240 + MQ} \right) \cr & \tan {60^ \circ } = \sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{PQ}}{{MQ}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240 + MQ}}{{MQ}} \cr & 240 + MQ = \sqrt 3 \,MQ \cr & MQ = \frac{{240}}{{\sqrt 3 – 1}}\,{\text{ft}} \cr & NQ = 240 + MQ \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{240\sqrt 3 }}{{\sqrt 3 – 1}}\,{\text{ft}} \cr} $$
= Rohit was this much far away initially