a) 272 m
b) 284 m
c) 288 m
d) 254 m

Answer: d
Explanation:

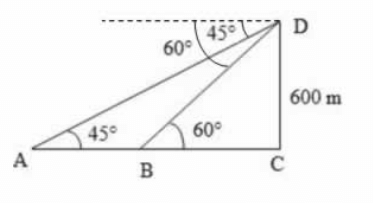
Let DC be the tower and A and B be the objects as shown above.
Given that DC = 600 m, ∠DAC = 45°, ∠DBC = 60°
$$\eqalign{ & \tan {60^ \circ } = \frac{{DC}}{{BC}} \cr & \sqrt 3 = \frac{{600}}{{BC}} \cr & BC = \frac{{600}}{{\sqrt 3 }}\,……….\,\left( {\text{i}} \right) \cr & \tan {45^ \circ } = \frac{{DC}}{{AC}} \cr & 1 = \frac{{600}}{{AC}} \cr & AC = 600\,…………\,\left( {{\text{ii}}} \right) \cr} $$
Distance between the objects
$$ = AC = \left( {AC – BC} \right)$$
$$ = 600 – \frac{{600}}{{\sqrt 3 }}$$   [ from (1) and (ii)]
$$\eqalign{ & = 600\left( {1 – \frac{1}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 – 1}}{{\sqrt 3 }}} \right) \cr & = 600\left( {\frac{{\sqrt 3 – 1}}{{\sqrt 3 }}} \right) \times \frac{{\sqrt 3 }}{{\sqrt 3 }} \cr & = \frac{{600\sqrt 3 \left( {\sqrt 3 – 1} \right)}}{3} \cr & = 200\sqrt 3 \left( {\sqrt 3 – 1} \right) \cr & = 200\left( {3 – \sqrt 3 } \right) \cr & = 200\left( {3 – 1.73} \right) \cr & = 254\,m \cr} $$