a) 40 m
b) 138.4 m
c) 46.24 m
d) 160 m

Answer: b
Explanation:

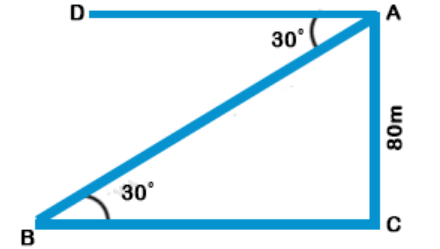
Let AC be the tower and B be the position of the bus.
Then BC = the distance of the bus from the foot of the tower.
Given that height of the tower, AC = 80 m and the angle of depression, ∠DAB = 30°
∠ABC = ∠DAB = 30° (because DA || BC)
$$\eqalign{ & \tan {30^ \circ } = \frac{{AC}}{{BC}} \cr & \tan {30^ \circ } = \frac{{80}}{{BC}} \cr & BC = \frac{{80}}{{\tan {{30}^ \circ }}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{80}}{{\left( {\frac{1}{{\sqrt 3 }}} \right)}} \cr & = 80 \times 1.73 = 138.4\,{\text{m}} \cr} $$
i.e., Distance of the bus from the foot of the tower = 138.4 m