a) 32 kmph
b) 36 kmph
c) 38 kmph
d) 40 kmph

Answer: a
Explanation:

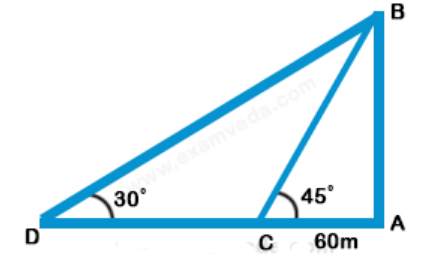
Let AB be the tower and C and D be the two positions of the boats.
Then, $$\angle {\text{ACB = }}{45^ \circ },$$    $$\angle ADB = {30^ \circ }$$     and AC = 60 m
Let, AB = h
$$\eqalign{ & {\text{Then,}}\frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow AB = AC \cr & \Rightarrow h = 60\,m \cr & {\text{And}}\frac{{AB}}{{AD}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & AD = \left( {AB \times \sqrt 3 } \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 60\sqrt 3 \,m \cr & CD = \left( {AD – AC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = 60\left( {\sqrt 3 – 1} \right)\,m \cr & {\text{Hence, required speed }} \cr & {\text{ = }}\left[ {\frac{{60\left( {\sqrt 3 – 1} \right)}}{5}} \right]{\text{m/s}} \cr & {\text{ = }}\left( {12 \times 0.73} \right){\text{m/s}} \cr & = \left( {12 \times 0.73 \times \frac{{18}}{5}} \right){\text{km/hr}} \cr & = {\text{31}}{\text{.5km/hr }} \approx {\text{ 32km/hr}} \cr} $$