a) 45 m
b) 30 m
c) 103.8 m
d) 94.6 m

Answer: d
Explanation:

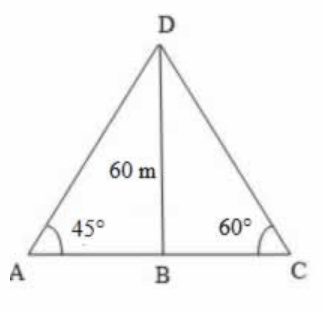
Let BD be the lighthouse and A and C be the two points on ground.
Then, BD, the height of the lighthouse = 60 m
∠BAD = 45°, ∠BCD = 60°
$$\eqalign{ & \tan {45^ \circ } = \frac{{BD}}{{BA}} \cr & 1 = \frac{{60}}{{BA}} \cr & BA = 60\,m\,……..\left( {\text{i}} \right) \cr & \tan {60^ \circ } = \frac{{BD}}{{BC}} \cr & \sqrt 3 = \frac{{60}}{{BC}} \cr & \Rightarrow BC = \frac{{60}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{60\sqrt 3 }}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20\sqrt 3 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 20 \times 1.73 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 34.6\,m\,……….\left( {{\text{ii}}} \right) \cr} $$
Distance between the two points A and C
= AC = BA + BC
= 60 + 34.6 [ Substituted value of BA and BC from (i) and (ii)]
= 94.6 m